
من أنا
اسمي ديمتري إيفانوف. أنا طالب دراسات عليا في السنة الثانية في الاقتصاد في HSE في سانت بطرسبرغ. أعمل في مجموعة البحث " Agent Systems and Reinforcement Learning " في JetBrains Research ، وكذلك في المختبر الدولي لنظرية الألعاب وصنع القرار في المدرسة العليا للاقتصاد . بالإضافة إلى تعلم PU ، أنا مهتم بالتعلم المعزز والبحث عند تقاطع التعلم الآلي والاقتصاد.
الديباجة
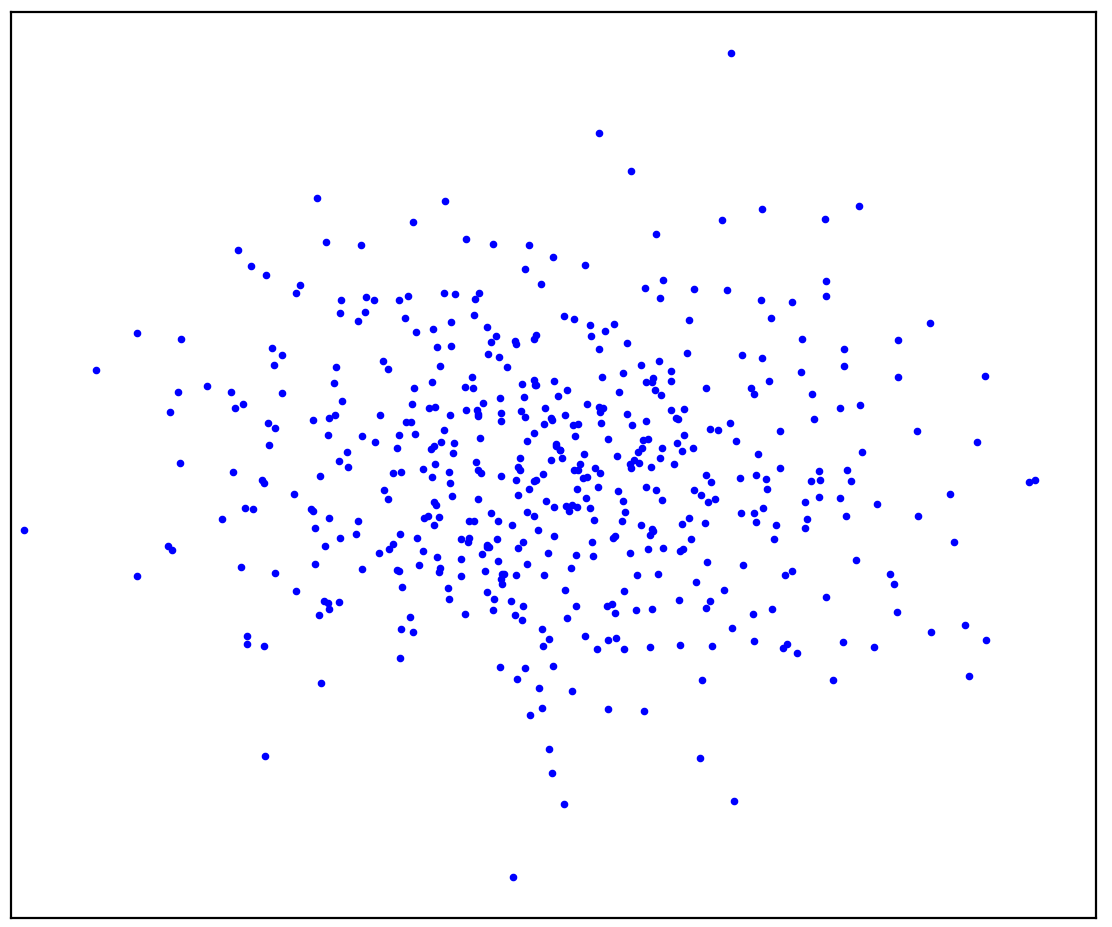
الشكل: 1 أ. البيانات الإيجابية
يوضح الشكل 1 أ مجموعة من النقاط الناتجة عن بعض التوزيعات ، والتي سنسميها إيجابية. سيتم تسمية جميع النقاط المحتملة الأخرى التي لا تنتمي إلى التوزيع الإيجابي بالنفي. حاول أن ترسم خطًا عقليًا يفصل بين النقاط الإيجابية المقدمة من جميع النقاط السلبية المحتملة. بالمناسبة ، هذه المهمة تسمى "كشف الشذوذ".
الجواب هنا

. 1.

. 1.
ربما تخيلت شيئًا مثل الشكل 1 ب: وضع دائرة حول البيانات في قطع ناقص. في الواقع ، هذا هو عدد طرق اكتشاف العيوب التي تعمل.
دعونا الآن نغير المشكلة قليلاً: لنحصل على معلومات إضافية مفادها أن الخط المستقيم يجب أن يفصل النقاط الإيجابية عن السالبة. حاول أن ترسمه في ذهنك.
الجواب هنا
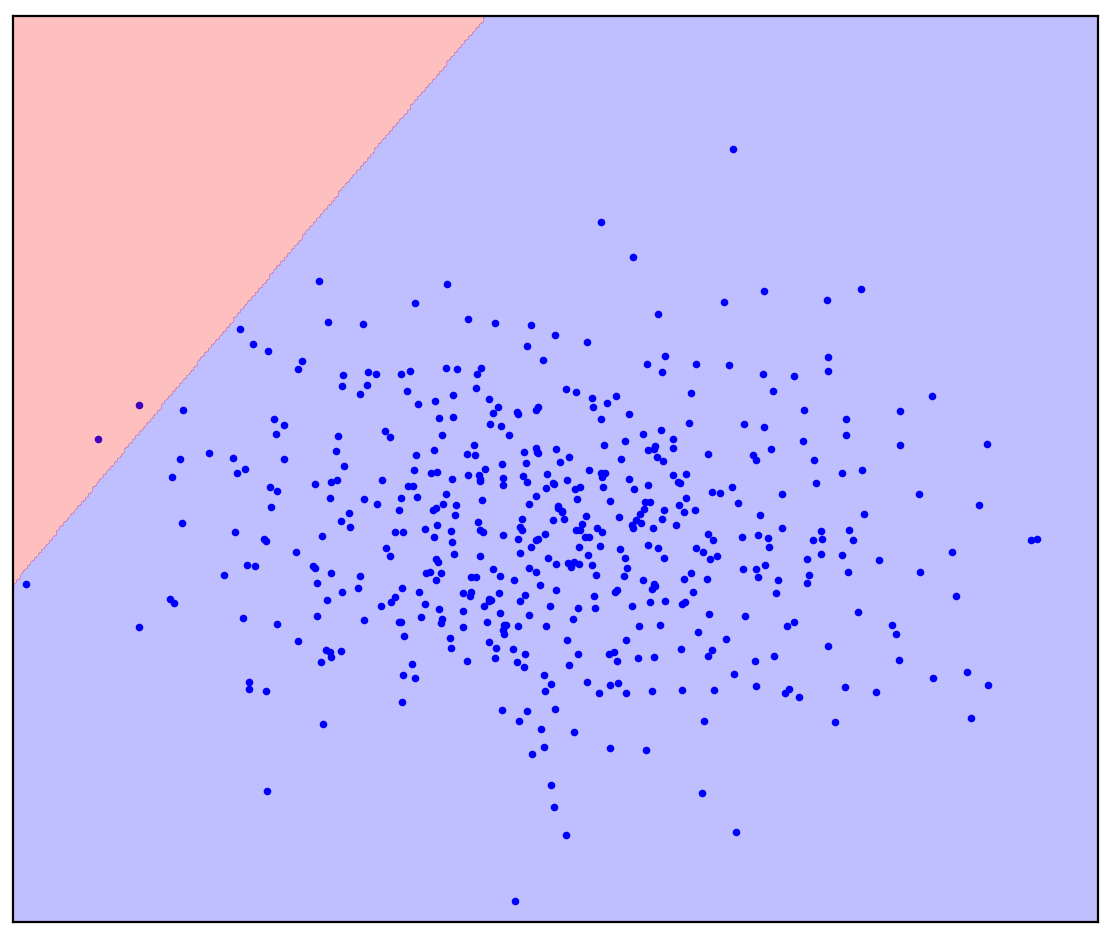
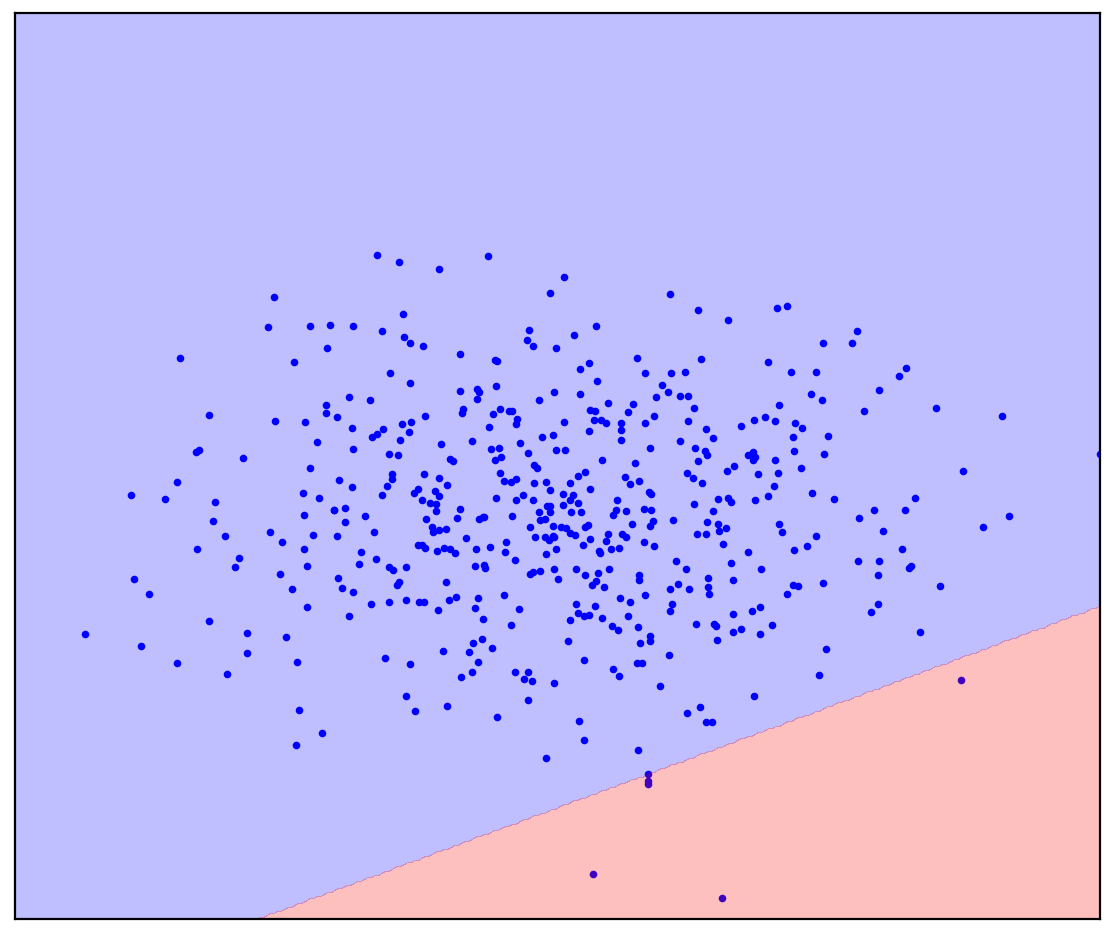
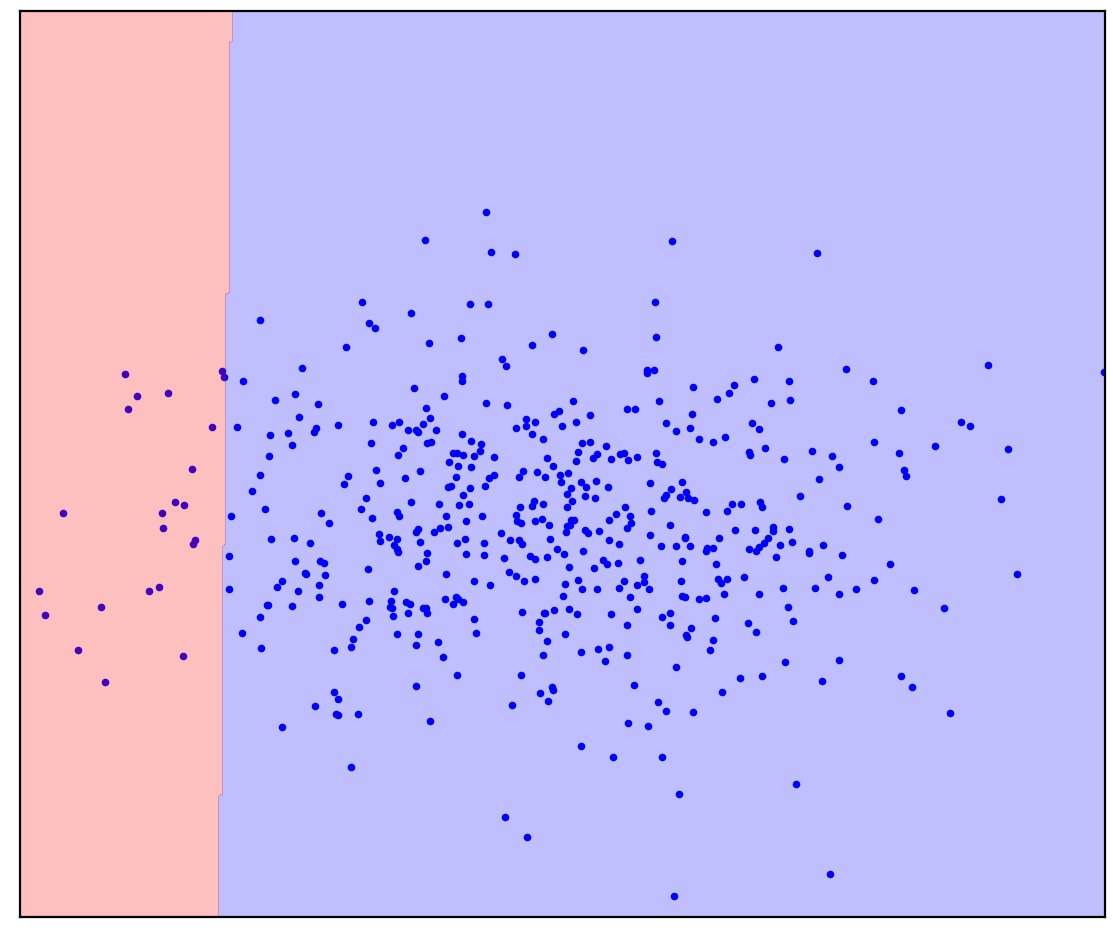
. 1. ( One-Class SVM)



. 1. ( One-Class SVM)
في حالة وجود خط فاصل مستقيم ، لا توجد إجابة واحدة. ليس من الواضح في أي اتجاه لرسم خط مستقيم.
الآن سأضيف بعض النقاط غير المخصصة إلى الشكل 1 د والتي تحتوي على مزيج من الإيجابية والسلبية. للمرة الأخيرة ، سأطلب منك بذل مجهود ذهني وتخيل خط يفصل بين النقاط الإيجابية والسلبية. لكن هذه المرة يمكنك استخدام البيانات غير المسماة!

الشكل: 1 د. نقاط موجبة (زرقاء) وغير مسماة (حمراء). تتكون النقاط غير المميزة من إيجابية وسلبية
الجواب هنا

. 1.

. 1.
أصبح الأمر أسهل! على الرغم من أننا لا نعرف مسبقًا كيف يتم إنشاء كل نقطة معينة غير محددة ، يمكننا تحديدها تقريبًا من خلال مقارنتها بالنقاط الإيجابية. من المحتمل أن تكون النقاط الحمراء التي تبدو زرقاء اللون إيجابية. على العكس من ذلك ، ربما تكون العناصر غير المتشابهة سلبية. نتيجة لذلك ، على الرغم من حقيقة أنه ليس لدينا بيانات سلبية "خالصة" ، يمكن الحصول على معلومات عنها من الخليط غير المصنف واستخدامها لتصنيف أكثر دقة. هذا ما تفعله خوارزميات التعلم الإيجابي غير المصنف ، والذي أريد التحدث عنه.
المقدمة
يمكن ترجمة التعلم الإيجابي غير المصنف (PU) على أنه "التعلم من البيانات الإيجابية وغير المصنفة". في الواقع ، يعد تعلم PU نظيرًا لتصنيف ثنائي للحالات عندما يكون هناك بيانات مصنفة لواحد فقط من الفئات ، ولكن يتوفر مزيج غير مصنف من البيانات من كلا الفئتين. في الحالة العامة ، لا نعرف حتى مقدار البيانات الموجودة في الخليط التي تتوافق مع فئة موجبة ومقدار فئة سلبية. بناءً على مجموعات البيانات هذه ، نريد إنشاء مصنف ثنائي: كما هو الحال في وجود بيانات نقية لكلا الفئتين.
كمثال على لعبة ، ضع في اعتبارك مصنفًا لصور القطط والكلاب. لدينا بعض صور القطط والعديد من الصور لكل من القطط والكلاب. عند الإخراج ، نريد الحصول على مصنف: وظيفة تتنبأ باحتمال تصوير قطة لكل صورة. في الوقت نفسه ، يمكن للمصنف تمييز خليطنا الحالي من صور القطط والكلاب. في الوقت نفسه ، قد يكون من الصعب / المكلف / تستغرق وقتًا طويلاً / من المستحيل ترميز الصور يدويًا لتدريب المصنف ، فأنت تريد القيام بذلك بدونها.
تعلم PU هو مهمة طبيعية جدا. غالبًا ما تكون البيانات الموجودة في العالم الحقيقي قذرة. تبدو القدرة على التعلم من البيانات القذرة بمثابة اختراق مفيد للحياة بجودة عالية نسبيًا. على الرغم من ذلك ، فقد قابلت ، على سبيل المفارقة ، عددًا قليلاً من الأشخاص الذين سمعوا عن تعلم اللغة الإنجليزية ، وعدد أقل ممن كانوا يعرفون عن أي طرق محددة. لذلك قررت أن أتحدث عن هذا المجال.

الشكل: 2. Jürgen Schmidhuber and Yann LeCun، NeurIPS 2020
تطبيق التعلم بو
سوف أقسم بشكل غير رسمي الحالات التي يمكن أن يكون فيها تعلم اللغة الإنجليزية مفيدًا إلى ثلاث فئات. ربما تكون
الفئة الأولى هي الأكثر وضوحًا: يمكن استخدام تعلم PU بدلاً من التصنيف الثنائي المعتاد. في بعض المهام ، تكون البيانات بطبيعتها متسخة قليلاً. من حيث المبدأ ، يمكن تجاهل هذا التلوث ويمكن استخدام مصنف تقليدي. ولكن من الممكن تغيير القليل جدًا من وظيفة الخسارة عند تدريب المصنف (Kiryo et al. ، 2017) أو حتى التنبؤات نفسها بعد التدريب (Elkan & Noto ، 2008) ، ويصبح التصنيف أكثر دقة.
كمثال ، ضع في اعتبارك تحديد الجينات الجديدة المسؤولة عن تطوير جينات المرض. النهج القياسي هو علاج جينات المرض التي تم العثور عليها بالفعل على أنها إيجابية وجميع الجينات الأخرى سلبية. من الواضح أن جينات المرض التي لم يتم العثور عليها بعد قد تكون موجودة في هذه البيانات السلبية. علاوة على ذلك ، فإن المهمة نفسها هي البحث عن جينات المرض هذه بين البيانات "السلبية". يتم ملاحظة هذا التناقض الداخلي هنا: (Yang et al. ، 2012) . انحرف الباحثون عن النهج التقليدي واعتبروا الجينات التي لا علاقة لها بجينات المرض المكتشفة بالفعل كخليط غير مسمى ، ثم طبقوا طرق التعلم PU.
مثال آخر هو التعلم المعزز القائم على عروض الخبراء. التحدي هو تدريب الوكيل على التصرف بنفس طريقة الخبير. يمكن تحقيق ذلك باستخدام طريقة التعلم المحاكي التوليدي (GAIL). يستخدم GAIL بنية شبيهة بـ GAN (شبكات الخصومة التوليدية): يولد الوكيل مسارات بحيث لا يستطيع التمييز (المصنف) تمييزها عن عروض الخبير. لاحظ باحثون من DeepMind مؤخرًا أنه في GAIL ، يحل المُميز مشكلة تعلم PU (Xu & Denil ، 2019)... عادة ، يعتبر المُميِّز بيانات الخبير إيجابية ، والبيانات الناتجة سلبية. هذا التقريب دقيق بما يكفي في بداية التدريب عندما يكون المولد غير قادر على إنتاج بيانات تبدو إيجابية. ومع ذلك ، مع تقدم التدريب ، تبدو البيانات التي تم إنشاؤها أشبه ببيانات الخبراء حتى يصبح من الصعب تمييزها عن أداة التمييز في نهاية التدريب. لهذا السبب ، يعتبر الباحثون (Xu & Denil ، 2019) أن البيانات التي تم إنشاؤها هي بيانات غير مسماة بنسبة مزيج متغيرة. في وقت لاحق ، تم تعديل GAN بطريقة مماثلة عند إنشاء الصور (Guo et al. ، 2020) .

الشكل: 3. تعلم PU كنظير لتصنيف PN القياسي
في الفئة الثانية ، يمكن استخدام تعلم PU لاكتشاف الشذوذ كتناظرية لتصنيف فئة واحدة (OCC). لقد رأينا بالفعل في المقدمة كيف يمكن أن تساعد البيانات غير المميزة بالضبط. جميع طرق OSS ، بدون استثناء ، مجبرة على افتراض توزيع البيانات السلبية. على سبيل المثال ، من الحكمة وضع دائرة حول البيانات الإيجابية في شكل بيضاوي (كرة زائدة في الحالة متعددة الأبعاد) ، تكون جميع النقاط خارجها سالبة. في هذه الحالة ، نفترض أن البيانات السلبية موزعة بالتساوي (بلانشارد وآخرون ، 2010)... بدلاً من وضع مثل هذه الافتراضات ، يمكن لأساليب تعلم PU تقدير توزيع البيانات السلبية بناءً على البيانات غير المسماة. هذا مهم بشكل خاص إذا كانت توزيعات الفئتين متداخلة بشدة (Scott & Blanchard ، 2009) . أحد الأمثلة على اكتشاف الشذوذ باستخدام التعلم PU هو اكتشاف المراجعة المزيفة (Ren et al. ، 2014) .

الشكل: 4. مثال على مراجعة وهمية
كشف الفساد في مزادات المشتريات العامة الروسية
يمكن أن تُعزى الفئة الثالثة من تعلم PU إلى المشكلات التي لا يمكن فيها استخدام تصنيف ثنائي أو فئة واحدة. على سبيل المثال ، سوف أخبركم عن مشروعنا لاكتشاف الفساد في مزادات المشتريات العامة الروسية (Ivanov & Nesterov ، 2019) .
وفقًا للتشريع ، فإن البيانات الكاملة عن جميع مزادات المشتريات العامة متاحة للجمهور لكل من يريد قضاء شهر في تحليلها. لقد جمعنا البيانات من أكثر من مليون مزاد أقيم في الفترة من 2014 إلى 2018. من وضع ، ومتى ، وكم ، ومن ربح ، وفي أي فترة تم المزاد ، ومن احتفظ ، وما اشترى - كل هذا موجود في البيانات. لكن ، بالطبع ، لا توجد تسمية "الفساد هنا" ، لذا لا يمكنك بناء مصنف عادي. بدلاً من ذلك ، قمنا بتطبيق تعلم PU. الافتراض الأساسي: المشاركون الذين يتمتعون بميزة غير عادلة سيفوزون دائمًا. باستخدام هذا الافتراض ، يمكن اعتبار الخاسرين في المزادات عادلين (إيجابيين) ، والفائزين محتمل أن يكونوا غير أمناء (بدون علامات).عند الإعداد بهذه الطريقة ، يمكن لأساليب تعلم PU أن تجد أنماطًا مشبوهة في البيانات بناءً على الفروق الدقيقة بين الفائزين والخاسرين. بالطبع ، من الناحية العملية ، تظهر الصعوبات: يلزم تصميم دقيق لميزات المصنف ، وتحليل قابلية تفسير تنبؤاته ، والتحقق الإحصائي من الافتراضات حول البيانات.
وفقًا لتقديراتنا المتحفظة للغاية ، فإن حوالي 9 ٪ من المزادات في البيانات فاسدة ، ونتيجة لذلك تخسر الدولة حوالي 120 مليون روبل سنويًا. قد لا تبدو الخسائر كبيرة جدًا ، لكن المزادات التي ندرسها لا تشغل سوى حوالي 1٪ من سوق المشتريات العامة.


الشكل: 5. حصة مزادات المشتريات العامة الفاسدة في مناطق مختلفة من روسيا (Ivanov & Nesterov ، 2019)
الملاحظات الختامية
من أجل عدم خلق انطباع بأن PU هو الحل لجميع مشاكل الإنسانية ، سأذكر المزالق. في التصنيف التقليدي ، كلما زادت البيانات التي لدينا ، يمكن أن يكون المصنف أكثر دقة. علاوة على ذلك ، بزيادة كمية البيانات إلى ما لا نهاية ، يمكننا الاقتراب من المصنف المثالي (وفقًا لصيغة بايزي). لذا ، فإن المصيد الرئيسي لتعلم PU هو أنها مشكلة غير موضوعية ، أي مشكلة لا يمكن حلها بشكل لا لبس فيه حتى مع وجود كمية غير محدودة من البيانات. يصبح الوضع أفضل إذا كانت نسبة فئتين في البيانات غير المصنفة معروفة ، ومع ذلك ، فإن تحديد هذه النسبة يعد أيضًا مشكلة غير موضوعية (Jain et al. ، 2016)... أفضل ما يمكننا تحديده هو التباعد بين النسبة. علاوة على ذلك ، غالبًا لا تقدم طرق التعلم PU طرقًا لتقدير هذه النسبة واعتبارها معروفة. هناك طرق منفصلة لتقديرها (تسمى المهمة تقدير نسبة الخليط) ، لكنها غالبًا ما تكون بطيئة و / أو غير مستقرة ، خاصةً عندما يتم تمثيل الفئتين بشكل غير متساوٍ في الخليط.
في هذا المنشور ، تحدثت عن التعريف والتطبيق البديهي لتعلم PU. بالإضافة إلى ذلك ، يمكنني أن أخبرك عن التعريف الرسمي لتعلم PU مع الصيغ وتفسيراتها ، وكذلك عن طرق تعلم PU الكلاسيكية والحديثة. إذا أثار هذا المنشور الاهتمام ، سأكتب تكملة.
فهرس
Blanchard, G., Lee, G., & Scott, C. (2010). Semi-supervised novelty detection. Journal of Machine Learning Research, 11(Nov), 2973–3009.
Elkan, C., & Noto, K. (2008). Learning classifiers from only positive and unlabeled data. Proceeding of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining — KDD 08, 213. https://doi.org/10.1145/1401890.1401920
Guo, T., Xu, C., Huang, J., Wang, Y., Shi, B., Xu, C., & Tao, D. (2020). On Positive-Unlabeled Classification in GAN. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8385–8393.
Ivanov, D. I., & Nesterov, A. S. (2019). Identifying Bid Leakage In Procurement Auctions: Machine Learning Approach. ArXiv Preprint ArXiv:1903.00261.
Jain, S., White, M., Trosset, M. W., & Radivojac, P. (2016). Nonparametric semi-supervised learning of class proportions. ArXiv Preprint ArXiv:1601.01944.
Kiryo, R., Niu, G., du Plessis, M. C., & Sugiyama, M. (2017). Positive-unlabeled learning with non-negative risk estimator. Advances in Neural Information Processing Systems, 1675–1685.
Ren, Y., Ji, D., & Zhang, H. (2014). Positive Unlabeled Learning for Deceptive Reviews Detection. EMNLP, 488–498.
Scott, C., & Blanchard, G. (2009). Novelty detection: Unlabeled data definitely help. Artificial Intelligence and Statistics, 464–471.
Xu, D., & Denil, M. (2019). Positive-Unlabeled Reward Learning. ArXiv:1911.00459 [Cs, Stat]. http://arxiv.org/abs/1911.00459
Yang, P., Li, X.-L., Mei, J.-P., Kwoh, C.-K., & Ng, S.-K. (2012). Positive-unlabeled learning for disease gene identification. Bioinformatics, 28(20), 2640–2647.