رياضيات المسافة الاجتماعية هي درس في الهندسة

يكمن التحدي المتمثل في كيفية إعادة فتح المكاتب والمدارس والأماكن العامة الأخرى بأمان مع إبقاء الناس على مسافة متر ونصف إلى سؤال يدرسه علماء الرياضيات منذ قرون.

قد يبدو أن موضوعًا مثل تعبئة المجالات سوف يروق فقط لعلماء الرياضيات. من هو الآخر الذي قد يكون مهتمًا بالبحث عن أكثر الطرق فعالية لوضع الدوائر على مستوٍ أو كرات في الفضاء؟



ومع ذلك ، اليوم الملايين من الناس حول العالم يفكرون بالضبط هذه المهمة.



يعد تحديد كيفية فتح المباني والأماكن العامة بأمان مع الحفاظ على مسافة اجتماعية ، على وجه الخصوص ، تمرينًا في الهندسة. إذا كان يجب أن يكون كل شخص على بعد متر ونصف على الأقل من الأشخاص الآخرين ، فعندئذٍ لحساب عدد الأشخاص الذين يمكنهم الجلوس في الفصل أو غرفة الطعام ، تحتاج إلى حزم دوائر غير متداخلة في مخطط الأرضية.







بطبيعة الحال ، لمكافحة الفيروس التاجي ، هناك العديد من المشاكل التي يجب حلها أكثر من هذه المشكلة الهندسية. ومع ذلك ، فإن تعبئة الدوائر والمجالات يلعب دورًا في هذا - تمامًا مثل نمذجة الهياكل البلورية في الكيمياء ومساحات الرسائل المجردة في نظرية المعلومات. هذه المهمة ، التي تبدو بسيطة في الوصف ، شغلت أذهان أعظم علماء الرياضيات في التاريخ ، ويتم إجراء أكثر الأبحاث إثارة للاهتمام في هذا المجال اليوم ، على وجه الخصوص ، في أبعاد أعلى. على سبيل المثال ، وجد علماء الرياضيات مؤخرًا أفضل طريقة للتعبئة في مسافات 8 و 24 بعدًا - وهي تقنية مطلوبة لتحسين رموز تصحيح الأخطاء المستخدمة في الهواتف المحمولة وفي التواصل مع المسابير الفضائية. لذلك دعونا نلقي نظرة على بعض التعقيدات غير المتوقعة التي تنشأ عندما نحاول ملء فراغ بأبسط صورة.



سواء كنت تقوم بتعبئة البرتقال في صناديق في العمل أو جلوس الطلاب بأمان مع تباعد اجتماعي ، فإن حجم وشكل الحاوية الخاصة بك أمر بالغ الأهمية لمهمتك. ومع ذلك ، بالنسبة لمعظم علماء الرياضيات ، فإن نظرية تعبئة المجال تدور حول ملء الفراغ بأكمله. في بعدين ، هذا يعني تغطية المستوى بدوائر منفصلة من نفس الحجم.



فيما يلي مثال على دوائر التعبئة على متن طائرة. يبدو وكأنه منظر علوي لحزمة الصودا:







يمكنك أن تتخيل كيف يتكرر هذا النمط في جميع الاتجاهات ، مثل البلاط الذي تم رصفه بمستوى. تشير الفجوات الصغيرة بين الدوائر إلى أن المستوى غير ممتلئ تمامًا ، ولكن في حالة دوائر التعبئة ، يجب توقع ذلك. نحن مهتمون بنسبة تغطية الطائرة. سيكون هذا هو "كثافة التعبئة" لطريقة معينة.



الطريقة المذكورة أعلاه تسمى التعبئة المربعة ، ولسبب وجيه - يمكن تمثيل مراكز الدوائر كرؤوس المربعات.







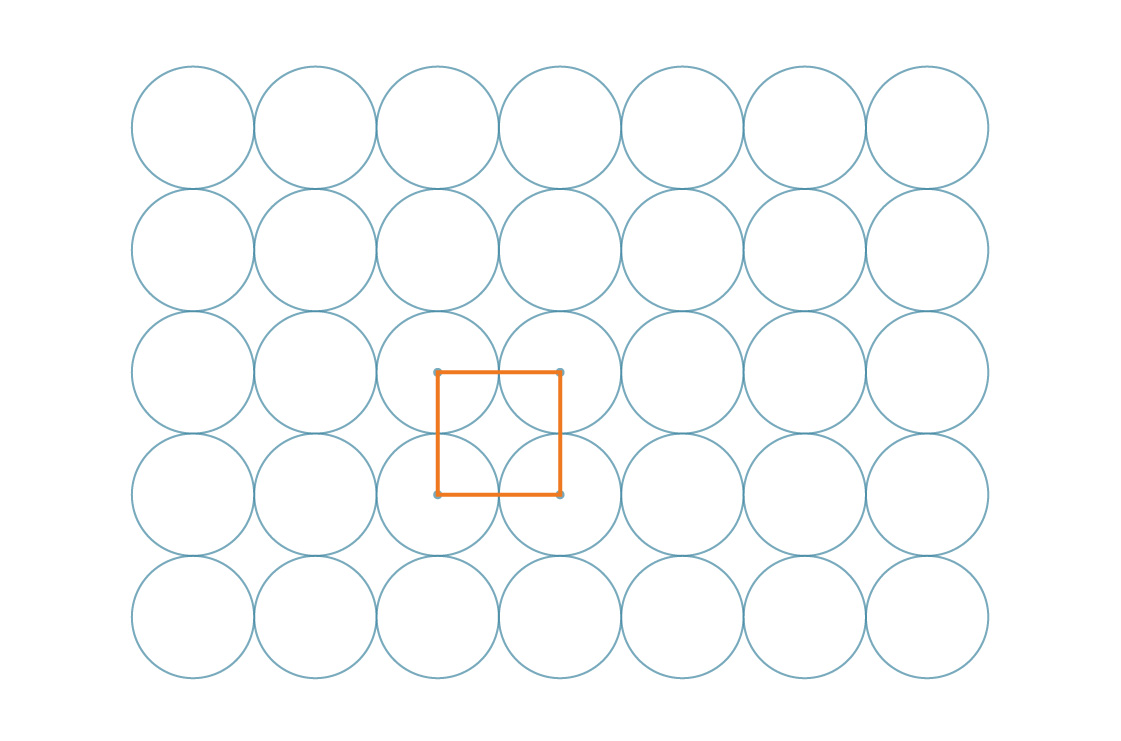
وفي الواقع ، هذه المربعات نفسها قامت بتقسيم المستوي:







يتم تسهيل مهمتنا من خلال تماثل النمط. نظرًا لأن هذه المربعات تغطي المستوى بأكمله بطريقة دورية ، فإن النسبة المئوية للمستوى التي تغطيها الدوائر هي نفس النسبة المئوية للمربع الذي تغطيه الدوائر. لنلقِ نظرة على أحد هذه المربعات.







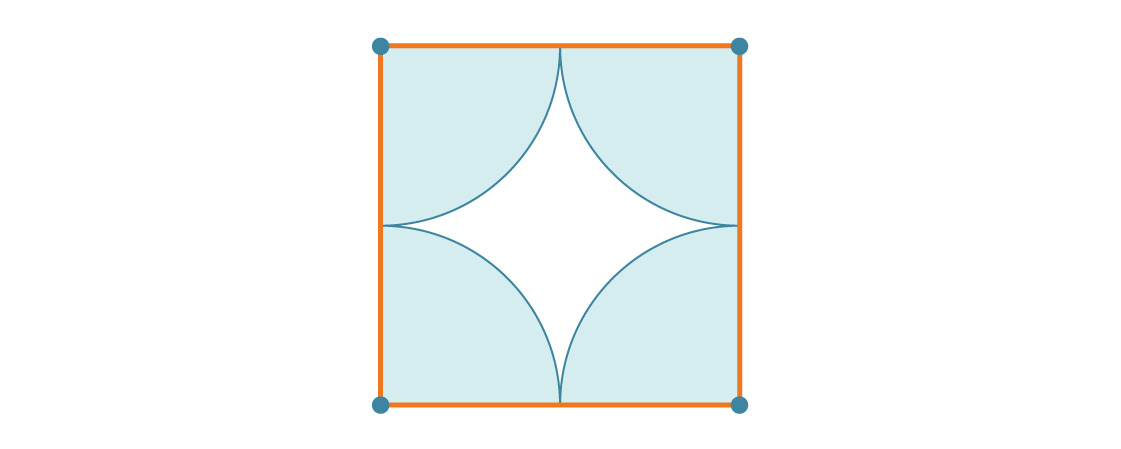
لنفترض أن نصف قطر الدائرة هو r. هذا يعني أن طول ضلع المربع يساوي 2r. يوجد في كل رأس من رؤوس المربع ربع دائرة ، وبالتالي فإن النسبة المئوية لتغطية كل مربع تساوي ببساطة نسبة مساحة دائرة كاملة إلى مساحة مربع واحد كامل:

$$

$$\frac{\pi r^2}{(2r)^2} = \frac{\pi r^2}{4r^2} = \frac{\pi }{4} \approx 0,7854$$

كل مربع مغطى بدوائر بنسبة 78.54٪ ، لذا فبالنظر إلى تبليط المستوى ، فإن مجمله يغطي حوالي 78.54٪ بدوائر هذه هي كثافة التعبئة المربعة. لاحظ أن نصف القطر r اختفى من الإجابة. وهذا منطقي: بغض النظر عن حجم الدوائر ، سيظل هناك أربعة أرباع دائرة في المربع.



إذا حاولت طي علب الصودا على الجانب مثل هذا ، وانزلقت وملء الفراغات ، فأنت تعلم أن هناك طريقة أخرى لتعبئة الدوائر على متن الطائرة:







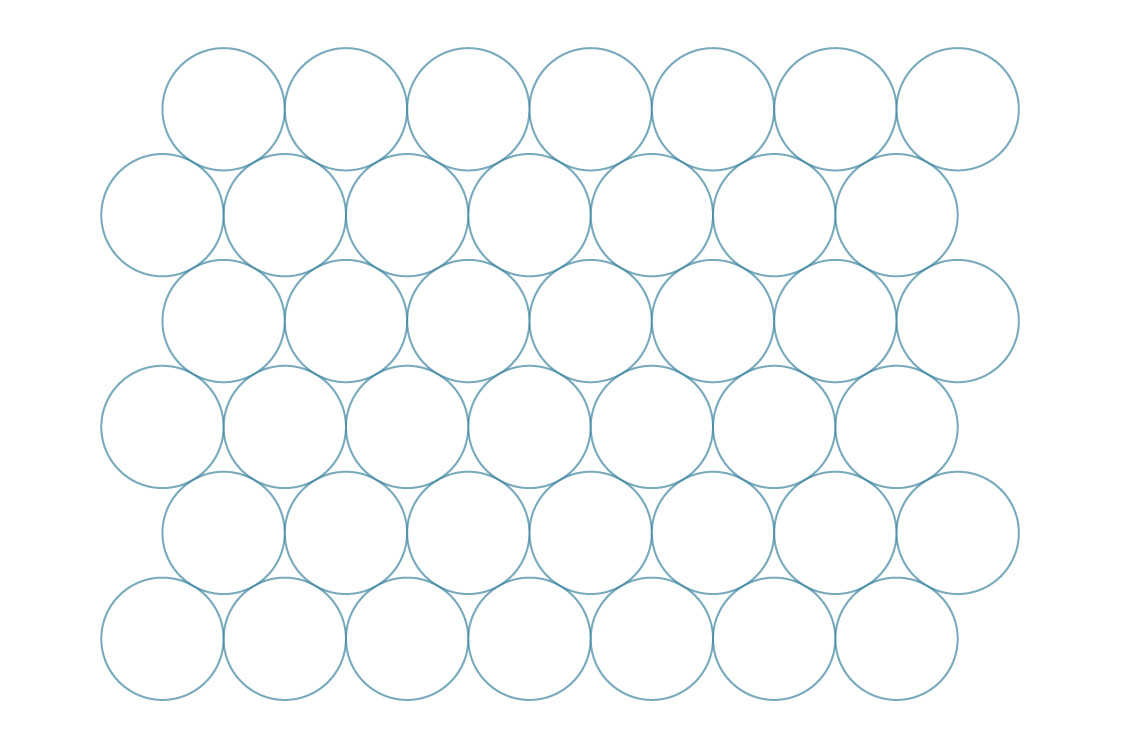
دعنا نتبع نهجًا مشابهًا للطريقة السابقة وتخيل أن مراكز الدوائر في هذه الحالة تشكل سداسيات منتظمة ...







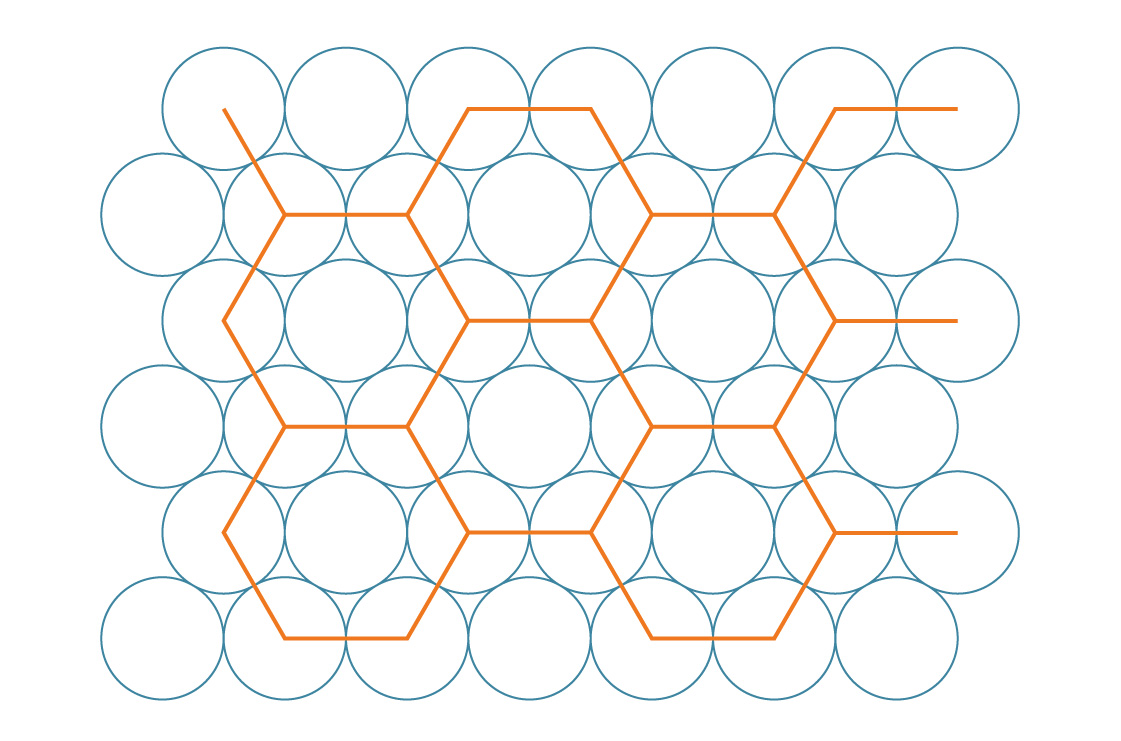
نسمي هذا التعبئة السداسية. يبدو أن هذه الطريقة تملأ الفجوات بشكل أكثر كفاءة من التربيع. للتحقق من ذلك ، دعنا نقارن كثافات التعبئة. السداسيات ، مثل المربعات ، تقطع المستوى بالكامل ، لذا يمكننا تحديد كثافة هذه الطريقة من خلال تحليل سداسي واحد.







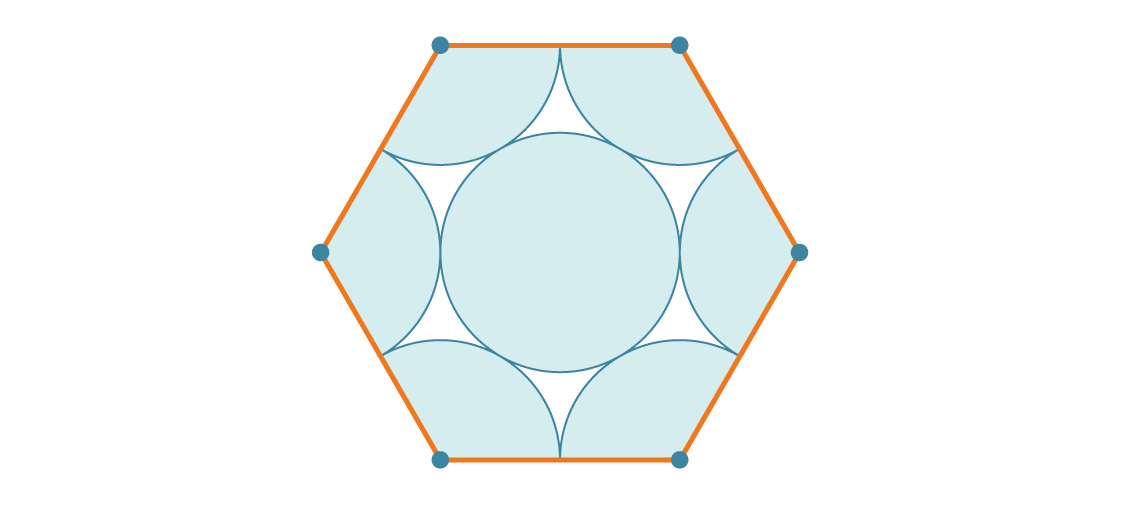
أي جزء من الشكل السداسي مغطى بالدوائر؟ نظرًا لأن الشكل السداسي العادي له زاوية داخلية مقدارها 120 درجة ، فإن هناك ثلث دائرة في كل ركن من أركانه. تظهر دائرتان كاملتان ، والدائرة الوسطى هي الثالثة. إذن ، كل سداسي مغطى بثلاث دوائر. إذا كان نصف قطر كل دائرة هو r ، فإن المساحة تساوي 3πr².







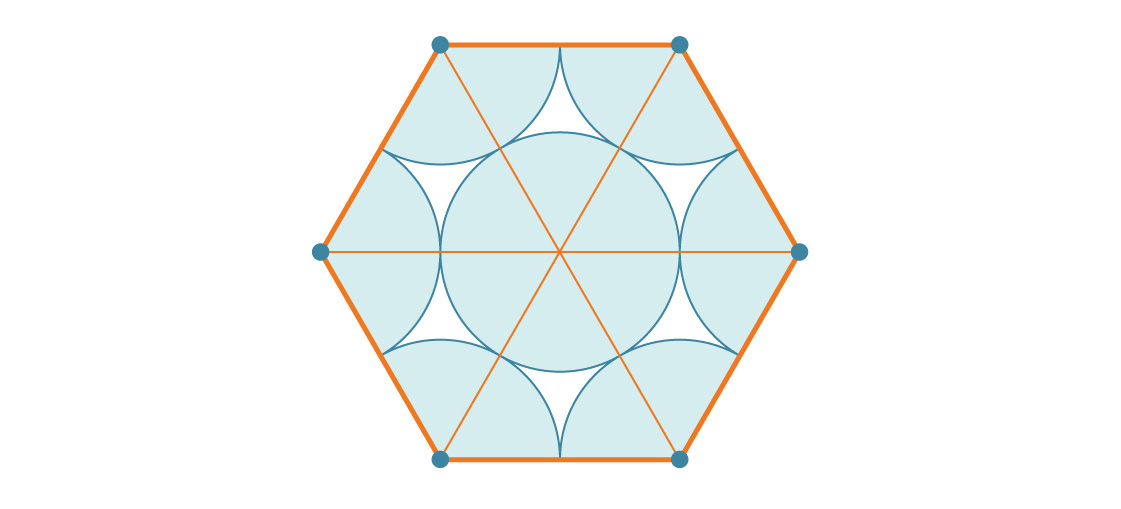
كيف يقارن هذا بمساحة الشكل السداسي؟ سداسي الأضلاع بطول ضلعه s يساوي ستة مثلثات متساوية الأضلاع بطول ضلعها s ، كل منها s ² √3 / 4. إذن ، مساحة الشكل السداسي هي 6 * s ² 3/4 = 6 s ² √3 / 4. نظرًا لأن طول ضلع السداسي هو 2r ، فإن مساحته هي:

$$

$$\frac{6 s^2 \sqrt3}{4} = \frac{6 (2r)^2 \sqrt3}{4} = \frac{24 r^2 \sqrt3}{4} = 6 r^2 \sqrt3$$

يمكنك الآن حساب النسبة المئوية للمسدس الذي تغطيه الدوائر (بقسمة مساحة الدوائر الست على مساحة الشكل السداسي):

$$

$$\frac{3 \pi r^2}{6 r^2 \sqrt3} = \frac{3 \pi}{6 \sqrt3} = \frac{\pi}{2 \sqrt3} \approx 0,9069$$

كل سداسي مغطى بنسبة 90.69٪ بدوائر ، لذلك ستكون هذه العبوة أكثر كفاءة من المربع. لاحظ كيف يختفي نصف قطر الدائرة مرة أخرى كما هو متوقع. في الواقع ، لا يوجد تغليف أكثر كفاءة.



لكن لم يكن من السهل إثبات ذلك. علماء الرياضيات الشهير مثل جوزيف لويس لاغرانج و كارل فريدريش غاوس بدأت العمل على هذا في أواخر 18 وأوائل القرن 19، ولكن تم حل المشكلة تماما إلا في 1940s، من خلال تجهيز بعناية كل الترتيبات الممكنة - دورية وغير دورية. إن حقيقة أن الأمر استغرق الكثير من الوقت لحل المشكلة في بعدين ، حيث يسهل تخيل كل شيء ، قد يكون بمثابة تحذير لما ينتظرنا في الأبعاد الأعلى.



تعد مجالات التعبئة في ثلاثة أبعاد مهمة أكثر صعوبة ، على الرغم من أنها تحمل بعض أوجه التشابه مع ابن عمها ثنائي الأبعاد. على سبيل المثال ، تتكون العبوات ثنائية الأبعاد التي نظرنا فيها من طبقة واحدة.







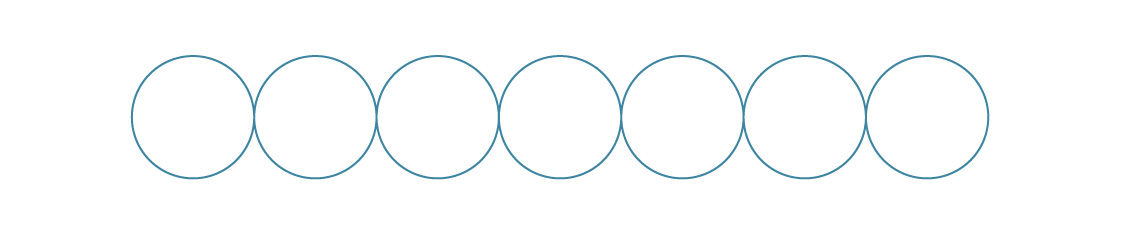
بالنسبة للحزمة المربعة ، نضع كل طبقة فوق الطبقة السابقة.







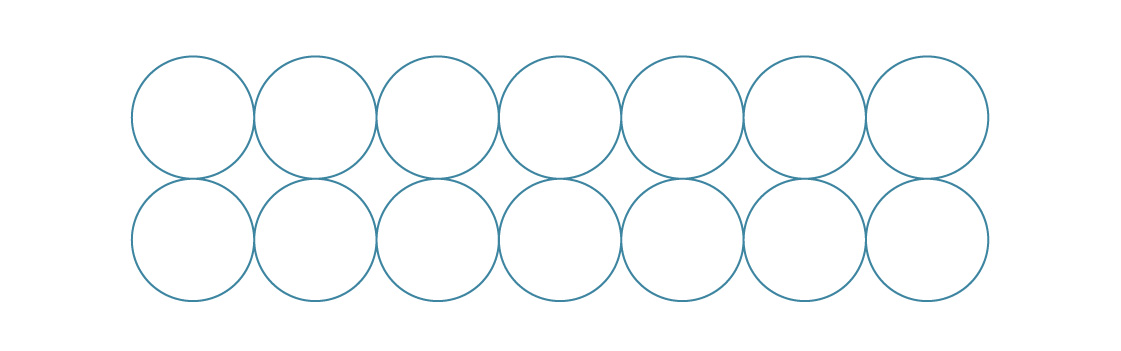
بالنسبة للتعبئة السداسية ، قمنا بوضع طبقات جديدة بين الطبقات السابقة.







يتم الحصول على عبوات مختلفة اعتمادًا على كيفية دمج نسخ الطبقات المختلفة.



في ثلاثة أبعاد ، يخلق هذا الترتيب للطبقات فوق بعضها البعض عبوات مختلفة بشكل أساسي.







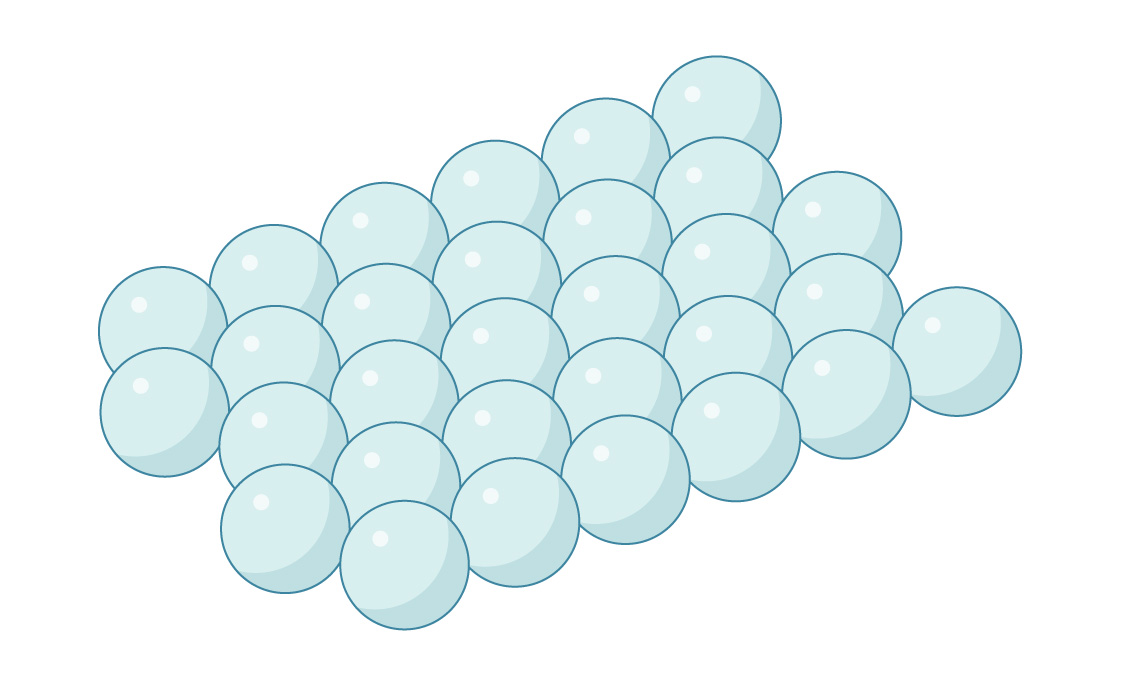
هذه طبقة من الكرات معبأة بشكل سداسي ، كما توحي التعبئة المثالية للدوائر على المستوى. وبالمثل ، يمكنك وضع الطبقة الثانية أعلى الطبقة الأولى عن طريق وضع المجالات في المسافات بين المجالات السفلية.







لكن في الأبعاد الثلاثة ، تصبح الهندسة أكثر تعقيدًا بعض الشيء. في كل طبقة من المجالات ، تبين أن المسافة بين الفجوات المتجاورة أقل من المسافة بين مراكز الكرات. لذلك ، لا يمكنك لصق كرة في كل فجوة - سوف تتقاطع. لذلك ، تصطف الفجوات في الطبقتين لإنشاء قنوات تمر عبر الحزمة.







هناك طريقتان لوضع الطبقة الثالثة. يمكنك محاذاة الفجوات مع الفجوات السفلية ، وترك القنوات مفتوحة. فيما يلي عرض جانبي لهذا الترتيب:







للحفاظ على القنوات مفتوحة ، تحتاج إلى وضع الكرات في الطبقة الثالثة فوق الكرات من الطبقة الأولى مباشرةً. يسمى هذا الترتيب من الكرات "حشوة سداسية كثيفة" (صومعة) ، وإذا نظرت إليها من الأعلى ، يمكنك رؤية فجوات مفتوحة تمر من خلالها.







خيار آخر لوضع الطبقة الثالثة هو إغلاق القنوات. يتم وضع الكرات الموجودة في الطبقة الثالثة مباشرة فوق فجوات الطبقة الأولى:







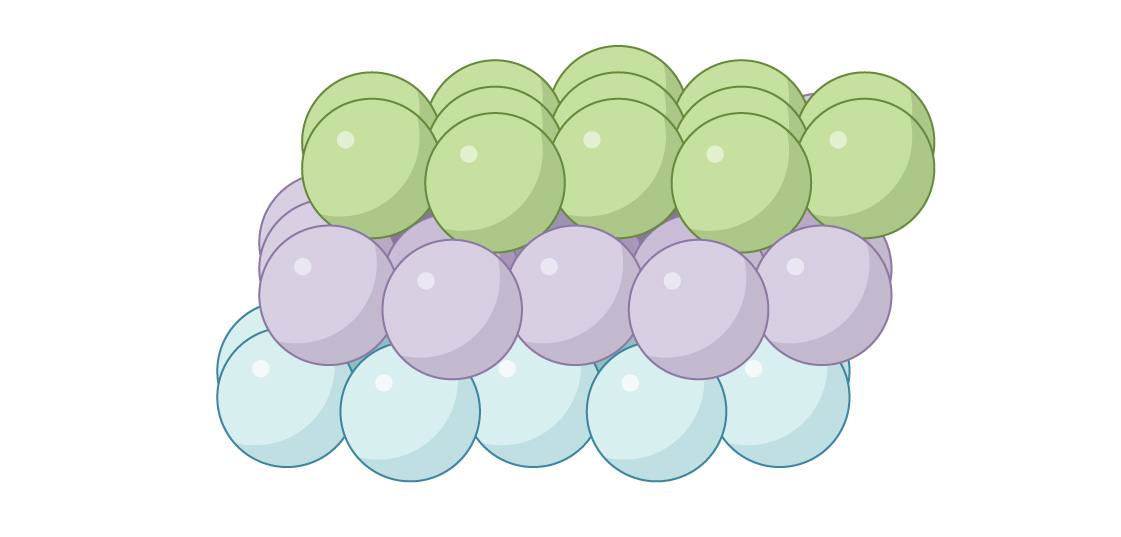
وهذا ما يسمى "مكعب متمركز على الوجه" (FCC) أو "تعبئة مكعبة قريبة". عندما ينظر إليها من أعلى ، لن تكون هناك فجوات.







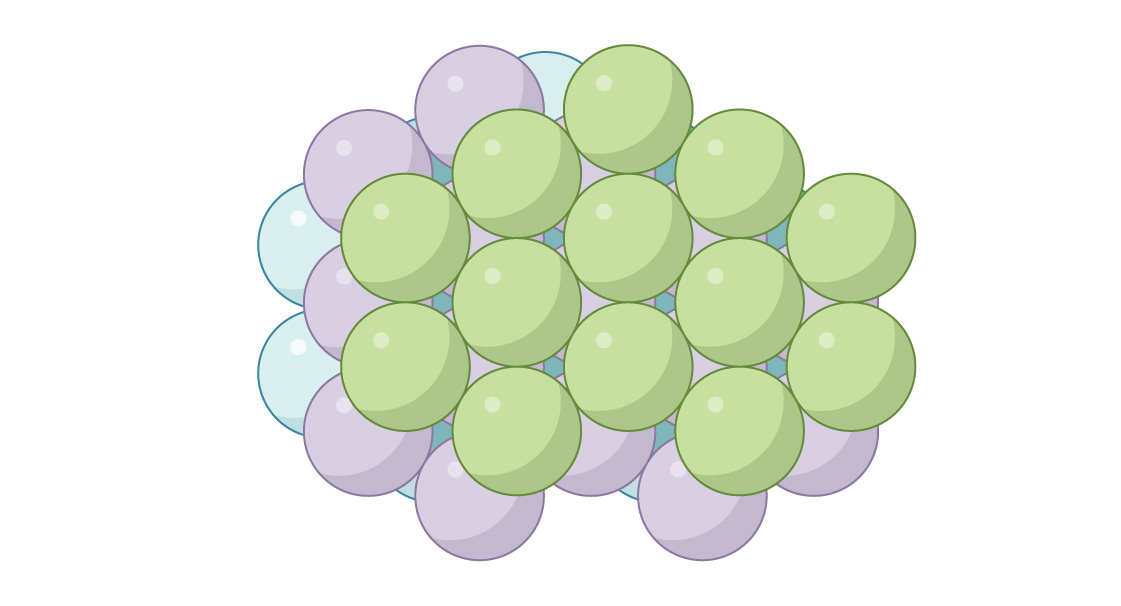
ينشأ هذان الترتيبان المتشابهان ولكن المختلفان جوهريًا في الكيمياء ، ويصفان ترتيب الذرات في مواد مختلفة. على سبيل المثال ، في المعادن مثل الفضة والذهب ، يكون للهيكل شكل HA ، وفي المعادن مثل الزنك والتيتانيوم - الصوامع. تسمح لك كل من الطريقتين بملء الفراغ بالكرات. في طريقة الصومعة ، في كل طبقة ثانية توجد الكرات متماثلة تمامًا ، وفي GK - في كل ثلث. يمكنك إنشاء عدد لا حصر له من الحزم المختلفة من خلال الجمع بين كلتا الطريقتين ، ولكن من المثير للاهتمام أن كلا من الصومعة و GK يوفران تغليفًا مثاليًا! كثافة التعبئة ليست هي نفسها فقط ، π 3√2 0.7405 هي أكثر تعبئة ممكنة في الفضاء ثلاثي الأبعاد. اقترح عالم الرياضيات والفلك الشهير يوهانس كيبلر ذلك في عام 1611 ، لكنه دليل كاملفقط عالم الرياضيات توماس هالز كان قادرًا على الاستدلال في عام 1998.







هناك مساحة أكبر في الفضاء ثلاثي الأبعاد ، ولدينا المزيد من الطرق لتعبئة الكرات بشكل فعال. عندما تضيف أبعادًا ، يزداد تعقيد العبوة فقط - هناك مساحة أكبر وخيارات أكثر ويصعب تخيلها. بالإضافة إلى ذلك ، تصبح الكرات أصغر في الأبعاد الأعلى!







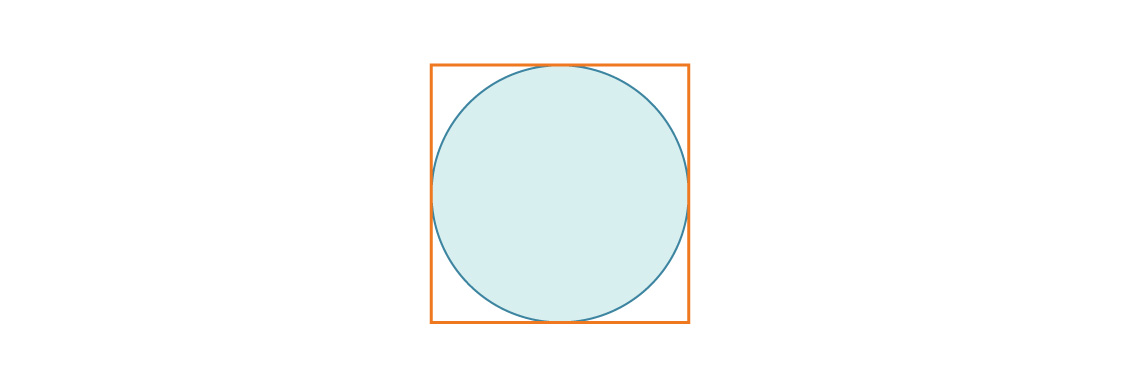
لنتأمل دائرة منقوشة في مربع بطول ضلع 1.



نصف قطر الدائرة هو r = 1/2 ، وبالتالي فإن نسبة مساحة الدائرة إلى مساحة المربع هي:

$$

$$\frac{\pi r^2}{s^2} = \frac{\pi (\frac{1}{2})^2}{1^2} = \frac{\pi }{4} \approx 0,7854$$

وهو ما يساوي أيضًا كثافة تعبئة المربع في بعدين.



لننظر الآن إلى حجم الكرة المدرجة في مكعب وحدة.







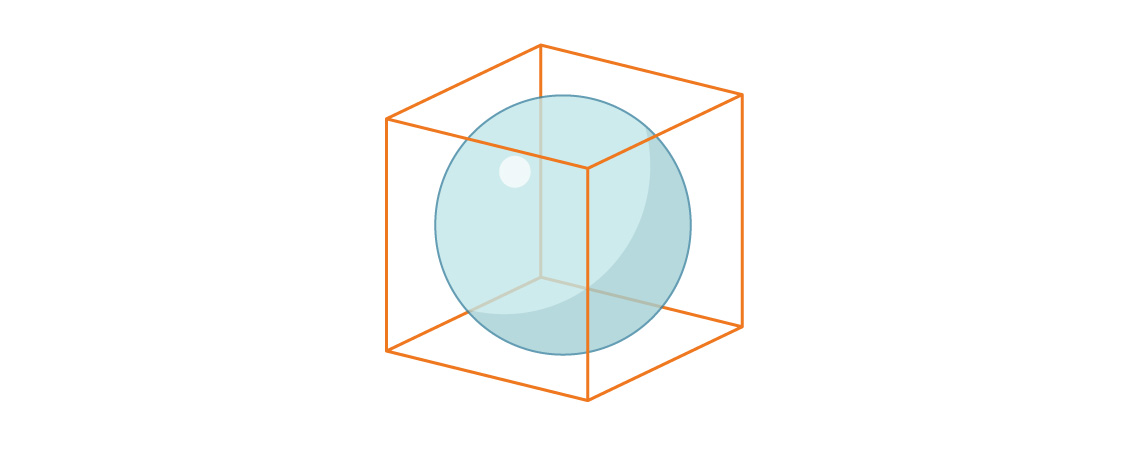
يساوي نصف قطر الكرة مرة أخرى r = 1/2 ، وبالتالي فإن نسبة حجم الكرة إلى حجم المكعب هي:

$$

$$\frac{\frac{4}{3}\pi r^3}{s^3} = \frac{\frac{4}{3}\pi (\frac{1}{2})^3}{1^3} = \frac{4}{3}\pi (\frac{1}{8}) = \frac{\pi}{6} \approx 0,5236$$

لاحظ أن جزء المكعب الذي تشغله كرة منقوشة بثلاثة أبعاد أقل من جزء المربع الذي تشغله دائرة منقوشة في بعدين. يستمر هذا النمط: مع زيادة الأبعاد ، تقل هذه النسبة. مع نمو n ، تحتل المجالات ذات الأبعاد n مساحة أقل وأقل من n.



يمكن إظهار ذلك باستخدام الجبر ، ولكن يمكن أيضًا فهمه إذا فكرت في الزوايا. في أي بُعد ، يمكن نقش كرة ذات بُعد n في مكعب ذي بُعد n. الكرة تلامس حواف المكعب ولكنها لا تصل إلى الزوايا ، لذلك توجد منطقة حول كل زاوية داخل المكعب ولكن خارج الكرة. ومع ذلك ، سيكون للصندوق ذي الأبعاد ⁿ 2 ⁿالزوايا ، أي بزيادة في n ، يزداد عدد المناطق التي لا تغطيها الكرة أضعافًا مضاعفة. بالإضافة إلى ذلك ، تزداد المسافة بين الزوايا والكرة أيضًا. هذا يعني أنه على المدى الطويل ، فإن المساحة الموجودة داخل المكعب ذي البعد n ، ولكن خارج الكرة ذات البعد n ، ستسحق ببساطة المساحة التي تشغلها الكرة.



إذا بدا انكماش الكرات غريبًا بما يكفي بالنسبة لك ، فإن علماء الرياضيات المشاركين في تعبئة الكرات لاحظوا شيئًا غير متوقع أكثر في الأبعاد 8 و 24. في هذه الأبعاد ، تتقلص الكرات بما يكفي لتتمكن من ملء الفجوات بين الكرات الجديدة ، مما يعطي تغليفًا شديد الكثافة في هذه الأبعاد ... تم طرح فرضية حول أمثلية هذه الأساليب الخاصة ، لكنها لم تكن معروفة بالضبط حتى عام 2016 ، عندما أثبتت مارينا فيازوفسكايا هذه النظريةلمساحة 8 أبعاد. بعد أسبوع ، وسعت فيازوفسكايا ومساعدوها طريقتها لإثبات الحالة في مساحة 24 بعدًا.



يترتب على عمل Vyazovskaya أننا نعرف الآن أكثر الطرق فعالية لتعبئة الكرات في الأبعاد 1 و 2 و 3 و 8 و 24. ولكن في الأبعاد الأخرى ، لا يزال هناك الكثير من العمل الذي يتعين القيام به. لذا أخرج عبوات البرتقال والصودا وابدأ التجربة. قد تكون الشخص الذي يمكنه سد الثغرات المهمة.

تمارين

1. لنفترض أننا بدأنا في تعبئة المستوى الإحداثي كما هو موضح في الصور أدناه. يقع مركز الدائرة اليسرى السفلية عند النقطة (0 ، 0) ، ويقع مركز الدائرة اليمنى السفلية عند النقطة (2 ، 0).







أين مركز الدائرة الثالثة؟



2. يوجد أدناه بداية التعبئة "المكعبة البسيطة" للكرات. ما هي كثافة التعبئة لهذا المخطط؟







3. هنا بداية تعبئة الطائرة في مثمن منتظم.







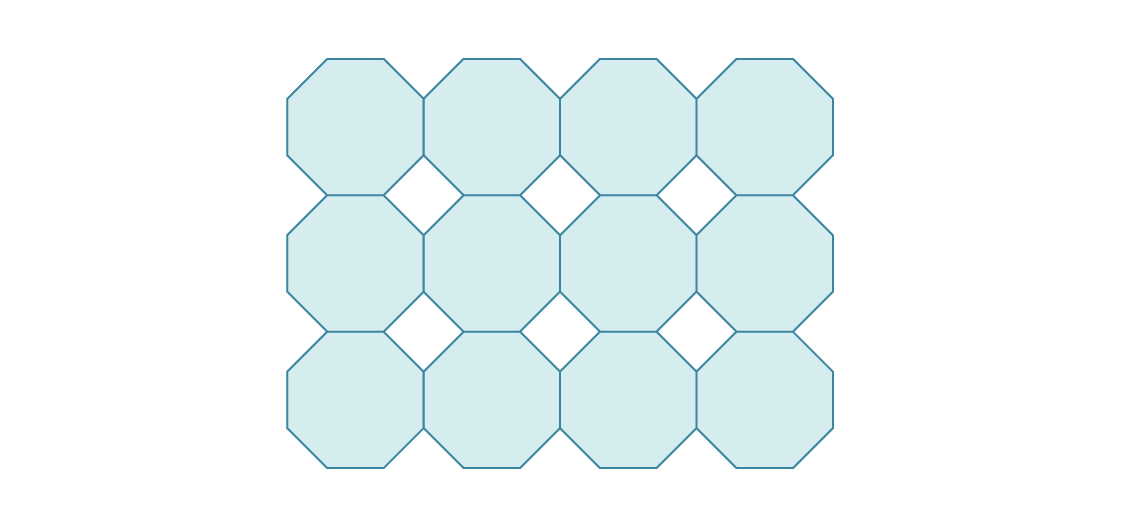
ما هي كثافة هذه العبوة؟

الإجابات

أنظر أيضا:

• " جوجل تطلق Sodar ، أداة AR لعرض المسافة الاجتماعية "
• " Meta-study تكشف عن فعالية الأقنعة والتباعد عن SARS-CoV-2 (COVID-19) "
• " كوفيد -19: نموذج التنبؤ البارامترى الوبائي "