هذه بداية قصة حول كيفية غزو الرياضيات للجيولوجيا لأول مرة ، وكيف أتى متخصص في تكنولوجيا المعلومات وبرمج كل شيء ، وبالتالي خلق مهنة جديدة لـ "الجيولوجي الرقمي". هذه قصة حول كيفية اختلاف النمذجة العشوائية عن كريجينج. إنها أيضًا محاولة لإظهار كيف يمكنك كتابة أول برنامج جيولوجي بنفسك ، وربما ، بطريقة ما ، تحويل مجال الهندسة الجيولوجية والبترولية.
دعنا نحسب كمية الزيت الموجودة
, , , , . , , . , (, ). , , , .
— , , , , , , , .
, — . , — . — . , ( , , ) . . , , ( , , ).
. , , , , . — , , . — , , , . , , .
. ; , , , .
, , . , , , , . , .
, , , . , , . , . . , , , - , .
, — , .
, , .. , , . , , , . — — «support». , , , , . .
, , (Krige, D.G. 1951. A statistical approach to some basic mine valuation problems on the Witwatersrand. Journal of the Chemical, Metallurgical and Mining Society of South Africa, December 1951. pp. 119–139.). , -, , , , . , , 5×5 , , , 1 , 50 ×50 ×1 — , , ( — upscaling).
. , — . .
. ,
.
— , . , . , , , .
:
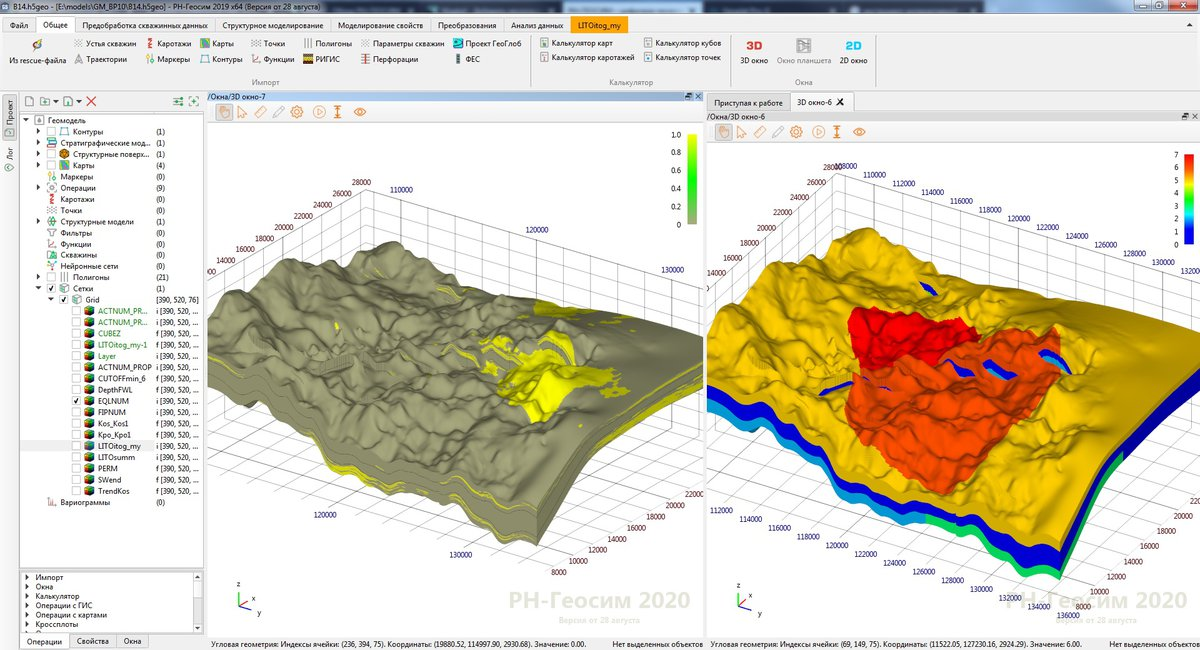
— . (. . 1). , . , . , . , , 1, , .
Python .
import numpy as np
import matplotlib.pyplot as pl
# num of data
N = 5
np.random.seed(0)
# source data
z = np.random.rand(N)
u = np.random.rand(N)
x = np.linspace(0, 1, 100)
y = np.zeros_like(x)
# norm weights
w = np.zeros_like(x)
# power
m = 2
# interpolation
for i in range(N):
y += z[i] * 1 / np.abs(u[i] - x) ** m
w += 1 / np.abs(u[i] - x) ** m
# normalization
y /= w
# add source data
x = np.concatenate((x, u))
y = np.concatenate((y, z))
order = x.argsort()
x = x[order]
y = y[order]
# draw graph
pl.figure()
pl.scatter(u, z)
pl.plot(x, y)
pl.show()
pl.close()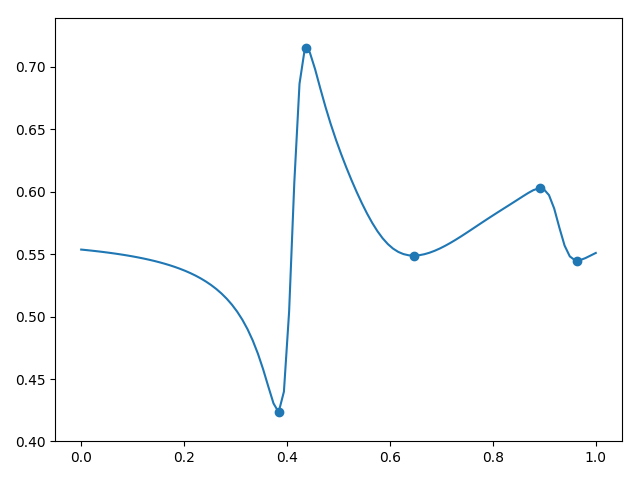
1.
. , , - . , , . -, , , , ? , . , 1 . , , . , , (. . 2). .

2.
, , , , . , , . , . — , , : , , , . , .
(2) :
, , . , , - - . .
, :
- , — . (4) — «», . . , (1):
. , — , — , — «» . , , (6),
(6) ( ). (4) , , dual kriging. (6) (3), , . , (7) , , , , ( ).
(. . 3). , , .
, — Python:
import numpy as np
import matplotlib.pyplot as pl
# num of data
N = 5
np.random.seed(0)
# source data
z = np.random.rand(N) - 0.5
u = np.random.rand(N)
x = np.linspace(0, 1, 100)
y = np.zeros_like(x)
# covariance function
def c(h):
return np.exp(-np.abs(h ** 2 * 20.))
# covariance matrix
C = np.zeros((N, N))
for i in range(N):
C[i, :] = c(u - u[i])
# dual kriging weights
lamda = np.linalg.solve(C, z)
# interpolation
for i in range(N):
y += lamda[i] * c(u[i] - x)
# add source data
x = np.concatenate((x, u))
y = np.concatenate((y, z))
order = x.argsort()
x = x[order]
y = y[order]
# draw graph
pl.figure()
pl.scatter(u, z)
pl.plot(x, y)
pl.show()
pl.close()
3.
, , . (5) (6) , .
, , . , , , .
. , (), , , , . , «», . , (6), , «», . , «» . : . , , , — . , , .
. , . . , , .
.
from theory import probability
from numpy import linalg, , .
, . () : u , ( ). , .
. . , ( , ).
, - — . - , . : — ( ), , , , . — , .
( , ) . — . , u , .
, , : . -, — «» (4), : . , , .., , , .
, , , , . , , . , , . .
, ( ). :
, , , , . . , , , ( ) , , . . .
, ( , , — , ). , (. . 4).
import numpy as np
import matplotlib.pyplot as pl
np.random.seed(0)
# source data
N = 100
x = np.linspace(0, 1, 100)
# covariance function
def c(h):
return np.exp(-np.abs(h ** 2 * 250))
# covariance matrix
C = np.zeros((N, N))
for i in range(N):
C[i, :] = c(x - x[i])
# eigen decomposition
w, v = np.linalg.eig(C)
A = v @ np.diag(w ** 0.5)
# you can check, that C == A @ A.T
# independent normal values
zeta = np.random.randn(N)
# dependent multinormal values
Z = A @ zeta
# draw graph
pl.figure()
pl.plot(x, Z)
pl.show()
pl.close()
4.
, , ( , ). , 5.
import numpy as np
import matplotlib.pyplot as pl
np.random.seed(3)
# source data
M = 5
# coordinates of source data
u = np.random.rand(M)
# source data
z = np.random.randn(M)
# Modeling mesh
N = 100
x = np.linspace(0, 1, N)
# covariance function
def c(h):
return np.exp(−np.abs(h ∗∗ 2 ∗ 250))
# covariance matrix mesh−mesh
Cyy = np.zeros ((N, N))
for i in range (N):
Cyy[ i , : ] = c(x − x[i])
# covariance matrix mesh−data
Cyz = np.zeros ((N, M))
# covariance matrix data−data
Czz = np.zeros ((M, M))
for j in range (M):
Cyz [:, j] = c(x − u[j])
Czz [:, j] = c(u − u[j])
# posterior covariance
Cpost = Cyy − Cyz @ np.linalg.inv(Czz) @ Cyz.T
# lets find the posterior mean, i.e. Kriging interpolation
lamda = np.linalg.solve (Czz, z)
y = np.zeros_like(x)
# interpolation
for i in range (M):
y += lamda[i] ∗ c(u[i] − x)
# eigen decomposition
w, v = np.linalg.eig(Cpost)
A = v @ np.diag (w ∗∗ 0.5)
# you can check, that Cpost == A@A.T
# draw graph
pl.figure()
for k in range (5):
# independent normal values
zeta = np.random.randn(N)
# dependent multinormal values
Z = A @ zeta
pl.plot(x, Z + y, color=[(5 − k) / 5] ∗ 3)
pl.plot(x, Z + y, color=[(5 − k) / 5] ∗ 3, label=’Stochastic realizations’)
pl.plot(x, y, ’. ’, color=’blue’, alpha=0.4, label=’Expectation(Kriging)’)
pl.scatter(u, z, color=’red ’, label=’Source data’)
pl.legend()
pl.show()
pl.close()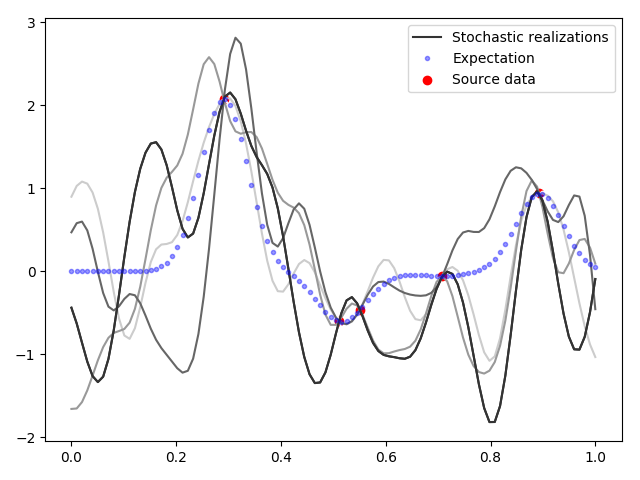
5.
5, . , , , , ( ). , , . — .
, , , (6). , , ( , , ).
, . , . . , , , — . , . — . , - 22 — . -5 , — - . , , , !
?
. (2D 3D), ( 1D ), , , numpy .
, , 6 «» -.
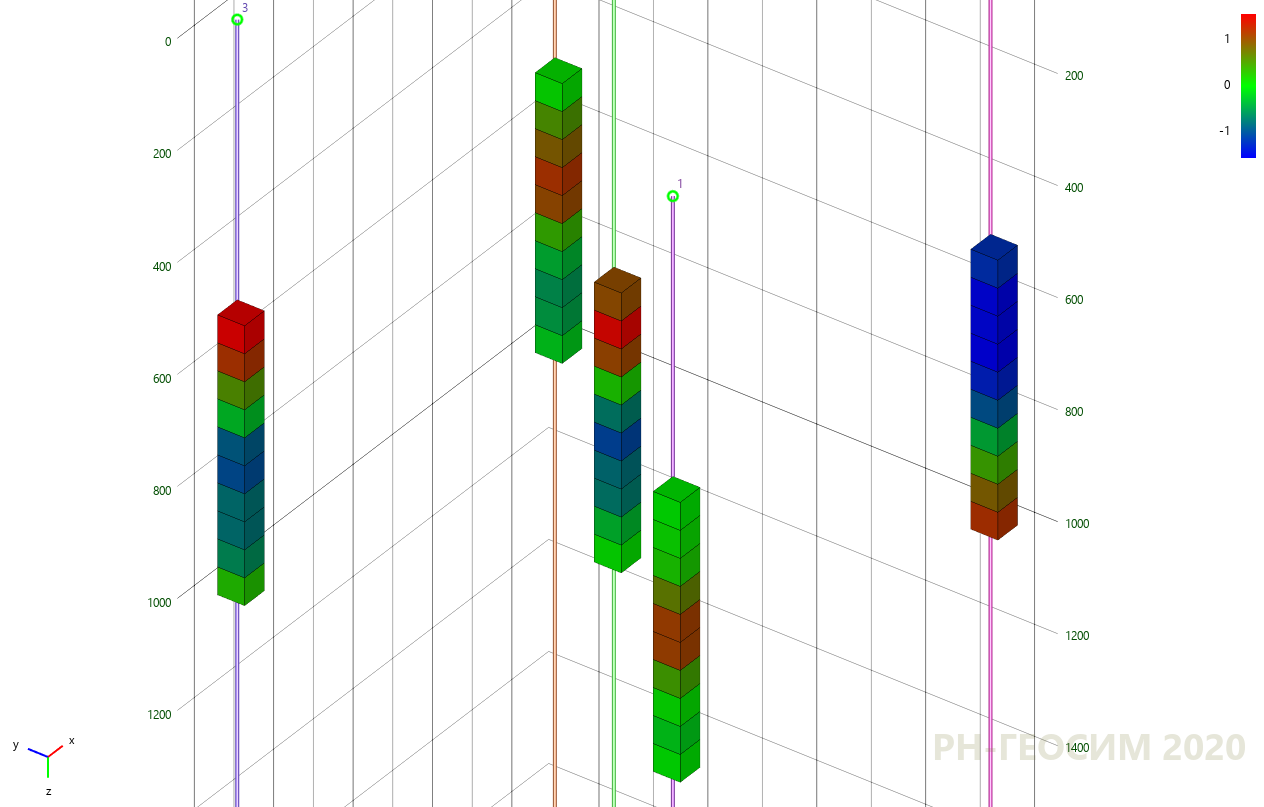
6. «» -
« ». , . (« ») (. 7) (. 8).
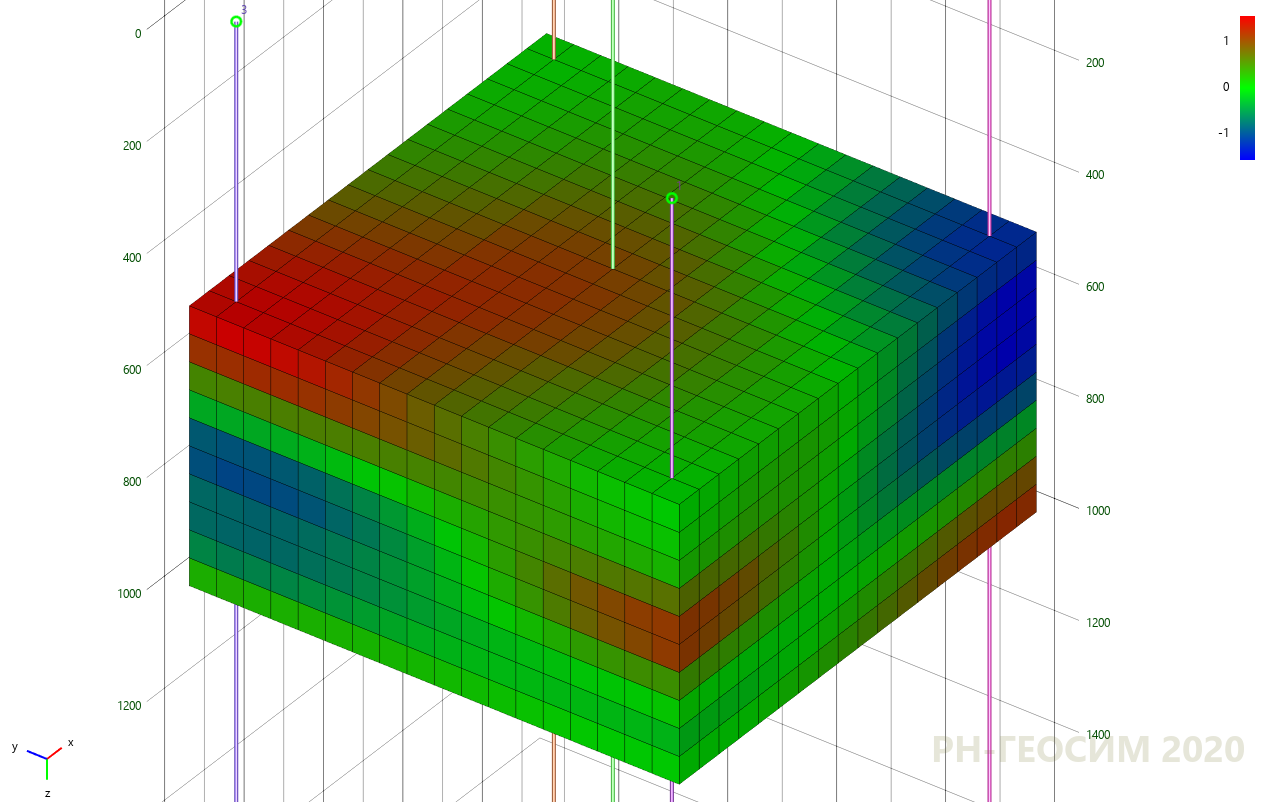
7. «» -

8. «» -
7 8 «» , , , «» .
«»
, . , «X» «Y», . 9.
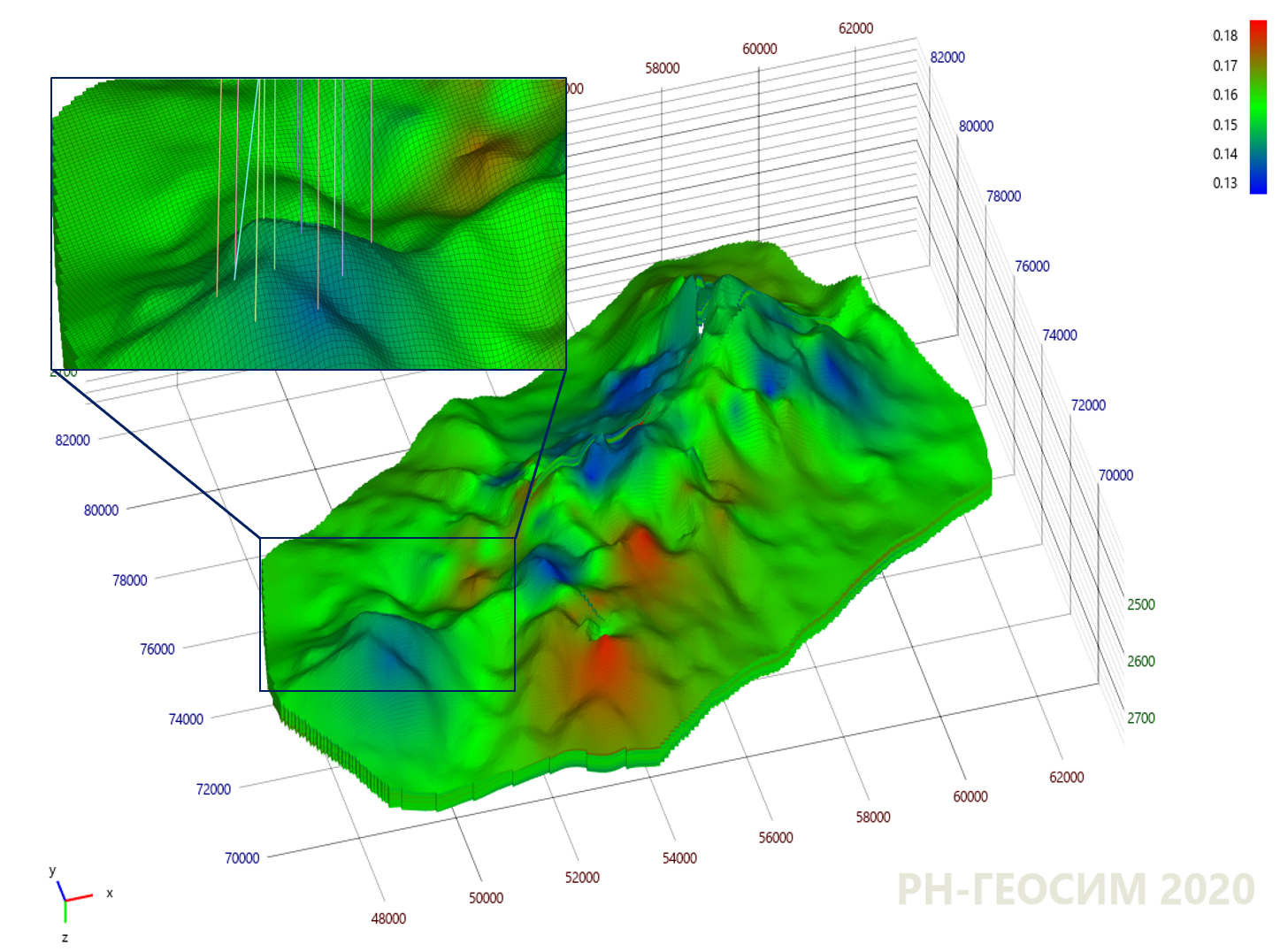
9. "X"
, . , , — ( ). (. . 10).

10. "X"
10 , , - .
, . . , . , .
, , , () , . . ( ), . . , ? , , , :
- ;
- ;
- , .
, - , , , , , , .