خوارزمية جونسون على دوغراف بأقواس سالبة

تم إعداد المقال عشية بدء دورة "الخوارزميات وهياكل البيانات"

---

تجد خوارزمية جونسون أقصر مسار بين جميع أزواج الرؤوس في رسم بياني موجه مرجح بأوزان سالبة بدون حدود سالبة.

أوه ، كيف يبدو! دعنا نحلل بيان المشكلة في أجزاء.

, , ( – ), . , 4 8 :

. «» «».

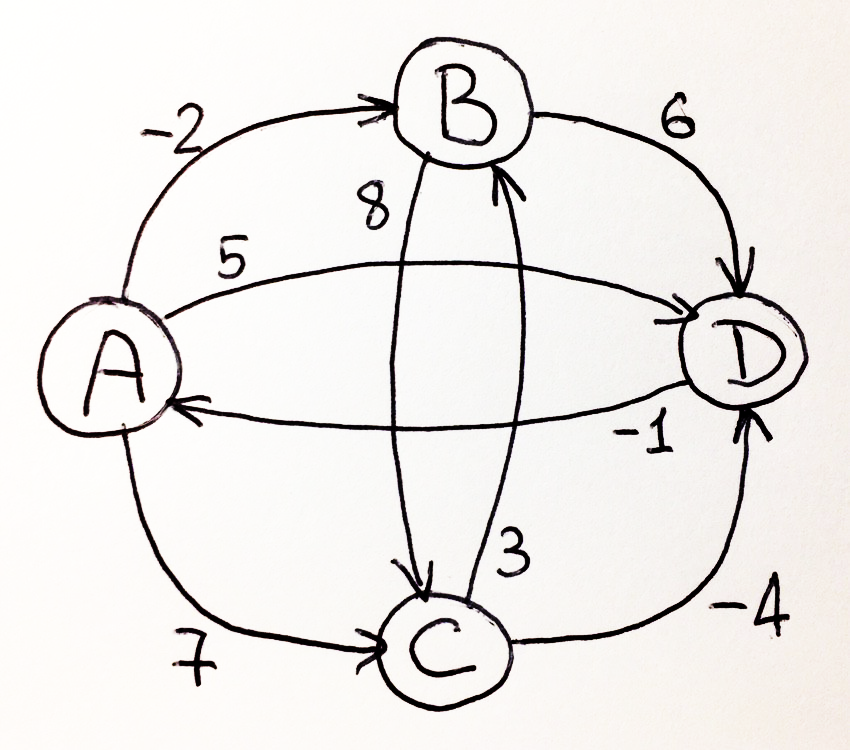
, «» «» . , . – . , D , .

, , , . . . «» «», , , .

, , , :

.

-, « » :

for k = 1 to n // n –    
    for x = 1 to n
        for y = 1 to n
            W[x][y] = min(W[x][y], W[x][k] + W[k][y])

W[x][y] .

W – . , .

«» . X Y , – .

- , – , – .

. , , , -.

, .

, , (-2), «» D (-2+6=4). . CD .

. , .

?

: ! : , , . !

?

– , . ? , .

, 4, A D : 5 + 1 * 4 = 9. 3 (A-B-C-D) 12 : -2 + 8 – 4 + 3 * 4 = 14.

, – , . ? XY h(X) h(Y), h(v) – «» , .

:

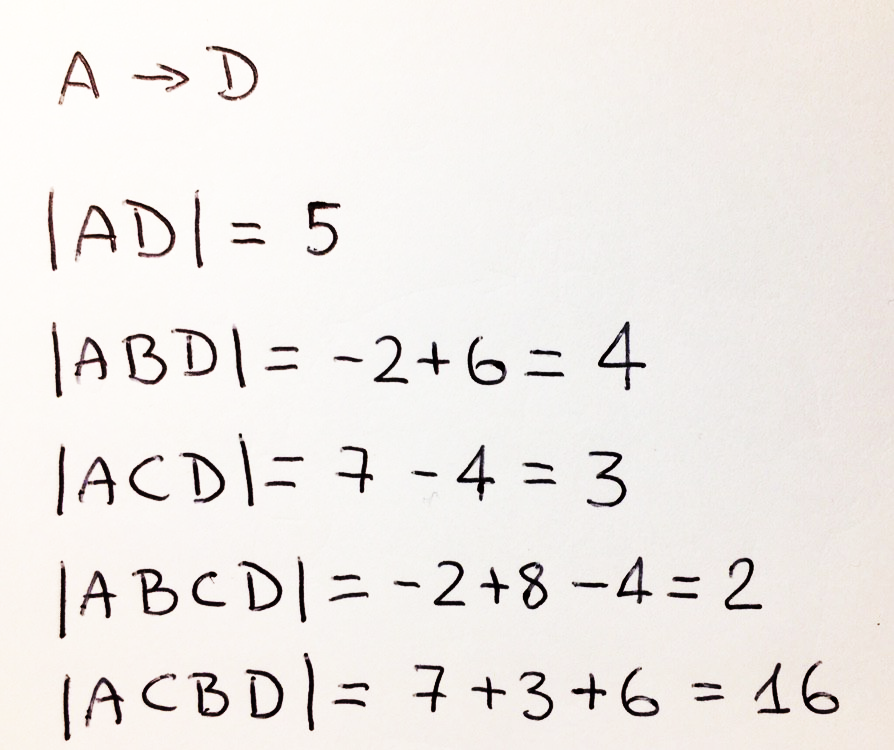, A D:

, A D , h(A) – h(D), , , ! , .

h, .

,

- S, . , S S* , S, «» .

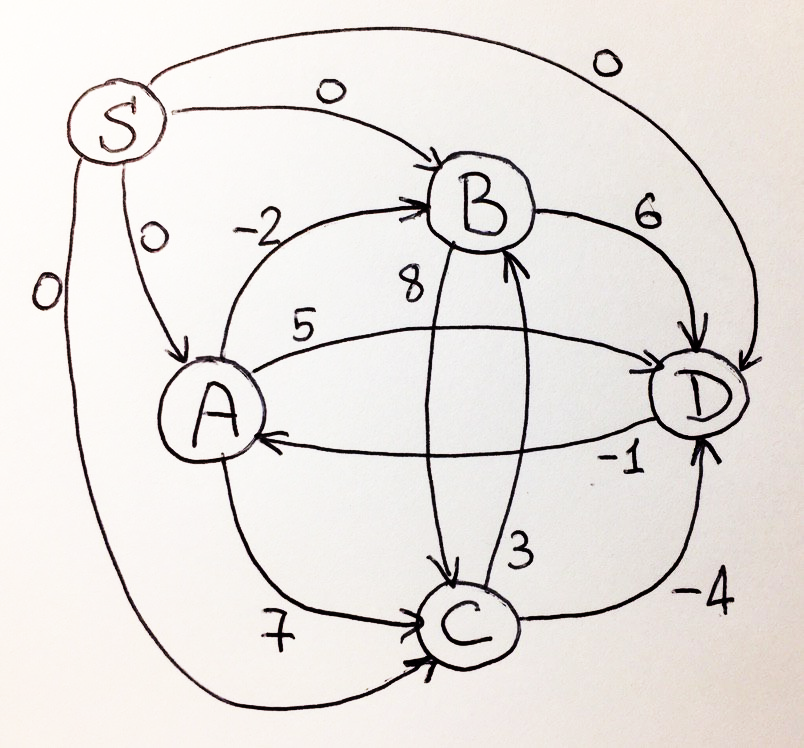
-, S . N «» S . «» , , :

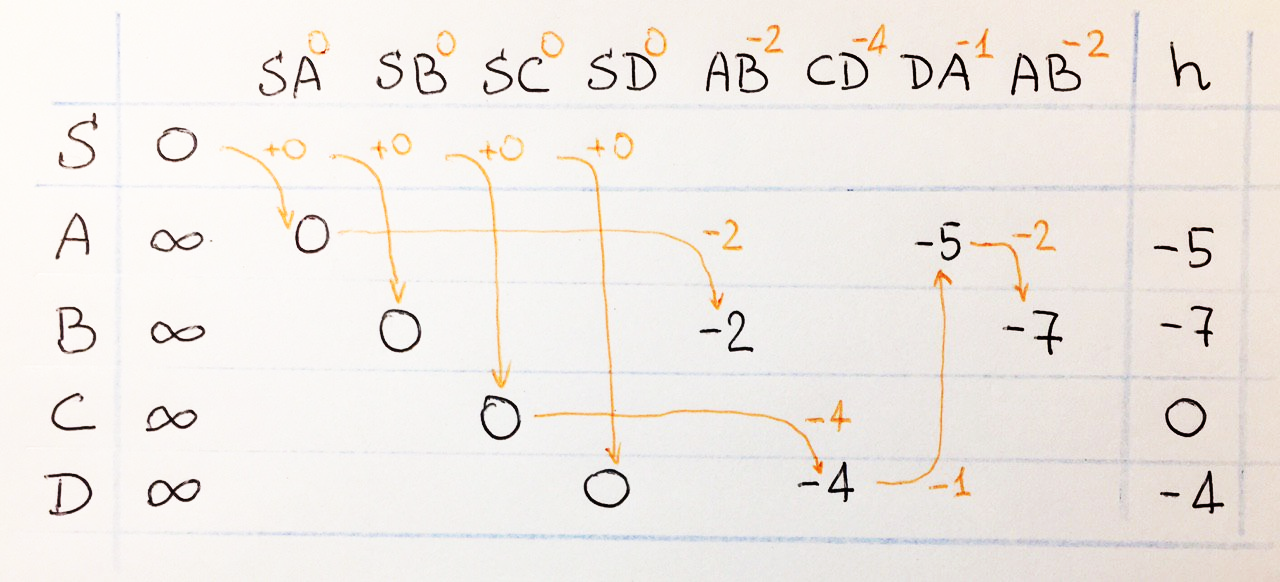
h . – S. S , h – . , , , , , , :

:

, , , ! .

, :

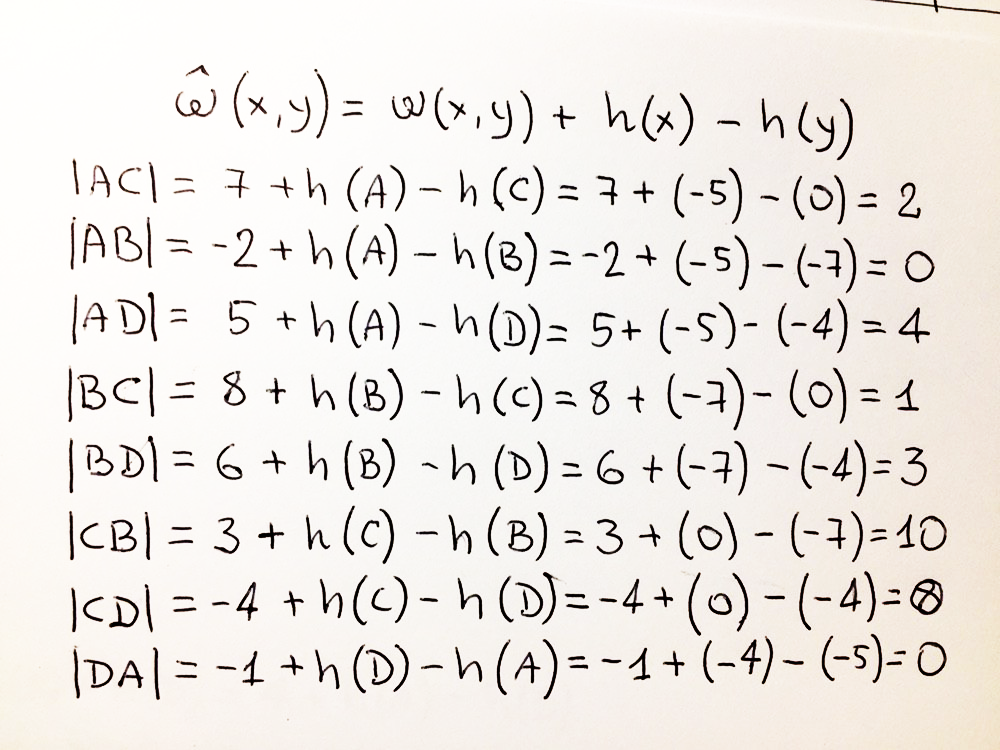
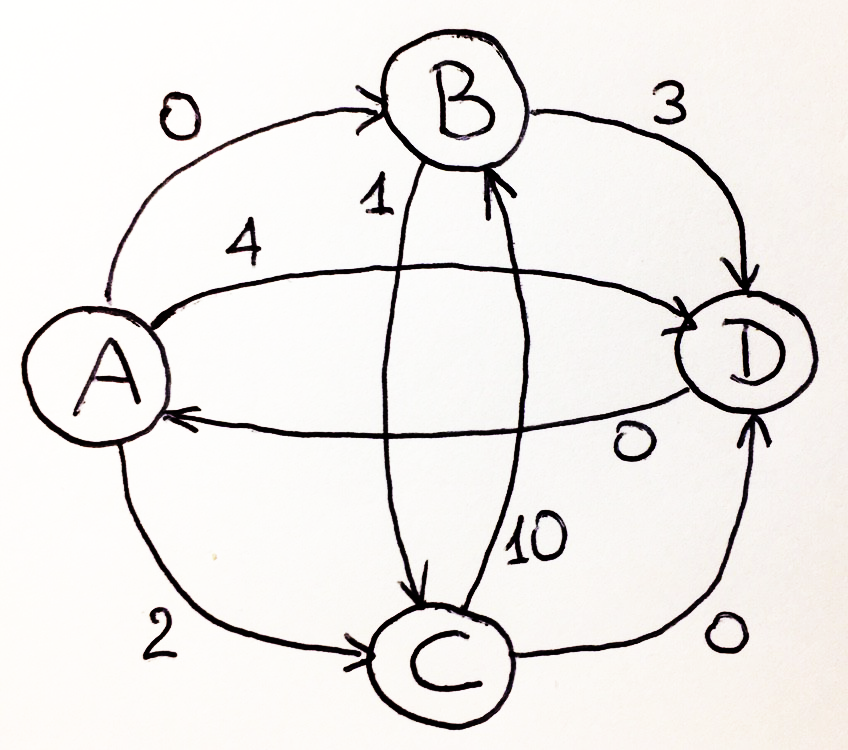
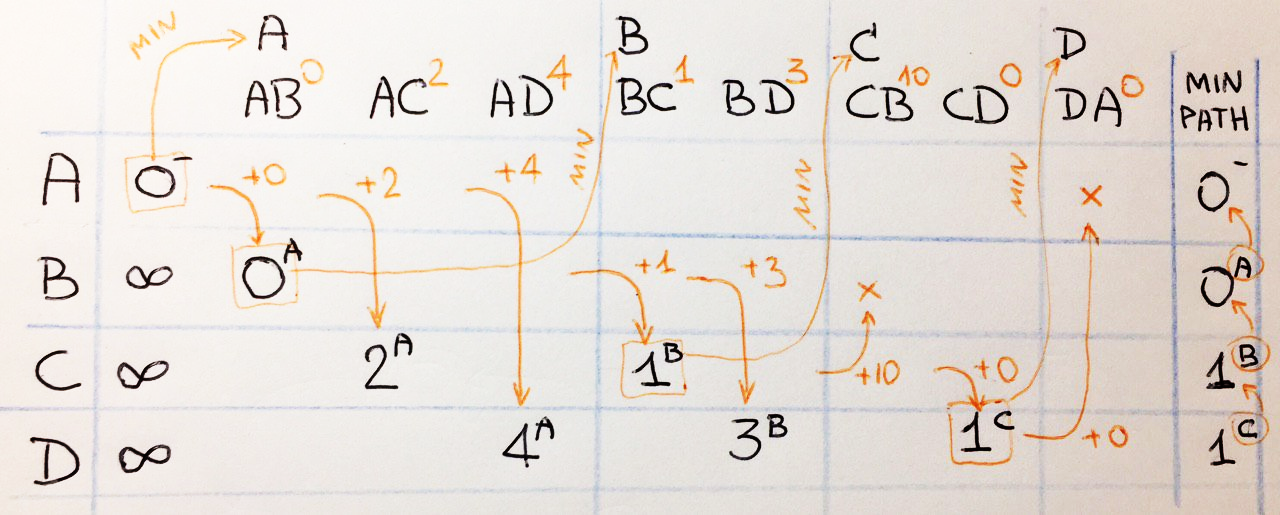
, , , . . , A D : A <= B <= C <= D, .

, . , .

---

« »

---