مرحبا زملائي! لم أكتب عن هبر منذ مائة عام ، لكن حان الوقت الآن. في ربيع هذا العام ، قمت بتدريس دورة تعلم الآلة المتقدمة في أكاديمية MADE Big Data Academy من مجموعة Mail.ru ؛ يبدو أن المستمعين أحبوا ذلك ، والآن طُلب مني ألا أكتب منشورًا إعلانيًا بقدر ما هو منشور تعليمي حول أحد مواضيع الدورة التدريبية الخاصة بي. كان الاختيار قريبًا من الواضح: كمثال على نموذج احتمالي معقد ، ناقشنا نموذجًا وبائيًا مناسبًا للغاية (على ما يبدو ... ولكن أكثر من ذلك لاحقًا) نموذج SIR الوبائي الذي يمثل انتشار الأمراض بين السكان. يحتوي على كل شيء: الاستدلال التقريبي من خلال أساليب ماركوف مونت كارلو ، ونماذج ماركوف المخفية باستخدام خوارزمية Viterbi العشوائية ، وحتى بيانات الحضور فقط.



مع هذا الموضوع ، ظهرت صعوبة واحدة صغيرة: بدأت في الكتابة عما قلته بالفعل وعرضته في المحاضرة ... وبطريقة ما بسرعة وبشكل غير محسوس ، تراكمت عشرون صفحة من النص (حسنًا ، بالصور والكود) ، والتي لم يتم بعد تم الانتهاء منه ولم يكن مكتفيًا بذاته على الإطلاق. وإذا أخبرت كل شيء بطريقة تجعله واضحًا من "الصفر" (وليس من الصفر المطلق بالطبع) ، فيمكنك كتابة مائة صفحة. لذلك سأكتبهم يومًا ما بالتأكيد ، لكنني الآن أقدم انتباهكم إلى الجزء الأول من وصف نموذج SIR ، حيث يمكننا فقط طرح مشكلة ووصف النموذج من جانبه المولِّد - وإذا كان للجمهور المحترم مصلحة ، فسيكون ذلك ممكنًا تقدم.

نموذج SIR: بيان المشكلة

أنا أحب أصدقائي وهم يحبونني ،

نحن أقرب ما يمكن أن نكون.

وفقط لأننا نهتم حقًا ،

كل ما نحصل عليه ، نشاركه!



توم ليرر. حصلت عليه من أغنيس

لذلك دعونا نفهم ذلك. بشكل غير رسمي ، الافتراضات الأساسية لنموذج SIR هي كما يلي:

• هناك مجموعة معينة من الناس يمكن أن يمشي فيها فيروس رهيب ؛
• في البداية ، يدخل الفيروس إلى السكان بطريقة أو بأخرى (على سبيل المثال ، يظهر المريض الأول) ، ثم يصاب الناس من بعضهم البعض ؛
• SIR , :
  
     ○ Susceptible ( , , .. ),
  
     ○ Infected ( )
  
     ○ Recovered ().

من أجل التبسيط ، سنفترض أن أولئك المرضى يطورون دائمًا مناعة ، ويتم استبعادهم من دورة الفيروس في الطبيعة. وفقًا لذلك ، يمكن أن تكون الانتقالات بين هذه الحالات فقط من اليسار إلى اليمين: حساس ← مصاب ← يتعافى.



المهمة ، في الواقع ، هي تدريب هذا النموذج ، أي فهم شيء ما حول معلمات عملية العدوى من البيانات. من السهل أن نفهم كيف تبدو البيانات - إنها ببساطة عدد المصابين المسجلين في كل لحظة زمنية ، والتي سنشير إليها بواسطة المتجه$$$\boldsymbol{y}$... على سبيل المثال ، عندما أعطيت واجبي المنزلي في الدورة التدريبية حول فيروس كورونا (مع ذلك ، كان يتعلق بنماذج أخرى) ، بدت البيانات الخاصة بروسيا كما يلي:

[2,2,2,2,3,4,6,8,10,10,10,10,15,20,25,30,45,59,63,93,114,147,199,253,306,438,438,495,658,840,1036,1264,1534,1836,2337,2777,3548,4149,4731,5389,6343,7497,8672]

لكن ما هي معلمات هذا النموذج ، وكيف تتفاعل مع بعضها البعض وكيفية تدريبها ، خاصة على مجموعة البيانات الصغيرة هذه ، هو سؤال أكثر جدية.



بشكل عام ، سأتبع المخطط العام للعمل ( Fintzi et al. ، 2016 ) ، الذي يبني خوارزميات MCMC لنماذج SIR و SEIR وبعض متغيراتها. ولكن بالمقارنة مع ( Fintzi et al.، 2016 ) ، سأقوم بتبسيط كل من النموذج وعرضه بشكل كبير. التبسيط الرئيسي هو أنه بدلاً من الوقت المستمر ، والذي تم اعتباره في العمل الأصلي ، سننظر في الوقت المنفصل ، أي بدلاً من العملية المستمرة التي تولد في مرحلة ما أحداثًا من النموذج "المصاب" و "المستعاد" ، سننظر في أن يمر الناس بمجموعة من النقاط المنفصلة في الوقت المناسب$$$t=1,\ldots,T$... سيسمح لنا هذا التبسيط ، أولاً ، بالتخلص من العديد من الصعوبات الفنية ، وثانيًا ، الانتقال من خوارزمية Metropolis-Hastings بشكل عام إلى خوارزمية أخذ عينات Gibbs ، أي عدم حساب نسبة Metropolis ، كما هو ضروري في ( Fintzi et آل ، 2016 ). إذا كنت لا تفهم ما قلته للتو ، فلا داعي للقلق: لن نحتاج إلى هذا اليوم ، وإذا كانت هناك أجزاء تالية ، فسأشرح كل شيء هناك.



سوف نشير إلى حالات نموذج SIR بواسطة S و I و R على التوالي وحالة الشخص$$$i$ في اللحظة $$$t$ - بجانب $$$x_i^{(t)}\in\{S, I, R\}$... في الوقت نفسه ، سنقدم على الفور متغيرات للعدد الإجمالي للمرضى الذين لم يمرضوا بعد.$$$S^{(t)}$مرض $$$I^{(t)}$ واستعادوا $$$R^{(t)}$ في اللحظة $$$t$... مجموع الرجل سيكون لدينا$$$N$لذلك لأي شخص $$$t$ سيتم إعدامه $$$S^{(t)} + I^{(t)} + R^{(t)} = N$... وكما كتبت أعلاه ،$$$y^{(t)}$منهم مسجلون (تم اختبارهم) مرضى.



المعلمات غير المعروفة للنموذج$$$\boldsymbol\theta = \{\beta, \mu, \rho, \boldsymbol{\pi}\}$أين:

• $$$\boldsymbol\pi$ - التوزيع الأولي للقضايا ؛ بعبارات أخرى،$$$x^{(1)}_j\sim \boldsymbol{\pi}$ لكل $$$j$؛ في نموذجنا المبسط ، لن نتدرب$$$\boldsymbol\pi$، ولكننا سنقوم ببساطة بتسجيل حالة واحدة إلى حالتين في اللحظة الأولى ؛
• $$$\rho$ - احتمال العثور على شخص مصاب في عموم السكان ، أي احتمال وجود شخص $$$x_j$ في هذه اللحظة $$$t$متى $$$x_j^{(t)}=I$، سيتم الكشف عنها عن طريق الاختبار والتسجيل في البيانات $$$y^{(t)}$؛ بمعنى آخر ، نقلب عملة معدنية لكل مريض لتحديد ما إذا كان الاختبار سيجدها أم لا ، بحيث يكون العنصر الحالي$$$y_t$ له توزيع ذو الحدين مع المعلمات $$$I^{(t)}$ و $$$\rho$:

  $$

  $$y^{(t)}\mid I^{(t)}, \rho \sim \mathrm{Binomial}(I^{(t)}, \rho);$$

• $$$\mu$ - احتمالية تعافي المريض في خطوة زمنية واحدة ، أي احتمال الانتقال من الحالة $$$I$ في الدولة $$$R$؛

و $$$\beta$ - هذه هي المعلمة الأكثر إثارة للاهتمام والتي توضح احتمالية الإصابة في وقت واحد من شخص مصاب . هذا يعني أنه في النموذج ، نفترض أن جميع الأشخاص في المجتمع "يتواصلون" مع بعضهم البعض ("الاتصال" هنا يعني الاتصال الكافي لنقل المرض ؛ ينتقل الفيروس التاجي بشكل أساسي عن طريق القطرات المحمولة جواً ، ولكن ، بالطبع ، من الممكن نمذجة و انتشار أي مرض آخر ؛ انظر ، على سبيل المثال ، النقوش) ، واحتمال الإصابة يعتمد على عدد المصابين الآن ، أي على ما هو$$$I^{(t)}$... سنفترض أبسط نموذج يكون فيه احتمال الإصابة من شخص مصاب$$$\beta$، وكل هذه الأحداث مستقلة ، مما يعني أن احتمالية البقاء بصحة جيدة

$$

$$(1-\beta)^{I^{(t)}}.$$

هذه الافتراضات في الواقع لديها الكثير للمناقشة. الشيء الأكثر إثارة للدهشة هنا ، في رأيي الشخصي ، هو التوزيع ذي الحدين لـ$$$y^{(t)}$... إن إلقاء عملة معدنية مع احتمال اكتشاف شخص مصاب أمر طبيعي تمامًا ، ولكن ليس من الواقعي أن نرمى هذه العملة مرة أخرى في كل خطوة ، أي أنه يمكننا "نسيان" شخص مصاب تم اكتشافه بالفعل. نتيجة لذلك ، يمكن لنموذج SIR (وغالبًا ما يفعل) إنتاج تسلسل غير رتيب تمامًا$$$\boldsymbol{y}$؛ هذا غريب ، لكن لا يبدو أن له تأثير كبير على النتيجة ، وسيكون من الأصعب بكثير نمذجة هذه العملية بشكل أكثر واقعية.



بالإضافة إلى ذلك ، من الواضح أن هذا النموذج مخصص لسكان مغلقين ، حيث "يتواصل" الجميع مع الجميع ، لذلك لا معنى لإطلاقه ، على سبيل المثال ، لروسيا باستخدام المعلمة N مائة مليون أو لموسكو مع المعلمة عشرة ملايين (و حسابيا لن تعمل). تم تخصيص اتجاه هام للامتدادات واستمرار نماذج SIR لهذا: كيفية إضافة رسم بياني أكثر واقعية للتفاعلات والالتهابات المحتملة ؛ سنتحدث على الأرجح عن هذا في آخر مشاركة أخيرة.



لكن مع كل هذه التبسيطات ، الآن ، باستخدام المعلمات المذكورة أعلاه ، يمكننا كتابة مصفوفة احتمالية الانتقال بين الحالات. تعتمد هذه الاحتمالات (على وجه التحديد ، على وجه التحديد ، احتمال الإصابة) على الإحصاءات العامة للسكان. دعونا نحدد متجه الحالات لجميع الناس باستثناء$$$x_j$، بجانب $$$\boldsymbol{x}_{-j}$، وتمديد نفس الترميز إلى جميع المتغيرات الأخرى ؛ على سبيل المثال ،$$$I_{-j}^{(t)}$ هو عدد المصابين في وقت واحد $$$t$، ناهيك عن $$$x_j$... ثم ، لاحتمالات الانتقال من$$$x_j^{(t-1)}$ في $$$x_j^{(t)}$ نحن نحصل

$$

$$p\left(x_j^{(t)}=S\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=S, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - (1 - \beta)^{I_{-j}^{(t-1)}},$$

$$

$$p\left(x_j^{(t)}=R\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = \mu,$$

$$

$$p\left(x_j^{(t)}=I\mid x_j^{(t-1)}=I, \boldsymbol{x}_{-j}^{(t-1)}\right) = 1 - \mu,$$

وفي جميع الحالات الأخرى

$$

$$p\left(x_j^{(t)}\mid x_j^{(t-1)}, \boldsymbol{x}_{-j}^{(t-1)}\right) = 0.$$

يمكن كتابة نفس الشيء بشكل أكثر وضوحًا في شكل مصفوفة احتمالية الانتقال (ترتيب الصفوف والأعمدة طبيعي ، SIR):

$$

$$\left(\begin{matrix} (1 - \beta)^{I_{-j}^{(t-1)}} & 1 - (1 - \beta)^{I_{-j}^{(t-1)}} & 0 \\ 0 & 1 - \mu & \mu \\ 0 & 0 & 1\end{matrix}\right)$$

بالنسبة للقارئ المطلع على سلاسل ماركوف ونماذج ماركوف ، قد يبدو أن هذا مجرد نموذج ماركوف مخفي: هناك حالة مخفية ، وهناك توزيع واضح للملاحظات لكل حالة مخفية ، والانتقالات هي ماركوف حقًا ، أي أن الحالة المخفية التالية تعتمد فقط على الحالة السابقة ... ولكن هناك كما يقولون ، هناك تحذير واحد: لا يمكن اعتبار احتمالات الانتقال ثابتة ، فهي تتغير مع التغيير $$$I^{(t)}$وهذا جانب أساسي للغاية من النموذج لا يمكن التخلص منه.



لذلك ، يصبح الاستدلال في هذا النموذج فجأة أكثر صعوبة مما هو عليه في نموذج ماركوف المخفي المعتاد (على الرغم من عدم وجود مثل هذه الهدية دائمًا). ومع ذلك ، على الرغم من أن الاستنتاج أكثر تعقيدًا ، إلا أنه لا يزال خاضعًا للعقل البشري - في التركيبات التالية (إن وجدت) سأخبرك فقط عن هذا. واليوم ، يكاد يكفي - الآن دعنا نسترخي قليلاً ونحاول اللعب بهذا النموذج في الوقت الحالي بمعنى توليدي.

مثال على توليد البيانات

كخبير وخبير كبير ،

دخل انطوائي في الحجر الصحي.

*** حاولت النحلة أن تشرح للديدان:

"لن أتمكن من العمل في المنزل"

.

***

مات كاجانوف وهو يمزح بمرح.

بالطبع ، أنا آسف جدًا له ، على الرغم من ...



ليونيد كاجانوف. الحجر الصحي

إذا كانت معلمات النموذج معروفة ، وتحتاج فقط إلى إنشاء مسار لكيفية تطور انتشار المرض بين السكان ، فلا يوجد شيء معقد في SIR. يُنشئ الكود أدناه مثالاً عن السكان وفقًا لنموذجنا ؛ الدول التي قمت بترميزها كـ$$$S=0$، $$$I=1$، $$$R=2$... كما حذرت ، من أجل البساطة سأفترض ذلك في الوقت الحالي$$$t=0$ هناك مريض واحد بالضبط من بين السكان ، ثم يستمر الأمر.

def sample_population(N, T, true_rho, true_beta, true_mu):
    true_log1mbeta = np.log(1 - true_beta)

    cur_states = np.zeros(N)
    cur_states[:1] = 1
    cur_I, test_y, true_statistics = 1, [1], [[N-1, 1, 0]]

    for t in range(T):
        logprob_stay_healthy = cur_I * true_log1mbeta
        for i in range(N):
            if cur_states[i] == 0 and np.random.rand() < -np.expm1(logprob_stay_healthy):
                cur_states[i] = 1
            elif cur_states[i] == 1 and np.random.rand() < true_mu:
                cur_states[i] = 2

        cur_I = np.sum(cur_states == 1)
        test_y.append( np.random.binomial( cur_I, true_rho ) )
        true_statistics.append([np.sum(cur_states == 0), np.sum(cur_states == 1), np.sum(cur_states == 2)])

    return test_y, np.array(true_statistics).T

N, T, true_rho, true_beta, true_mu = 100, 20, 0.1, 0.05, 0.1
test_y, true_statistics = sample_population(N, T, true_rho, true_beta, true_mu)

هذا الرمز لا يعطي البيانات الفعلية فقط $$$\boldsymbol{y}$ولكن أيضًا الإحصاءات "الحقيقية" $$$S^{(t)}$، $$$I^{(t)}$، $$$R^{(t)}$حتى يمكن تصورها. دعنا نقوم به؛ للمعلمات$$$N=100$، $$$T=20$، $$$\rho=0.1$، $$$\beta=0.2$، $$$\mu=0.3$يمكنك الحصول على شيء مثل هذا:







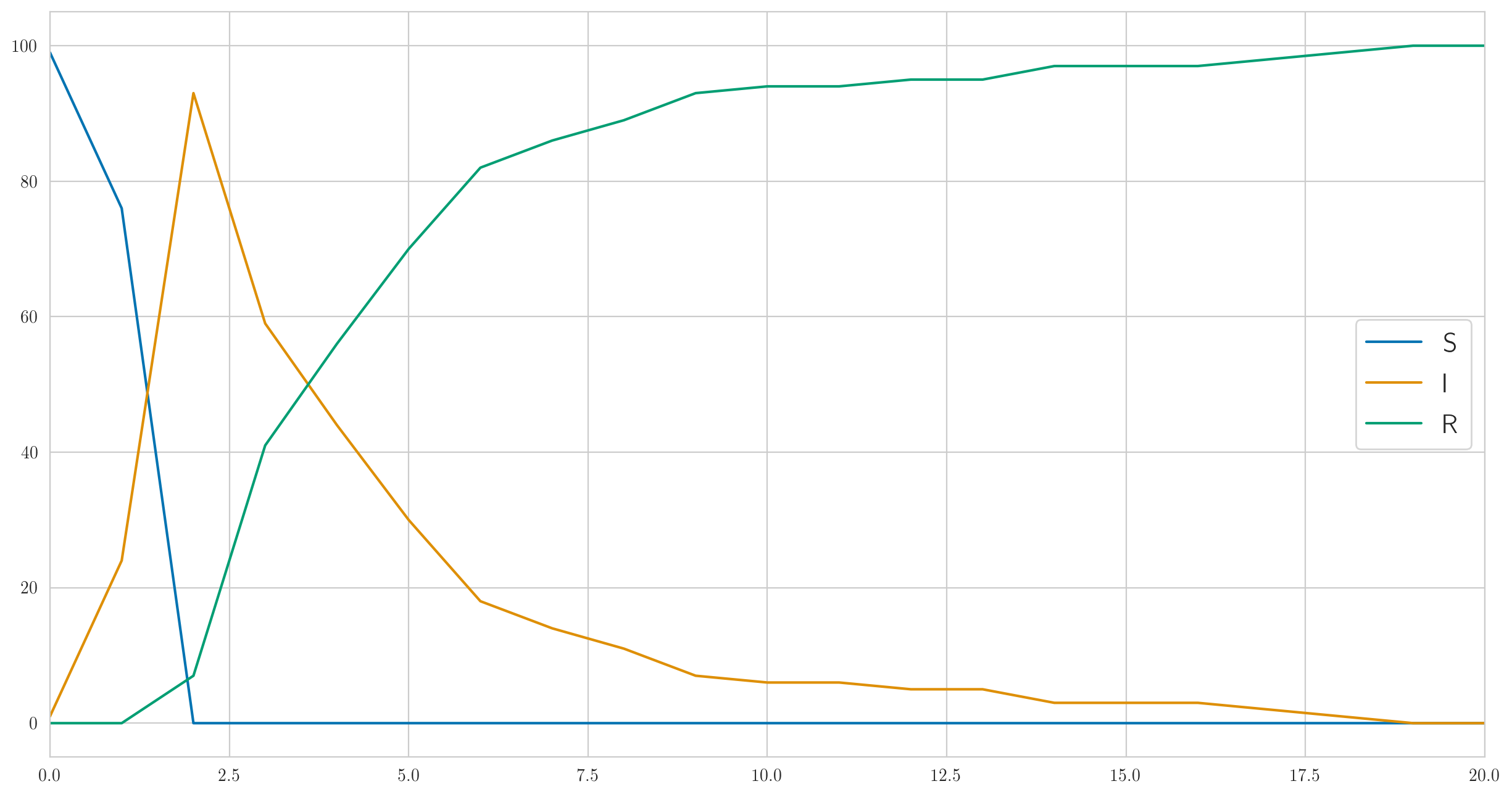
كما ترى ، في هذا المثال ، يمرض الجميع بسرعة كبيرة ، ثم يبدأ ببطء في التحسن وتبدو البيانات الفعلية المرصودة عن المرضى كما يلي:

[1 6 13 6 6 4 1 0 0 1 0 1 2 0 0 0 0 0 1 0 0]

لاحظ أنه ، كما ناقشنا أعلاه ، لا يوجد رتابة هنا.



لكن هذا بالتأكيد ليس السلوك الوحيد الممكن. لقد اخترت المعلمات أعلاه بحيث كانت العدوى سريعة بما فيه الكفاية وشمل المرض على الفور تقريبًا جميع الأشخاص المائة في مجتمع الاختبار لدينا. وإذا فعلت$$$\beta$ أصغر ، على سبيل المثال $$$\beta=0.01$عندها ستصبح العدوى أبطأ بكثير ، ولن يكون لدى الجميع وقت للمرض قبل أن يتعافى آخر مريض ولن يبقى. شيء من هذا القبيل:







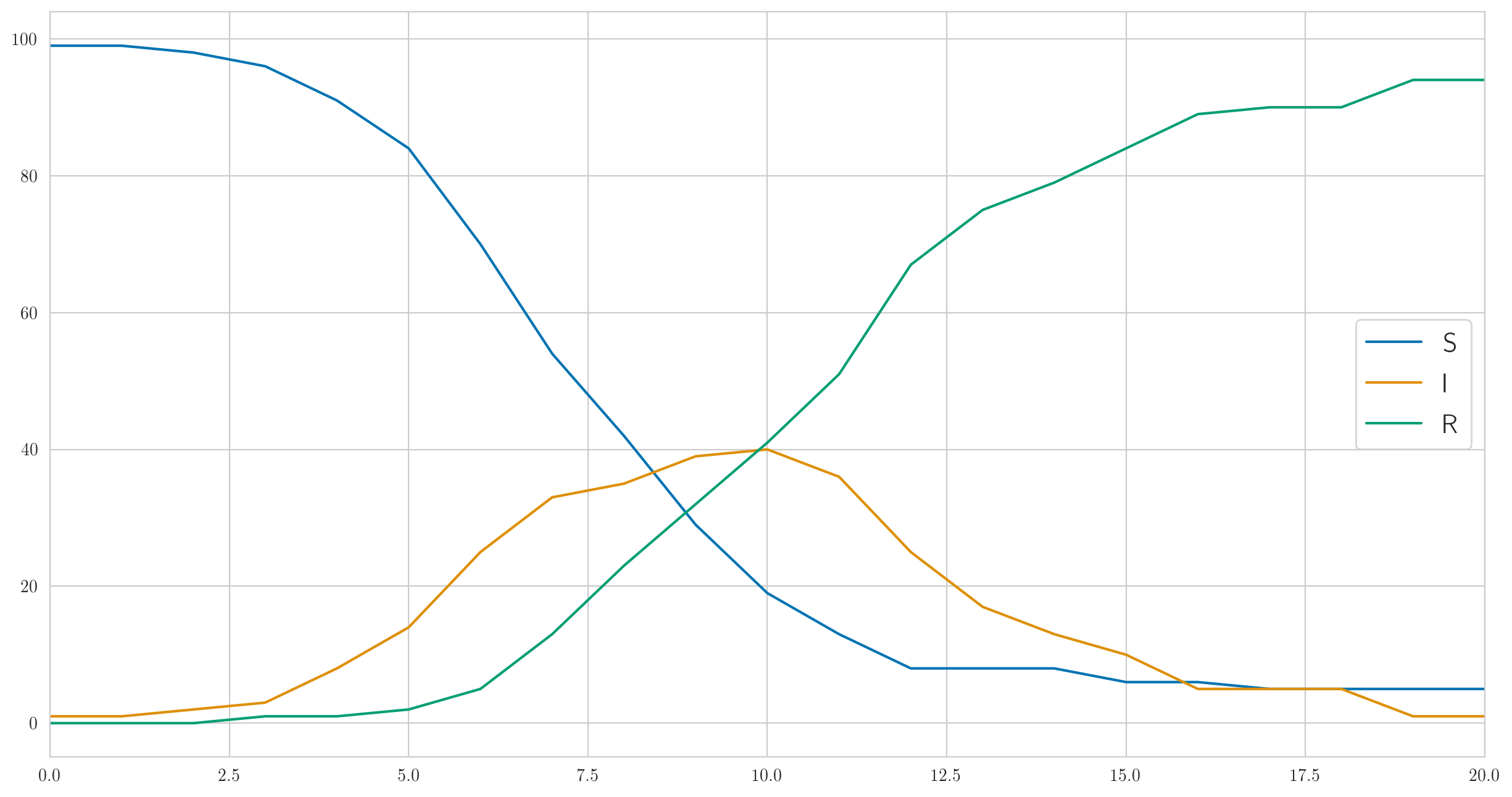
وعدد الحالات المكتشفة مختلف تمامًا أيضًا:

[1 0 0 0 0 1 2 2 3 1 1 9 3 1 3 1 0 1 0 0 0]

من الممكن "خنق" المرض أكثر ؛ على سبيل المثال ، دعنا نرحل$$$\beta=0.01$لكن ضع $$$\mu=0.5$، أي في كل فترة زمنية ، كل مريض لديه فرصة للتعافي بمقدار 0.5 (في النهاية ، هذا منطقي: إما أنه سوف يتعافى أم لا). عندها فقط 50-60 من كل 100 شخص سيصابون بالفيروس الرهيب ؛ يمكن أن تبدو المنحنيات كما يلي:

[1 0 0 1 3 2 1 1 0 3 0 0 0 0 0 1 0 0 0 0 0]

لكن الصورة العامة ، بالطبع ، تبدو متشابهة على أي حال: النمو الأسي الأول ، ثم الخروج إلى التشبع ؛ الاختلاف الوحيد هو ما إذا كان لدى آخر شركة نقل وقت للتعافي قبل إعادة تشغيل الجميع.



حسنًا ، حان الوقت لتلخيص النتائج المؤقتة. لقد رأينا اليوم كيف يبدو أحد أبسط النماذج الوبائية. على الرغم من مجموعة من الافتراضات المبالغة في التبسيط ، لا يزال نموذج SIR مفيدًا جدًا حتى في هذا الشكل ؛ الحقيقة هي أن معظم امتداداته واضحة إلى حد ما ولا تغير الجوهر العام للمسألة. لذلك ، إذا واصلنا ، في السلسلة التالية سأتحدث عن كيفية تدريب نموذج SIR ؛ ومع ذلك ، فإن هذا يستلزم الكثير من الأشياء المثيرة للاهتمام والتي ربما لن تناسبها في منشور واحد أيضًا. حتى المرة القادمة!