نقل الديناميات الجزيئية إلى CUDA. الجزء الثاني: تلخيص إيوالد

في مقال سابق ، ناقشنا أساس طريقة الديناميكيات الجزيئية ، بما في ذلك حساب قوى الطاقة والتفاعل بين الجسيمات ذات إمكانات زوجية معينة. ماذا لو كانت الجسيمات تحتوي على شحنة كهربائية؟ على سبيل المثال ، في حالة محاكاة بلورة من كلوريد الصوديوم ، تتكون من Na ⁺ و Cl ^- أيونات . أو محلول مائي يحتوي على أيونات معينة. في هذه الحالة ، بالإضافة إلى إمكانات الزوج من نوع Lennard-Jones ، تعمل القوى الإلكتروستاتيكية بين الأيونات ، أي قانون كولوم . طاقة هذا التفاعل لزوج من الجسيمات ij هي:

$$

$$E=C\frac{q_iq_j}{r_{ij}},$$

حيث q هي شحنة الجسيم ، و r _ij هي المسافة بين الجسيمات ، و C ثابتة بعض الشيء اعتمادًا على اختيار وحدات القياس. في SI هو -$$$\frac{1}{4\pi\epsilon_0}$، في SGS - 1 ، في برنامجي (حيث يتم التعبير عن الطاقة بجهد الإلكترون والمسافة في الأنجستروم والشحن في الشحنات الأولية) C تساوي تقريبًا 14.3996.







ماذا تقول؟ ما عليك سوى إضافة المصطلح المقابل إلى إمكانات الزوج وستنتهي. ومع ذلك ، في معظم الأحيان في نمذجة MD ، يتم استخدام شروط الحدود الدورية ، أي النظام المحاكي محاط من جميع الجهات بعدد لا نهائي من نسخه الافتراضية. في هذه الحالة ، ستتفاعل كل صورة افتراضية لنظامنا مع جميع الجسيمات المشحونة داخل النظام وفقًا لقانون كولوم. ونظرًا لأن تفاعل Coulomb ينقص بشكل ضعيف جدًا مع المسافة (مثل 1 / r) ، فإنه ليس من السهل استبعاده ، قائلين إننا لا نحسبه من هذه المسافة. تتباعد سلسلة من النموذج 1 / x ، أي يمكن لمقدارها ، من حيث المبدأ ، أن تنمو إلى أجل غير مسمى. والآن ، ألا تملحي وعاءً من الحساء؟ هل ستقتلك بالكهرباء؟



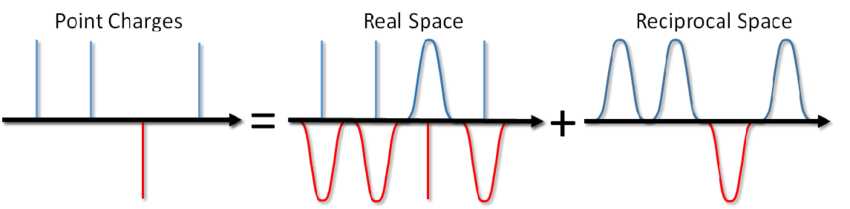
... لا يمكنك فقط ملح الحساء ، ولكن أيضًا حساب طاقة تفاعل كولوم في ظروف الحدود الدورية. تم اقتراح هذه الطريقة من قبل Ewald في عام 1921 لحساب طاقة البلورة الأيونية (يمكنك أيضًا رؤيتها على ويكيبيديا ). جوهر الطريقة هو فحص شحنات النقاط ثم طرح وظيفة الفحص. في هذه الحالة ، يتم تقليل جزء من التفاعل الكهروستاتيكي إلى قصير المفعول ويمكن قطعه ببساطة بطريقة قياسية. يتم تلخيص الجزء المتبقي بعيد المدى بشكل فعال في مساحة فورييه. مع حذف الاستنتاج ، الذي يمكن عرضه في مقالة Blinov أو في نفس الكتاب من قبل Frenkel و Smith ، سأكتب على الفور حلًا يسمى مجموع Ewald:

$$

$$E_{real} = \sum\limits^{N-1}_i{\sum\limits^N_{j=i+1}{ \frac{q_iq_j}{r_{ij}}\operatorname{erfc}(\alpha r_{ij}) }},$$

$$

$$E_{rec} = \frac{2\pi}{V}\sum_{\vec{k}\ne0}(\exp(-k^2/4\alpha^2)/k^2 \sum_jq_i\exp(i\vec{k}\vec{r}_j)),$$

$$

$$E_{const} = -\frac{C}{V\alpha} \sum_iq_i^2,$$

حيث α هي معلمة تنظم نسبة الحسابات في المساحات الأمامية والخلفية ، و k هي المتجهات في الفضاء المتبادل الذي يتم فيها الجمع ، V هو حجم النظام (في الفضاء الأمامي). الجزء الأول (E _real ) قصير المدى ويتم حسابه في نفس الدورة مثل إمكانات الزوج الأخرى ، راجع دالة real_ewald في المقالة السابقة. المساهمة الأخيرة (E _onst ) هي تصحيح للتفاعل الذاتي وغالبًا ما يطلق عليه "الجزء الثابت" لأنه لا يعتمد على إحداثيات الجسيمات. حسابه تافه ، لذلك سنركز فقط على الجزء الثاني من مجموع Ewald (E _rec) ، الجمع في الفضاء المتبادل. بطبيعة الحال ، في وقت اشتقاق Ewald ، لم يكن هناك ديناميكيات جزيئية ؛ لم أتمكن من العثور على من استخدم هذه الطريقة لأول مرة في MD. في الوقت الحاضر ، يحتوي أي كتاب عن MD على عرضه كنوع من المعيار الذهبي. ل كتاب، ألن حتى زودت رمز المثال في فورتران. لحسن الحظ ، لا يزال لدي الرمز الذي تم كتابته مرة واحدة في C للإصدار المتسلسل ، يبقى فقط موازنته (سمحت لنفسي بحذف بعض الإعلانات المتغيرة وتفاصيل أخرى غير مهمة):

void ewald_rec()
{
    int mmin = 0;
    int nmin = 1;

    //    iexp(x[i] * kx[l]),
    double** elc;
    double** els;
    //... iexp(y[i] * ky[m]) 
    double** emc;
    double** ems;
    //... iexp(z[i] * kz[n]),
    double** enc;
    double** ens;

    //     iexp(x*kx)*iexp(y*ky)
    double* lmc;
    double* lms;
    //   q[i] * iexp(x*kx)*iexp(y*ky)*iexp(z*kz)
    double* ckc;
    double* cks;

    //   
    eng = 0.0;
    for (i = 0; i < Nat; i++)   //   
    {
        // emc/s[i][0]  enc/s[i][0]     
        //   elc/s  , . 
        elc[i][0] = 1.0;
        els[i][0] = 0.0;

        // iexp(kr)
        sincos(twopi * xs[i] * ra, els[i][1], elc[i][1]);
        sincos(twopi * ys[i] * rb, ems[i][1], emc[i][1]);
        sincos(twopi * zs[i] * rc, ens[i][1], enc[i][1]);
    }

    //     emc/s[i][l] = iexp(y[i]*ky[l]) ,   
    for (l = 2; l < ky; l++)
        for (i = 0; i < Nat; i++)
        {
            emc[i][l] = emc[i][l - 1] * emc[i][1] - ems[i][l - 1] * ems[i][1];
            ems[i][l] = ems[i][l - 1] * emc[i][1] + emc[i][l - 1] * ems[i][1];
        }

    //     enc/s[i][l] = iexp(z[i]*kz[l]) ,   
    for (l = 2; l < kz; l++)
        for (i = 0; i < Nat; i++)
        {
            enc[i][l] = enc[i][l - 1] * enc[i][1] - ens[i][l - 1] * ens[i][1];
            ens[i][l] = ens[i][l - 1] * enc[i][1] + enc[i][l - 1] * ens[i][1];
        }

    //     K-:
    for (l = 0; l < kx; l++)
    {
        rkx = l * twopi * ra; 
        //  exp(ikx[l])  ikx[0]   
        if (l == 1)
            for (i = 0; i < Nat; i++)
            {
                elc[i][0] = elc[i][1];
                els[i][0] = els[i][1];
            }
        else if (l > 1)
            for (i = 0; i < Nat; i++)
            {
                // iexp(kx[0]) = iexp(kx[0]) * iexp(kx[1])
                x = elc[i][0];
                elc[i][0] = x * elc[i][1] - els[i][0] * els[i][1];
                els[i][0] = els[i][0] * elc[i][1] + x * els[i][1];
            }

        for (m = mmin; m < ky; m++)
        {
            rky = m * twopi * rb;
            //     iexp(kx*x[i]) * iexp(ky*y[i])
            if (m >= 0)
                for (i = 0; i < Nat; i++)
                {
                    lmc[i] = elc[i][0] * emc[i][m] - els[i][0] * ems[i][m];
                    lms[i] = els[i][0] * emc[i][m] + ems[i][m] * elc[i][0];
                }
            else //    m   :
                for (i = 0; i < Nat; i++)
                {
                    lmc[i] = elc[i][0] * emc[i][-m] + els[i][0] * ems[i][-m];
                    lms[i] = els[i][0] * emc[i][-m] - ems[i][-m] * elc[i][0];
                }

            for (n = nmin; n < kz; n++)
            {
                rkz = n * twopi * rc;
                rk2 = rkx * rkx + rky * rky + rkz * rkz;
                if (rk2 < rkcut2) //   
                {
                    //   (q[i]*iexp(kr[k]*r[i])) -  
                    sumC = 0; sumS = 0;
                    if (n >= 0)
                        for (i = 0; i < Nat; i++)
                        {
                            //  
                            ch = charges[types[i]].charge;

                            ckc[i] = ch * (lmc[i] * enc[i][n] - lms[i] * ens[i][n]);
                            cks[i] = ch * (lms[i] * enc[i][n] + lmc[i] * ens[i][n]);

                            sumC += ckc[i];
                            sumS += cks[i];
                        }
                    else //      :
                        for (i = 0; i < Nat; i++)
                        {
                            //  
                            ch = charges[types[i]].charge;

                            ckc[i] = ch * (lmc[i] * enc[i][-n] + lms[i] * ens[i][-n]);
                            cks[i] = ch * (lms[i] * enc[i][-n] - lmc[i] * ens[i][-n]);

                            sumC += ckc[i];
                            sumS += cks[i];
                        }

                    //    
                    akk = exp(rk2 * elec->mr4a2) / rk2;
                    eng += akk * (sumC * sumC + sumS * sumS);

                    for (i = 0; i < Nat; i++)
                    {
                        x = akk * (cks[i] * sumC - ckc[i] * sumS) * C * twopi * 2 * rvol;
                        fxs[i] += rkx * x;
                        fys[i] += rky * x;
                        fzs[i] += rkz * x;
                    }

                }
            } // end n-loop (over kz-vectors)

            nmin = 1 - kz;

        } // end m-loop (over ky-vectors)

        mmin = 1 - ky;

    }  // end l-loop (over kx-vectors)


   engElec2 = eng *  * twopi * rvol;
}

زوجان من التفسيرات للشفرة: تحسب الوظيفة الأس المعقد (في التعليقات على الكود يُشار إليه iexp لإزالة الوحدة الخيالية من الأقواس) من المنتج المتجه لـ k-vector ومتجه نصف القطر للجسيم لجميع ناقلات k وجميع الجسيمات. يتم ضرب هذا الأس في شحنة الجسيم. بعد ذلك ، يتم حساب مجموع هذه المنتجات لجميع الجسيمات (المجموع الداخلي في صيغة E _rec ) ، ويسمى في Frenkel كثافة الشحن ، وفي Blinov يطلق عليه العامل الهيكلي. وبعد ذلك ، على أساس هذه العوامل الهيكلية ، يتم حساب الطاقة والقوى التي تعمل على الجسيمات. تتميز مكونات المتجهات k (2π * l / a ، 2π * m / b ، 2π * n / c) بثلاثة أعداد صحيحة l ، m و n، والتي تعمل في دورات تصل إلى الحدود التي يحددها المستخدم. المعلمات a و b و c هي أبعاد النظام المحاكي في الأبعاد x و y و z على التوالي (الاستنتاج صحيح لنظام له هندسة مستطيلة متوازية). في الكود ، 1 / a و 1 / b و 1 / c تتوافق مع المتغيرات ra و rb و rc . يتم عرض صفائف كل قيمة في نسختين: للأجزاء الحقيقية والخيالية. يتم الحصول على كل متجه k التالي في بُعد واحد بشكل متكرر من البعد السابق عن طريق ضرب المركب السابق في واحد ، حتى لا يتم حساب الجيب مع جيب التمام في كل مرة. يتم ملء صفائف emc / s و enc / s لجميع مو n ، على التوالي ، ويضع المصفوفة elc / s القيمة لكل l > 1 في مؤشر الصفر لـ l لتوفير الذاكرة.



لغرض التوازي ، من المفيد "عكس" ترتيب الدورات بحيث تدور الدورة الخارجية فوق الجسيمات. وهنا نرى مشكلة - يمكن موازنة هذه الوظيفة فقط قبل حساب المجموع على جميع الجسيمات (كثافة الشحن). تستند الحسابات الإضافية إلى هذا المبلغ ، وسيتم حسابها فقط عندما تنتهي جميع سلاسل الرسائل من عملها ، لذا يجب عليك تقسيم هذه الوظيفة إلى قسمين. الأول يحسب كثافة الشحن ، والثاني يحسب الطاقة والقوى. لاحظ أن الوظيفة الثانية ستتطلب مرة أخرى الكمية q _iiexp (kr) لكل جسيم ولكل متجه k ، محسوب في الخطوة السابقة. وهنا يوجد نهجان: إما إعادة حسابه مرة أخرى ، أو تذكره.



الخيار الأول يستغرق المزيد من الوقت ، والثاني - ذاكرة أكبر (عدد الجسيمات * عدد المتجهات k * sizeof (float2)). استقرت على الخيار الثاني:

__global__ void recip_ewald(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the first part : summ (qiexp(kr)) evaluation
{
    int i;      // for atom loop
    int ik;     // index of k-vector
    int l, m, n;
    int mmin = 0;
    int nmin = 1;
    float tmp, ch;
    float rkx, rky, rkz, rk2;   // component of rk-vectors

    int nkx = md->nk.x;
    int nky = md->nk.y;
    int nkz = md->nk.z;
    
    // arrays for keeping iexp(k*r) Re and Im part
    float2 el[2];
    float2 em[NKVEC_MX];
    float2 en[NKVEC_MX];

    float2 sums[NTOTKVEC];          // summ (q iexp (k*r)) for each k
    extern __shared__ float2 sh_sums[];     // the same in shared memory

    float2 lm;     // temp var for keeping el*em
    float2 ck;     // temp var for keeping q * el * em * en (q iexp (kr))

    // invert length of box cell
    float ra = md->revLeng.x;
    float rb = md->revLeng.y;
    float rc = md->revLeng.z;

    if (threadIdx.x == 0)
        for (i = 0; i < md->nKvec; i++)
            sh_sums[i] = make_float2(0.0f, 0.0f);
    __syncthreads();

    for (i = 0; i < md->nKvec; i++)
        sums[i] = make_float2(0.0f, 0.0f);

    int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
    int N = min(id0 + atPerThread, md->nAt);

    ik = 0;
    for (i = id0; i < N; i++)
    {
        // save charge
        ch = md->specs[md->types[i]].charge;

        el[0] = make_float2(1.0f, 0.0f);    // .x - real part (or cos) .y - imagine part (or sin)
        
        em[0] = make_float2(1.0f, 0.0f);
        en[0] = make_float2(1.0f, 0.0f);

        // iexp (ikr)
        sincos(d_2pi * md->xyz[i].x * ra, &(el[1].y), &(el[1].x));
        sincos(d_2pi * md->xyz[i].y * rb, &(em[1].y), &(em[1].x));
        sincos(d_2pi * md->xyz[i].z * rc, &(en[1].y), &(en[1].x));

        // fil exp(iky) array by complex multiplication
        for (l = 2; l < nky; l++)
        {
             em[l].x = em[l - 1].x * em[1].x - em[l - 1].y * em[1].y;
             em[l].y = em[l - 1].y * em[1].x + em[l - 1].x * em[1].y;
        }

        // fil exp(ikz) array by complex multiplication
        for (l = 2; l < nkz; l++)
        {
             en[l].x = en[l - 1].x * en[1].x - en[l - 1].y * en[1].y;
             en[l].y = en[l - 1].y * en[1].x + en[l - 1].x * en[1].y;
        }

        // MAIN LOOP OVER K-VECTORS:
        for (l = 0; l < nkx; l++)
        {
            rkx = l * d_2pi * ra; 
            
            // move exp(ikx[l]) to ikx[0] for memory saving (ikx[i>1] are not used)
            if (l == 1)
                el[0] = el[1];
            else if (l > 1)
                {
                    // exp(ikx[0]) = exp(ikx[0]) * exp(ikx[1])
                    tmp = el[0].x;
                    el[0].x = tmp * el[1].x - el[0].y * el[1].y;
                    el[0].y = el[0].y * el[1].x + tmp * el[1].y;
                }

            //ky - loop:
            for (m = mmin; m < nky; m++)
            {
                rky = m * d_2pi * rb;

                //set temporary variable lm = e^ikx * e^iky
                if (m >= 0)
                {
                        lm.x = el[0].x * em[m].x - el[0].y * em[m].y; 
                        lm.y = el[0].y * em[m].x + em[m].y * el[0].x;
                }
                else // for negative ky give complex adjustment to positive ky:
                {
                        lm.x = el[0].x * em[-m].x + el[0].y * em[-m].y;
                        lm.y = el[0].y * em[-m].x - em[-m].x * el[0].x;
                }

                //kz - loop:
                for (n = nmin; n < nkz; n++)
                {
                    rkz = n * d_2pi * rc;
                    rk2 = rkx * rkx + rky * rky + rkz * rkz;
                    if (rk2 < md->rKcut2) // cutoff
                    {
                        // calculate summ[q iexp(kr)]   (local part)
                        if (n >= 0)
                         {
                                ck.x = ch * (lm.x * en[n].x - lm.y * en[n].y);
                                ck.y = ch * (lm.y * en[n].x + lm.x * en[n].y);
                         }
                        else // for negative kz give complex adjustment to positive kz:
                         {
                                ck.x = ch * (lm.x * en[-n].x + lm.y * en[-n].y);
                                ck.y = ch * (lm.y * en[-n].x - lm.x * en[-n].y);
                        }
                        sums[ik].x += ck.x;
                        sums[ik].y += ck.y;
                        
                        // save qiexp(kr) for each k for each atom:
                        md->qiexp[i][ik] = ck;
                        ik++;
                    }
                } // end n-loop (over kz-vectors)

                nmin = 1 - nkz;

            } // end m-loop (over ky-vectors)
            mmin = 1 - nky;
        }  // end l-loop (over kx-vectors)
    } // end loop by atoms

    // save sum into shared memory
    for (i = 0; i < md->nKvec; i++)
    {
        atomicAdd(&(sh_sums[i].x), sums[i].x);
        atomicAdd(&(sh_sums[i].y), sums[i].y);
    }
    __syncthreads();

    //...and to global
    int step = ceil((double)md->nKvec / (double)blockDim.x);
    id0 = threadIdx.x * step;
    N = min(id0 + step, md->nKvec);
    for (i = id0; i < N; i++)
    {
        atomicAdd(&(md->qDens[i].x), sh_sums[i].x);
        atomicAdd(&(md->qDens[i].y), sh_sums[i].y);
    }
}
// end 'ewald_rec' function

__global__ void ewald_force(int atPerBlock, int atPerThread, cudaMD* md)
// calculate reciprocal part of Ewald summ
// the second part : enegy and forces
{
    int i;      // for atom loop
    int ik;     // index of k-vector
    float tmp;

    // accumulator for force components
    float3 force;

    // constant factors for energy and force
    float eScale = md->ewEscale;
    float fScale = md->ewFscale;

    int id0 = blockIdx.x * atPerBlock + threadIdx.x * atPerThread;
    int N = min(id0 + atPerThread, md->nAt);
    for (i = id0; i < N; i++)
    {
        force = make_float3(0.0f, 0.0f, 0.0f);

        // summ by k-vectors
        for (ik = 0; ik < md->nKvec; ik++)
        {
            tmp = fScale * md->exprk2[ik] * (md->qiexp[i][ik].y * md->qDens[ik].x - md->qiexp[i][ik].x * md->qDens[ik].y);

            force.x += tmp * md->rk[ik].x;
            force.y += tmp * md->rk[ik].y;
            force.z += tmp * md->rk[ik].z;
        }

        md->frs[i].x += force.x;
        md->frs[i].y += force.y;
        md->frs[i].z += force.z;
    } // end loop by atoms


    // one block calculate energy
    if (blockIdx.x == 0)
        if (threadIdx.x == 0)
        {
            for (ik = 0; ik < md->nKvec; ik++)
                md->engCoul2 += eScale * md->exprk2[ik] * (md->qDens[ik].x * md->qDens[ik].x + md->qDens[ik].y * md->qDens[ik].y);
        }

}
// end 'ewald_force' function

آمل أن تسامحني لترك التعليقات باللغة الإنجليزية ، فالشفرة هي نفسها النسخة التسلسلية تقريبًا. أصبح الكود أكثر قابلية للقراءة بسبب حقيقة أن المصفوفات فقدت بعدًا واحدًا: elc / s [i] [l] و emc / s [i] [m] و enc / s [i] [n] تحولت إلى بُعد واحد ، el و em و ar ، صفائف lmc / s و ckc / s - في المتغيرات lm و ck (اختفى البعد بالجسيمات ، حيث لم تعد هناك حاجة لتخزينه لكل جسيم ، يتم تجميع النتيجة الوسيطة في الذاكرة المشتركة). لسوء الحظ ، نشأت مشكلة على الفور: المصفوفات em و enيجب أن يكون ثابتًا حتى لا يتم استخدام الذاكرة العامة ولا يتم تخصيص الذاكرة ديناميكيًا في كل مرة. يتم تحديد عدد العناصر فيها من خلال توجيه NKVEC_MX (الحد الأقصى لعدد المتجهات k في بُعد واحد) في مرحلة التجميع ، ويتم استخدام العناصر nky / z الأولى فقط في وقت التشغيل. بالإضافة إلى ذلك ، ظهر مؤشر شامل لجميع المتجهات k وتوجيه مماثل ، مما يحد من العدد الإجمالي لهذه المتجهات NTOTKVEC . ستنشأ المشكلة إذا كان المستخدم يحتاج إلى المزيد من المتجهات k أكثر من المحدد في التوجيهات. لحساب الطاقة ، يتم توفير كتلة بمؤشر صفر ، حيث لا يهم أي كتلة ستقوم بإجراء هذا الحساب وبأي ترتيب. لاحظ أن القيمة المحسوبة في المتغير akkيعتمد الرمز التسلسلي فقط على حجم النظام المحاكي ويمكن حسابه في مرحلة التهيئة ، وفي تنفيذه يتم تخزينه في الصفيف md-> exprk2 [] لكل k-vector. وبالمثل ، تؤخذ مكونات ناقلات k من صفيف md-> rk [] . هنا قد يكون من الضروري استخدام وظائف FFT الجاهزة ، حيث تعتمد الطريقة عليها ، ولكن ما زلت لا أعرف كيفية القيام بذلك.



حسنًا ، الآن دعنا نحاول حساب شيء ما ، ولكن نفس كلوريد الصوديوم. لنأخذ ألفي أيون صوديوم ونفس الكمية من الكلور. دعونا نضع الرسوم على أنها أعداد صحيحة ، ونأخذ إمكانات الزوج ، على سبيل المثال ، من هذا العمل... لنقم بضبط تهيئة البداية بشكل عشوائي ونمزجها قليلاً ، الشكل 2 أ. نختار حجم النظام بحيث يتوافق مع كثافة كلوريد الصوديوم في درجة حرارة الغرفة (2.165 جم / سم ³ ). دعونا نبدأ كل هذا لفترة قصيرة (10 آلاف خطوة من 5 فيمتوثانية) مع مراعاة ساذجة للإلكتروستاتيكيات وفقًا لقانون كولوم وباستخدام جمع إيوالد. تظهر التشكيلات الناتجة في الشكلين 2 ب و 2 ج على التوالي. يبدو أنه في حالة إيوالد ، فإن النظام أكثر انسيابية قليلاً من دونه. من المهم أيضًا أن تكون تقلبات الطاقة الإجمالية قد انخفضت بشكل كبير مع استخدام الجمع.





الشكل 2 الشكل 2. التكوين الأولي لنظام NaCl (أ) وبعد خطوات التكامل 10،000: طريقة ساذجة (ب) ومع مخطط Ewald (ج).

بدلا من الاستنتاج

لاحظ أن البنية التي تم الحصول عليها في الشكل لا تتوافق مع الشبكة البلورية NaCl ، بل بالأحرى مع شبكة ZnS ، ولكن هذه بالفعل شكوى حول إمكانات الزوج. إن مراعاة الكهرباء الساكنة أمر مهم للغاية لنمذجة الديناميكيات الجزيئية. يعتقد أن التفاعل الإلكتروستاتيكي هو المسؤول عن تكوين المشابك البلورية ، حيث يعمل على مسافات كبيرة. صحيح ، من هذا الموقف ، من الصعب شرح كيفية تبلور مواد مثل الأرجون أثناء التبريد.



بالإضافة إلى طريقة إيوالد المذكورة ، هناك أيضًا طرق أخرى لمحاسبة الكهرباء الساكنة ، انظر ، على سبيل المثال ، هذه المراجعة .