🙇 ⌛️ 👨🏼‍🎓 رموز التصحيح. بداية نظرية ترميز جديدة 🤥 ⛎ 🚣🏿

تتطلب مشاكل أمن المعلومات دراسة وحل عدد من المشاكل النظرية والعملية في تفاعل المعلومات لمشتركي النظام. يصوغ مبدأ أمن المعلومات لدينا المهمة الثلاثية المتمثلة في ضمان سلامة المعلومات وسريتها وتوافرها. المقالات المقدمة هنا مكرسة للنظر في قضايا محددة لحلها في إطار أنظمة الدولة المختلفة والأنظمة الفرعية. في وقت سابق ، نظر المؤلف في 5 مقالات في قضايا ضمان سرية الرسائل من خلال معايير الدولة. أعطيت المفهوم العام للنظام الترميز أيضا لي في وقت سابق .

المقدمة

من خلال تعليمي الأساسي ، فأنا لست عالم رياضيات ، ولكن فيما يتعلق بالتخصصات التي قرأتها في الجامعة ، كان علي أن أفهمها بدقة. لوقت طويل وبإصرار قرأت الكتب المدرسية الكلاسيكية لجامعاتنا الرائدة ، موسوعة رياضية من خمسة مجلدات ، والعديد من الكتيبات الشعبية الرفيعة حول قضايا معينة ، لكن لم يرضي الرضا. لم ينشأ الفهم العميق للقراءة أيضًا.

تركز جميع الكلاسيكيات الرياضية ، كقاعدة عامة ، على الحالة النظرية اللانهائية ، وتستند التخصصات الخاصة إلى حالة الإنشاءات المحدودة والهياكل الرياضية. الاختلاف في المناهج هائل ، وربما يكون غياب أو عدم وجود أمثلة كاملة جيدة هو العيب الرئيسي ونقص الكتب المدرسية الجامعية. نادرًا ما يوجد كتاب إشكالي يحتوي على حلول للمبتدئين (للطلاب الجدد) ، وتلك الموجودة بالفعل تعتبر خطيئة في الإغفال في التفسيرات. بشكل عام ، لقد وقعت في حب متاجر الكتب التقنية المستعملة ، والتي بفضلها تم تجديد المكتبة ، وإلى حد ما ، مخزن المعرفة. سنحت لي الفرصة لقراءة الكثير ، الكثير ، لكن "لم أذهب".

قادني هذا المسار إلى السؤال ، ماذا يمكنني أن أفعل بمفردي بدون "عكازات" للكتب ، أمامي فقط ورقة بيضاء وقلم رصاص بممحاة؟ اتضح أن الأمر قليل جدًا وليس تمامًا ما هو مطلوب. لقد تم اجتياز الطريق الصعب المتمثل في التعليم الذاتي العشوائي. كان السؤال هذا. هل يمكنني بناء وشرح ، أولاً وقبل كل شيء لنفسي ، عمل الكود الذي يكتشف الأخطاء ويصلحها ، على سبيل المثال ، كود هامينج ، (7 ، 4) - كود؟

من المعروف أن كود Hamming يستخدم على نطاق واسع في العديد من التطبيقات في مجال تخزين البيانات وتبادلها ، وخاصة في RAID ؛ بالإضافة إلى ذلك ، فهو موجود في ذاكرة ECC ويسمح بالتصحيح السريع للأخطاء الفردية والمزدوجة.

أمن المعلومات. الرموز والأصفار ورسائل Steg

يجب توفير الحماية لتفاعل المعلومات من خلال تبادل الرسائل بين المشاركين فيها على مستويات مختلفة وبوسائل مختلفة ، سواء من الأجهزة والبرامج. تم تطوير وتصميم وإنشاء هذه الأدوات في إطار بعض النظريات (انظر الشكل أ) والتقنيات المعتمدة من قبل الاتفاقيات الدولية بشأن نماذج OSI / ISO.

أصبحت حماية المعلومات في أنظمة اتصالات المعلومات (ITS) عمليا المشكلة الرئيسية في حل مشاكل الإدارة ، سواء على مستوى الفرد - المستخدم ، أو بالنسبة للشركات والجمعيات والإدارات والدولة ككل. من بين جميع جوانب حماية ITKS ، سننظر في هذه المقالة في حماية المعلومات أثناء استخراجها ومعالجتها وتخزينها ونقلها في أنظمة الاتصالات.

لمزيد من التوضيح لمجال الموضوع ، سنركز على اتجاهين محتملين حيث يتم النظر في نهجين مختلفين لحماية المعلومات وعرضها واستخدامها: نحوي ودلالي. يتم استخدام الاختصارات التالية في الشكل: الترميز - الترميز - وحدة فك الترميز ؛ shidesh - جهاز فك التشفير. صرير - كونسيلر - مستخرج.

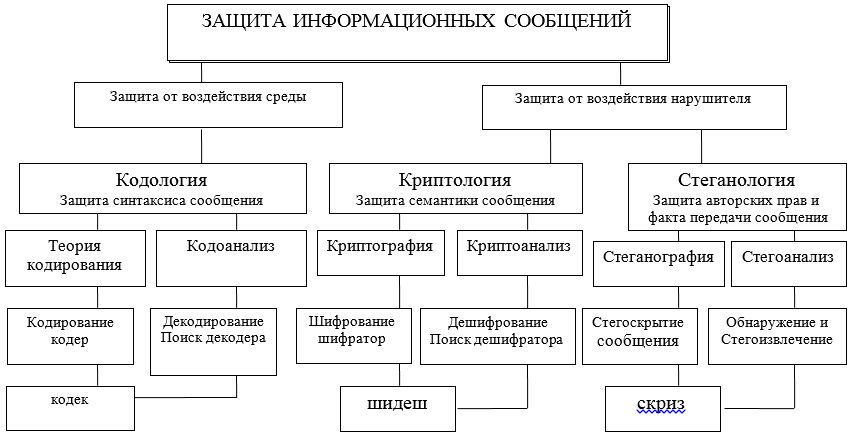
الشكل أ - رسم تخطيطي للاتجاهات الرئيسية والعلاقات المتبادلة للنظريات التي تهدف إلى حل مشاكل حماية تفاعل المعلومات تسمح لك

الميزات النحوية لعرض الرسائل بالتحكم والتأكد من صحة ودقة العرض التقديمي (خالية من الأخطاء ، وسلامة) أثناء التخزين والمعالجة ، وخاصة عند نقل المعلومات عبر قنوات الاتصال. هنا ، يتم حل المشاكل الرئيسية للحماية من خلال طرق علم الكود ، وجزء كبير منه - نظرية تصحيح الرموز.

الأمن الدلالي (الدلالي)يتم توفير الرسائل من خلال أساليب التشفير ، والتي تتيح لك عن طريق التشفير الحماية من إتقان محتوى المعلومات من قبل متطفل محتمل. وفي الوقت نفسه ، يمكن للمخالف نسخ أو سرقة أو تغيير أو استبدال أو حتى إتلاف الرسالة وناقلها ، لكنه لن يتمكن من الحصول على معلومات حول محتوى الرسالة المرسلة ومعناها. سيظل محتوى المعلومات الواردة في الرسالة غير قابل للوصول إلى الجاني. وبالتالي ، سيكون موضوع مزيد من الدراسة هو الحماية النحوية والدلالية للمعلومات في ITCS. في هذه المقالة ، سنقتصر على التفكير في النهج النحوي فقط في تنفيذ بسيط ولكنه مهم جدًا من خلال تصحيح التعليمات البرمجية.

سأقوم على الفور برسم خط فاصل في حل مشاكل أمن المعلومات:

نظرية الكودمصمم لحماية المعلومات (الرسائل) من الأخطاء (حماية وتحليل تركيب الرسائل) للقناة والبيئة ، لاكتشاف الأخطاء وتصحيحها ؛ تم تصميم

نظرية علم التشفير لحماية المعلومات من الوصول غير المصرح به إلى دلالاتها من قبل الدخيل (حماية الدلالات ، معنى الرسائل) ؛ تم تصميم

نظرية علم الإخفاء لحماية حقيقة تبادل المعلومات للرسائل ، وكذلك لحماية حقوق النشر والبيانات الشخصية (حماية السرية الطبية).

بشكل عام ، دعنا نذهب. بحكم التعريف ، وهناك عدد غير قليل منهم ، ليس من السهل فهم وجود رمز. يكتب المؤلفون أن الكود عبارة عن خوارزمية وعرض وشيء آخر. لن أكتب عن تصنيف الأكواد هنا ، سأقول فقط أن الكود (7 ، 4) هو بلوك .

في مرحلة ما ، اتضح لي أن الكود عبارة عن كلمات رمزية خاصة ، مجموعة محدودة منها ، يتم استبدالها بخوارزميات خاصة بالنص الأصلي للرسالة على جانب الإرسال من قناة الاتصال والتي يتم إرسالها عبر القناة إلى جهاز الاستقبال. يتم إجراء الاستبدال بواسطة جهاز التشفير ، ويتم التعرف على هذه الكلمات على جانب الاستقبال بواسطة جهاز فك التشفير.

نظرًا لأن دور الأطراف قابل للتغيير ، يتم دمج كلا الجهازين في جهاز واحد يسمى برنامج الترميز المختصر (المشفر / وحدة فك التشفير) ، ويتم تثبيتهما على طرفي القناة. علاوة على ذلك ، نظرًا لوجود كلمات ، فهناك أيضًا أبجدية. الأبجدية مكونة من حرفين {0 ، 1} ، كتلة ثنائيةرموز. أبجدية اللغة الطبيعية (NL) هي مجموعة من الرموز - الحروف التي تحل محل أصوات الكلام الشفهي عند الكتابة. هنا لن نتعمق في الكتابة الهيروغليفية في الكتابة المقطعية أو العقدية.

الأبجدية والكلمات هي بالفعل لغة ، ومن المعروف أن اللغات البشرية الطبيعية زائدة عن الحاجة ، ولكن ما يعنيه هذا ، حيث يصعب القول ، حيث يسكن التكرار اللغوي ، فإن التكرار ليس منظمًا جيدًا وفوضويًا. عند ترميز المعلومات وتخزينها ، فإنها تميل إلى تقليل التكرار ، على سبيل المثال ، المحفوظات ، شفرة مورس ، إلخ

ربما أدرك ريتشارد هيمنج قبل الآخرين أنه إذا لم يتم التخلص من التكرار ، ولكن تم تنظيمه بشكل معقول ، فيمكن استخدامه في أنظمة الاتصال لاكتشاف الأخطاء وتصحيحها تلقائيًا في كلمات التشفير للنص المرسل. لقد أدرك أنه يمكن استخدام 128 كلمة ثنائية مكونة من سبع بتات للكشف عن الأخطاء في كلمات التشفير التي تشكل رمزًا - مجموعة فرعية من 16 كلمة ثنائية من سبع بتات. كان تخمينا رائعا.

قبل اختراع Hamming ، تم اكتشاف الأخطاء أيضًا من قبل الجانب المتلقي عندما لا يمكن قراءة النص الذي تم فك تشفيره أو تبين أنه لم يكن مطلوبًا تمامًا. في هذه الحالة ، تم إرسال طلب إلى مرسل الرسالة لتكرار كتل كلمات معينة ، والتي ، بالطبع ، كانت غير مريحة للغاية وأبطأت جلسات الاتصال. كانت هذه مشكلة كبيرة لم يتم حلها منذ عقود.

بناء (7 ، 4) كود هامينج

دعنا نعود إلى هامينغ. تتكون كلمات الكود (7 ، 4) من 7 بتات j =

(i_{1}, i_{2}, i_{3}, i_{4}, p_{1}, p_{2}, p_{3})

$(i_1,i_2,i_3,i_4,p_1,p_2,p_3)$ ، j = 0 (1) 15، 4-information and 3-check الرموز ، أي في الأساس زائدة عن الحاجة ، لأنها لا تحمل معلومات عن الرسائل. كان من الممكن تمثيل أرقام التحقق الثلاثة هذه بوظائف خطية مكونة من 4 رموز معلومات في كل كلمة ، مما يضمن اكتشاف حقيقة الخطأ ومكانه في الكلمات من أجل إجراء تصحيح. حصل الرمز A (7 ، 4) على صفة جديدة وأصبح كتلة ثنائية خطية .

التبعيات الوظيفية الخطية (القواعد (*)) لحساب قيم الرموز

p_{i}

$p_i$ يبدو مثل هذا:

p_{1} + i_{2} + i_{3} + i_{4} = 0, \to p_{1} = i_{2} + i_{3} + i_{4},

$p_1 + i_2 +i_3 + i_4 = 0, → p_1 = i_2 + i_3 + i_4,$

p_{2} + i_{1} + i_{3} + i_{4} = 0, \to p_{2} = i_{1} + i_{3} + i_{4}, (*)

$p_2 + i_1 + i_3 + i_4 = 0, → p_2 = i_1+ i_3 + i_4, (*)$

p_{3} + i_{1} + i_{2} + i_{4} = 0, \to p_{3} = i_{1} + i_{2} + i_{4} .

$p_3 + i_1 + i_2 + i_4 = 0, → p_3 = i_1+i_2 + i_4.$

أصبح تصحيح الخطأ عملية بسيطة للغاية - تم تحديد حرف (صفر أو واحد) في البت الخاطئ واستبداله بآخر مقابل 0 بمقدار 1 أو 1 في 0.

كم عدد الكلمات المختلفة التي تشكل الكود؟ الجواب على هذا السؤال للرمز (7 ، 4) بسيط للغاية. نظرًا لوجود 4 أرقام معلومات فقط ، فإن تنوعها ، عند ملئه بالرموز ، يحتوي على

2^{4}

$2^4$ = 16 خيارًا ، إذن ببساطة لا توجد احتمالات أخرى ، أي أن الكود الذي يتكون من 16 كلمة فقط يضمن أن هذه الكلمات الـ 16 تمثل الكتابة الكاملة للغة بأكملها.

الأجزاء المعلوماتية لهذه الكلمات الـ 16 مرقمة #

(

i_{1}, i_{2}, i_{3}, i_{4}

$i_1,i_2,i_3,i_4$ ):

0 = 0000 ؛ 4 = 0100 ؛ 8 = 1000 ؛ 12 = 1100 ؛

1 = 0001 ؛ 5 = 0101 ؛ 9 = 1001 ؛ 13 = 1101 ؛

2 = 0010 ؛ 6 = 0110 ؛ 10 = 1010 ؛ 14 = 1110 ؛

3 = 0011 ؛ 7 = 0111 ؛ 11 = 1011 ؛ 15 = 1111.

يجب حساب كل كلمة من هذه الكلمات المكونة من 4 بتات وإضافتها إلى اليمين بمقدار 3 بتات تحقق ، والتي يتم حسابها وفقًا للقواعد (*). على سبيل المثال ، بالنسبة لكلمة المعلومات رقم 6 تساوي 0110 ، لدينا

i_{1} = 0, i_{2} = 1, i_{3} = 1, i_{4} = 0

$i_1=0, i_2=1, i_3=1,i_4=0$ ويعطي تقييم أحرف الشيك النتيجة التالية لهذه الكلمة:

(р_{1} = 0, р_{2} = 1, р_{3} = 1)

$(_1 = 0, _2 = 1, _3 = 1)$

р_{1} = i_{2} + i_{3} + i_{4} = 1 + 1 + 0 (m o d 2) = 2 (m o d 2) = 0,

$_1=i_2 +i_3 +i_4 =1 + 1 + 0(mod2)=2(mod2)=0,$

р_{2} = i_{1} + i_{3} + i_{4} = 0 + 1 + 0 (m o d 2) = 1 (m o d 2) = 1,

$_2=i_1 +i_3 +i_4 =0 + 1 + 0(mod2)=1(mod2)=1,$

р_{3} = i_{1} + i_{2} + i_{4} = 0 + 1 + 0 (m o d 2) = 1 (m o d 2) = 1.

$_3=i_1 +i_2 +i_4 =0 + 1 + 0(mod2)=1(mod2)=1.$

في هذه الحالة ، تأخذ كلمة الشفرة السادسة الشكل:

С_{6} = (i_{1}, i_{2}, i_{3}, i_{4}, p_{1}, p_{2}, p_{3}) = (0110011) .

$_6=(i_1,i_2,i_3,i_4,p_1,p_2,p_3)=(0110011).$ بنفس الطريقة ، من الضروري حساب رموز التحقق لجميع الكلمات المشفرة الستة عشر. دعنا نجهز جدولًا مكونًا من 16 سطرًا لكلمات الشفرة ونملأ خلاياه بالتتابع (أوصي القارئ بعمل ذلك باستخدام قلم رصاص في يده).

الجدول K - كلمات التشفير j ، j = 0 (1) 15 ، (7 ، 4) - رموز هامينج

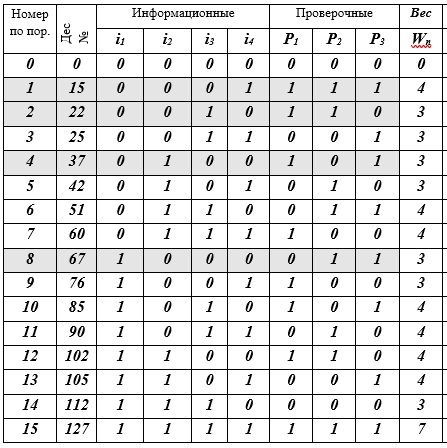
وصف الجدول: 16 سطرًا - كلمات رمزية ؛ 10 أعمدة: رقم التسلسل ، التمثيل العشري لكلمة التشفير ، 4 رموز معلومات ، 3 رموز فحص ، وزن W لكلمة الرمز يساوي عدد البتات غير الصفرية (≠ 0). يتم تمييز 4 خطوط كلمات رمزية عن طريق التعبئة - وهذا هو أساس الفضاء الجزئي المتجه. في الواقع ، هذا كل شيء - تم إنشاء الكود.

وهكذا ، يحتوي الجدول على جميع الكلمات (7 ، 4) - رمز هامينغ. كما ترى ، لم يكن الأمر صعبًا للغاية. بعد ذلك ، سوف نتحدث عن الأفكار التي أدت إلى إنشاء هذا الكود. نحن جميعًا على دراية بشفرة مورس ، مع أبجدية السمافور البحرية والأنظمة الأخرى المبنية على مبادئ إرشادية مختلفة ، ولكن هنا في (7 ، 4) يتم استخدام مبادئ وطرق رياضية صارمة لأول مرة. ستكون القصة عنهم فقط.

الأسس الرياضية للكود. الجبر العالي

حان الوقت لمعرفة كيف جاء R. Hemming بفكرة فتح مثل هذا الرمز. لم يكن لديه أوهام خاصة حول موهبته وصاغ مهمة لنفسه بشكل متواضع: إنشاء رمز يكتشف ويصحح خطأ واحد في كل كلمة (في الواقع ، تم اكتشاف خطأين ، ولكن تم تصحيح خطأ واحد فقط). مع جودة القنوات ، حتى خطأ واحد هو حدث نادر. لذلك ، كانت خطة Hemming لا تزال كبيرة على نطاق نظام الاتصالات. حدثت ثورة في نظرية الترميز بعد نشرها.

كان ذلك عام 1950. أقدم هنا وصفي البسيط (آمل أن يكون مفهومًا) ، والذي لم أره من المؤلفين الآخرين ، ولكن كما اتضح ، كل شيء ليس بهذه البساطة. لقد تطلب الأمر معرفة من العديد من مجالات الرياضيات والوقت لفهم كل شيء بعمق وفهم بنفسك لماذا يتم ذلك بهذه الطريقة. بعد ذلك فقط تمكنت من تقدير الفكرة الجميلة والبسيطة إلى حد ما التي يتم تنفيذها في كود التصحيح هذا. قضيت معظم الوقت في التعامل مع تقنية الحسابات والتبرير النظري لجميع الإجراءات التي أكتب عنها هنا.

لم يستطع منشئو الأكواد ، لفترة طويلة ، التفكير في رمز يكتشف ويصحح خطأين. الأفكار التي استخدمها Hemming لم تنجح هناك. كان علي أن أنظر ، وتم العثور على أفكار جديدة. مثير جدا! يأسر. استغرق الأمر حوالي 10 سنوات للعثور على أفكار جديدة ، وبعد ذلك فقط كان هناك اختراق. تم استلام الرموز التي تظهر عددًا عشوائيًا من الأخطاء بشكل سريع نسبيًا.

مساحات ناقلات وحقول ومجموعات . يمثل الكود الناتج (7 ، 4) (الجدول K) مجموعة من الكلمات المشفرة التي تشكل عناصر فضاء فرعي متجه (من أجل 16 ، مع البعد 4) ، أي جزء من فضاء متجه البعد 7 بالترتيب

2^{7} = 128.

$2^7=128.$ من بين 128 كلمة ، تم تضمين 16 كلمة فقط في الكود ، ولكن تم تضمينها في الكود لسبب ما.

أولاً ، إنها فضاء فرعي به كل الخصائص والمفردات الناتجة ؛ ثانيًا ، الكلمات المشفرة هي مجموعة فرعية من مجموعة كبيرة من الطلبات 128 ، علاوة على ذلك ، مجموعة فرعية مضافة من مجال جالوا الممتد المنتهي GF (

2^{7}

$2^7$ ) درجة التمدد n = 7 والخصائص 2. تتحلل هذه المجموعة الفرعية الكبيرة إلى فئات متجاورة بواسطة مجموعة فرعية أصغر ، وهو موضح جيدًا في الجدول التالي د. ينقسم الجدول إلى جزأين: علوي وسفلي ، لكن يجب قراءته على أنه واحد طويل. كل فئة مجاورة (صف الجدول) هي عنصر من مجموعة العوامل من خلال تكافؤ المكونات.

الجدول د - تحلل المجموعة المضافة لحقل جالوا GF ( $2^7$ ) في مجموعات (صفوف الجدول D) للمجموعة الفرعية ذات الترتيب السادس عشر.

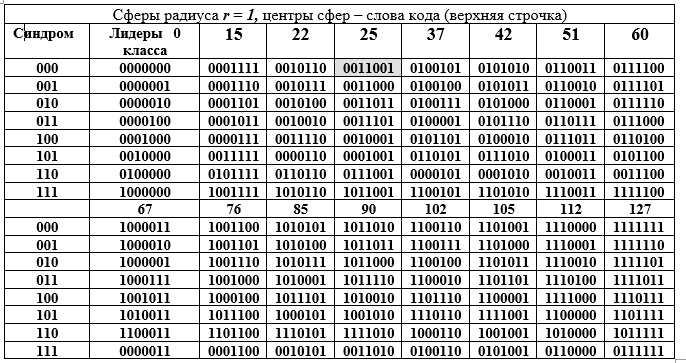
أعمدة الجدول هي مجالات نصف قطرها 1. العمود الأيسر (مكرر) هو متلازمة الكلمة (7 ، 4) رمز هامينج ، العمود التالي هو قادة الطبقة المجاورة. دعنا نفتح التمثيل الثنائي لأحد العناصر (يتم تمييز 25 من خلال ملء) لمجموعة العوامل وتمثيلها العشري:

0 \cdot x^{6} + 0 \cdot x^{5} + 1 \cdot x^{4} + 1 \cdot x^{3} + 0 x^{2} + 0 x + 1 = 1 \cdot 2^{4} + 1 \cdot 2^{3} + 1 \cdot 2^{0} = 16 + 8 + 1 = 25

$0·x^6+0·x^5+1·x^4+1·x^3+0x^2+0x+1=1·2^4+1·2^3+1·2^0=16+8+1=25$

تقنية الحصول على صفوف الجدول D. يتم جمع عنصر من عمود قادة فئة مع كل عنصر من رأس عمود من الجدول D (يتم إجراء التجميع لصف القائد في النموذج الثنائي mod2). نظرًا لأن جميع قادة الفصل لديهم وزن W = 1 ، فإن جميع المجاميع تختلف عن الكلمة الموجودة في عنوان العمود في موضع واحد فقط (نفس الشيء بالنسبة للصف بأكمله ، ولكن يختلف بالنسبة للعمود). يحتوي الجدول D على تفسير هندسي رائع. يتم تمثيل جميع الكلمات المشفرة الستة عشر بمراكز المجالات في الفضاء المتجه ذي الأبعاد السبعة. تختلف كل الكلمات في العمود عن الكلمة العلوية في نفس الموضع ، أي أنها تقع على سطح كرة نصف قطرها r = 1.

يخفي هذا التفسير فكرة اكتشاف خطأ واحد في أي كلمة رمزية. نحن نعمل مع المجالات. الشرط الأول لاكتشاف الخطأ هو أن مجالات نصف القطر 1 لا ينبغي أن تلمس أو تتقاطع. هذا يعني أن مراكز الكرات على مسافة 3 أو أكثر من بعضها البعض. في هذه الحالة ، لا تتقاطع المجالات فحسب ، بل لا تلمس بعضها البعض أيضًا. هذا مطلب لعدم غموض القرار: ما المجال الذي يجب أن يُنسب إلى الكلمة الخاطئة المستلمة على جانب الاستقبال بواسطة وحدة فك التشفير (وليس رمز واحد من 128-16 = 112).

ثانيًا ، يتم توزيع المجموعة الكاملة المكونة من 7 بتات من الكلمات الثنائية المكونة من 128 كلمة بالتساوي على 16 مجالًا. يمكن لوحدة فك الترميز الحصول على كلمة فقط من هذه المجموعة المكونة من 128 كلمة معروفة مع وجود خطأ أو بدونه. ثالثًا ، يمكن أن يتلقى الجانب المتلقي كلمة بدون خطأ أو مع تشويه ، ولكنه ينتمي دائمًا إلى واحدة من المجالات الستة عشر ، والتي يمكن تحديدها بسهولة بواسطة وحدة فك التشفير. في الحالة الأخيرة ، يتم اتخاذ قرار بإرسال كلمة مشفرة - مركز الكرة الذي يحدده وحدة فك التشفير ، والذي وجد موضع الكلمة (تقاطع صف وعمود) في الجدول D ، أي رقم العمود والصفوف.

هنا ينشأ مطلب لكلمات الكود وللشفرة ككل: يجب أن تكون المسافة بين أي كلمتين مشفرتين على الأقل ثلاثة ، أي الاختلاف في زوج من كلمات الكود ، على سبيل المثال ، i = 85 =

(i_{1}, i_{2}, i_{3}, i_{4}, p_{1}, p_{2}, p_{3})

$(i_1,i_2,i_3,i_4,p_1,p_2,p_3)$ = 1010101 ؛ j = 25 =

(i_{1}, i_{2}, i_{3}, i_{4}, p_{1}, p_{2}, p_{3})

$(i_1,i_2,i_3,i_4,p_1,p_2,p_3)$ = 0011001 يجب أن يكون على الأقل 3 ؛ 85-25 = 1010101 - 0011001 = 1001100 = 76 ، وزن الفرق كلمة W (76) = 3 (الجدول D يحل محل حساب الفروق والمجموع). هنا ، تُفهم المسافة بين متجهات الكلمات الثنائية على أنها عدد المواضع غير المطابقة في كلمتين. هذه هي مسافة هامينغ ، التي أصبحت مستخدمة على نطاق واسع من الناحية النظرية والعملية ، لأنها تلبي جميع بديهيات المسافة.

ملاحظة . الكود (7 ، 4) ليس فقط رمزًا ثنائيًا للكتلة الخطية ، ولكنه أيضًا رمز مجموعة ، أي أن كلمات الكود تشكل مجموعة جبرية عن طريق الإضافة. هذا يعني أن أي كلمتي تشفير ، عند إضافتهما معًا ، تعطي مرة أخرى إحدى كلمات التشفير. فقط هذه ليست عملية إضافة عادية ، إنها طريقة الإضافة الثانية.

الجدول هـ - مجموع عناصر المجموعة (كلمات مشفرة) المستخدمة لبناء كود هامنج

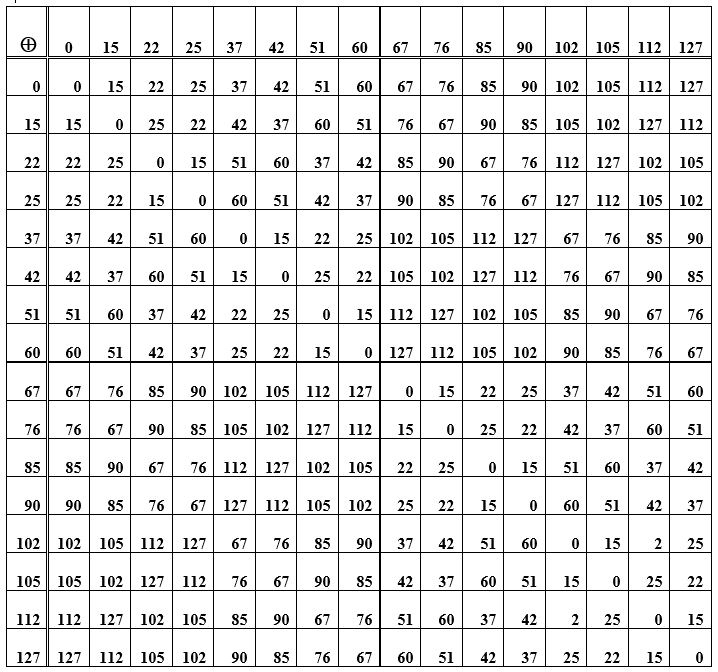
إن عملية جمع الكلمات نفسها هي عملية ترابطية ، ولكل عنصر في مجموعة الكلمات المشفرة هناك نقيض لها ، أي أن جمع الكلمة الأصلية بالعكس يعطي قيمة صفرية. كلمة الكود الصفرية هذه هي العنصر المحايد في المجموعة. في الجدول D ، هذا هو القطر الرئيسي للأصفار. باقي الخلايا (تقاطعات الصف / العمود) عبارة عن تمثيلات رقمية عشرية لكلمات التعليمات البرمجية التي تم الحصول عليها من خلال جمع عناصر من صف وعمود. عند إعادة ترتيب الكلمات في الأماكن (عند الجمع) ، تظل النتيجة كما هي ؛ علاوة على ذلك ، يكون للطرح وإضافة الكلمات نفس النتيجة. علاوة على ذلك ، يتم النظر في نظام التشفير / فك التشفير الذي يطبق مبدأ المتلازمة.

تطبيق الكود. المبرمج

يوجد المشفر على جانب الإرسال للقناة ويستخدمه مرسل الرسالة. يقوم مرسل الرسالة (المؤلف) بتشكيل الرسالة بأبجدية اللغة الطبيعية ويقدمها في شكل رقمي. (اسم الحرف في كود ASCII وفي ثنائي).

من الملائم إنشاء نصوص في ملفات لجهاز كمبيوتر باستخدام لوحة مفاتيح قياسية (رموز ASCII). كل حرف (حرف الأبجدية) في هذا الترميز يتوافق مع ثماني بتات (ثمانية بتات). بالنسبة إلى (7 ، 4) - كود هامينج ، بكلماته يوجد فقط 4 رموز معلومات ، عند ترميز رمز لوحة المفاتيح في حرف ، يلزم وجود كلمتين رمزيتين ، أي يتم تقسيم ثماني بتات من حرف إلى كلمتين معلومات من اللغة الطبيعية (NL) للنموذج

i < 4 >=< i_{1}, i_{2}, i_{3}, i_{4} >

$i<4> = <i_1, i_2, i_3, i_4>$ ...

مثال 1 . من الضروري نقل كلمة "رقم" إلى NL. ندخل جدول رموز ASCII ، وتتوافق الأحرف مع: c –11110110 ، و –11101000 ، و f - 11110100 ، و p - 11110000 ، و - 11100000 ثماني بتات. أو بخلاف ذلك ، في رموز ASCII ، كلمة "digit" = 1111 0110 1110 1000 1111 0100 1111 0000 1110 0000

مع تقسيم إلى رباعي (4 أرقام لكل منها). وبالتالي ، فإن تشفير كلمة "رقم" NL يتطلب 10 كلمات رمزية من (7 ، 4) كود هامينج. تمثل tetrads الأجزاء المعلوماتية لكلمات الرسالة. يتم تحويل كلمات المعلومات هذه (tetrads) إلى كلمات رمزية (7 بت لكل منها) قبل إرسالها إلى قناة شبكة الاتصال. يتم ذلك عن طريق ضرب المصفوفة المتجهة: كلمة المعلومات بواسطة المصفوفة المولدة. الدفع مقابل الراحة مكلف للغاية ويستغرق وقتًا طويلاً ، لكن كل شيء يعمل تلقائيًا والأهم من ذلك ، أن الرسالة محمية من الأخطاء.

يتم الحصول على مصفوفة توليد كود هامينج (7 ، 4) أو مولد كلمة الكود من خلال كتابة المتجهات الأساسية للشفرة ودمجها في مصفوفة. يتبع هذا من نظرية الجبر الخطي: أي متجه لمساحة (فضاء جزئي) هو مزيج خطي من متجهات الأساس ، أي مستقل خطيًا في هذا الفضاء. هذا هو بالضبط ما هو مطلوب - لتوليد أي ناقلات (كلمات كود 7 بت) من المعلومات 4 بت.

مصفوفة توليد (7 ، 4 ، 3) كود هامينج أو مولد كلمة الكود لها الشكل:

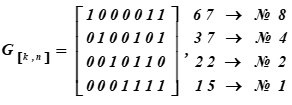
على اليمين توجد التمثيلات العشرية للكلمات المشفرة لأساس الفضاء الجزئي وأرقامها الترتيبية في الجدول K

رقم. i الصفوف من المصفوفة هي كلمات الكود التي تشكل أساس الفضاء الجزئي المتجه.

مثال على كلمات ترميز رسائل المعلومات (تم إنشاء مصفوفة توليد الكود من متجهات الأساس وتتوافق مع جزء الجدول K). في جدول رموز ASCII ، نأخذ الحرف q = <1111 0110>.

تبدو كلمات المعلومات للرسالة كما يلي:

i_{k 1} =< 1111 >, i_{k 2} =< 0110 >

$i_{k1} = <1111>, i_{k2} = <0110>$ ...

هذه نصف الحرف (ج). بالنسبة للرمز (7 ، 4) المحدد سابقًا ، يلزم العثور على كلمات الشفرة المقابلة لكلمة رسالة المعلومات (ج) المكونة من 8 أحرف في النموذج:

i_{k 1} =< 1111 >, i_{k 2} =< 0110 >

$i_{k1} = <1111>, i_{k2} = <0110>$ ...

لتحويل هذه الرسالة-الرسالة (q) إلى كلمات مشفرة u ، يتم ضرب كل نصف رسالة الحرف i بمصفوفة التوليد G [k، n] من الكود (مصفوفة للجدول K):

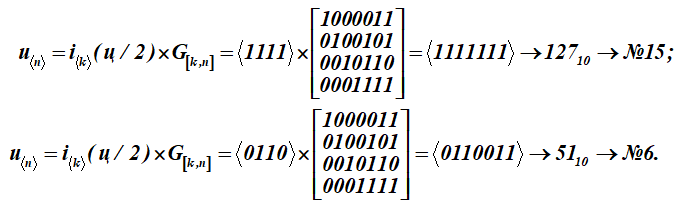
حصلنا على كلمتين مشفرتين برقمين تسلسليين 15 و 6.

إظهار تشكيل مفصل للنتيجة السفلية رقم 6 - كلمة مشفرة (ضرب صف كلمة المعلومات بأعمدة مصفوفة التوليد) ؛ الجمع فوق (نموذج 2)

<0110> ∙ <1000> = 0 1 + 1 ∙ 0 + 1 ∙ 0 + 0 0 = 0 (نموذج 2) ؛

<0110> ∙ <0100> = 0 0 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 0 = 1 (نموذج 2) ؛

<0110> ∙ <0010> = 0 0 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 0 = 1 (نموذج 2) ؛

<0110> ∙ <0001> = 0 0 + 1 ∙ 0 + 1 0 + 0 ∙ 1 = 0 (نموذج 2) ؛

<0110> ∙ <0111> = 0 0 + 1 ∙ 1 + 1 ∙ 1 + 0 ∙ 1 = 0 (نموذج 2) ؛

<0110> ∙ <1011>= 0 ∙ 1 + 1 ∙ 0 + 1 ∙ 1 + 0 ∙ 1 = 1 (نموذج 2) ؛

<0110> ∙ <1101> = 0 1 + 1 ∙ 1 + 1 ∙ 0 + 0 ∙ 1 = 1 (نموذج 2).

تم تلقي الكلمات الخامسة عشرة والسادسة من الجدول K. نتيجة الضرب ، وتمثل البتات الأربع الأولى في كلمات الشفرة هذه (نتائج الضرب) كلمات المعلومات. تبدو مثل:

i_{k 1} =< 1111 >, i_{k 2} =< 0110 >

$i_{k1} = <1111>, i_{k2}= <0110>$ ، (في جدول ASCII نصف الحرف t فقط). بالنسبة لمصفوفة التشفير ، يتم تحديد مجموعة الكلمات ذات الأرقام: 1 ، 2 ، 4 ، 8 كمتجهات أساسية في الجدول K. في الجدول يتم تمييزها عن طريق التعبئة. ثم بالنسبة لهذا الجدول K ، ستتلقى مصفوفة التشفير الصيغة G [k، n].

نتيجة الضرب ، تم الحصول على 15 و 6 كلمات من جدول الكود K.

تطبيق الكود. فك

يوجد مفكك التشفير على جانب الاستقبال للقناة حيث يوجد مستقبل الرسالة. الغرض من وحدة فك التشفير هو تزويد المستلم بالرسالة المرسلة بالشكل الذي كانت موجودة به لدى المرسل وقت الإرسال ، أي يمكن للمستلم استخدام النص واستخدام المعلومات منه لعمل إضافي.

تتمثل المهمة الرئيسية لوحدة فك التشفير في التحقق مما إذا كانت الكلمة المستلمة (7 بتات) هي الكلمة التي تم إرسالها على جانب الإرسال ، وما إذا كانت الكلمة تحتوي على أخطاء. لحل هذه المشكلة ، لكل كلمة يستقبلها مفكك الشفرة ، بضربها في مصفوفة الفحص H [nk، n] ، يتم حساب متلازمة المتجه القصيرة S (3 بتات).

بالنسبة للكلمات التي تكون رمزًا ، أي لا تحتوي على أخطاء ، تأخذ المتلازمة دائمًا قيمة صفرية S = <000>. بالنسبة للكلمة التي بها خطأ ، فإن المتلازمة ليست صفرية S ≠ 0. إن قيمة المتلازمة تجعل من الممكن الكشف عن موضع الخطأ وتحديد موقعه حتى قليلاً في الكلمة المستلمة على جانب الاستقبال ، ويمكن لوحدة فك التشفير تغيير قيمة هذا البت. في مصفوفة التحقق من الكود ، يجد مفكك الشفرة عمودًا يتزامن مع قيمة المتلازمة ، ويكون الرقم الترتيبي لهذا العمود مساويًا للبت التالف بسبب الخطأ. بعد ذلك ، بالنسبة للرموز الثنائية ، يقوم مفكك الشفرة بتغيير هذا البت - ببساطة استبدلها بالقيمة المعاكسة ، أي ، يتم استبدال واحد بصفر ، ويتم استبدال الصفر بواحد.

الكود المعني منظم، أي ، يتم وضع رموز كلمة المعلومات في صف في أهم أجزاء كلمة الشفرة. يتم إجراء استعادة كلمات المعلومات عن طريق التخلص البسيط من البتات (التحقق) الأقل أهمية ، والتي يُعرف عددها. علاوة على ذلك ، يتم استخدام جدول رموز ASCII بترتيب عكسي: المدخلات عبارة عن تسلسلات ثنائية إعلامية ، والمخرج هو أحرف الأبجدية للغة الطبيعية. إذن ، (7 ، 4) - كود نظامي ، جماعي ، خطي ، كتلة ، ثنائي .

يتكون أساس مفكك الشفرة من مصفوفة التحقق [nk، n] ، والتي تحتوي على عدد الصفوف المساوية لعدد رموز التحقق ، وجميع الأعمدة الممكنة ، باستثناء الصفر ، أعمدة من ثلاثة أحرف

2^{3} - 1 = 7

$2^3 – 1 = 7$ ... يتم إنشاء مصفوفة التحقق من التكافؤ من كلمات الجدول K ، ويتم اختيارها بحيث تكون متعامدة مع مصفوفة التشفير ، أي حاصل ضربهم هو المصفوفة الصفرية. تأخذ مصفوفة الشيك الشكل التالي في عمليات الضرب ، يتم تبديلها. للحصول على مثال محدد ، مصفوفة التحقق H [nk، n] معطاة أدناه:

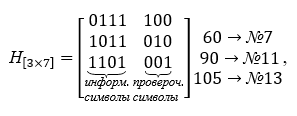
نرى أن حاصل ضرب مصفوفة التوليد ومصفوفة الفحص ينتج عنه مصفوفة صفرية.

مثال 2. فك شفرة كلمة هامنج بدون أخطاء (e <7> = <0000000>).

اسمح في الطرف المستقبل لكلمات القناة # 7 → 60 و # 13 → 105 من الجدول K ،

u <7> + e <7> = <0 1 1 1 1 0 0> + <0 0 0 0 0 0 0> ،

حيث لا يوجد خطأ ، أي يكون على شكل e <7> = <0 0 0 0 0 0 0>.

ونتيجة لذلك ، فإن المتلازمة المحسوبة لها قيمة صفرية ، مما يؤكد عدم وجود خطأ في كلمات الكود.

مثال 3 . الكشف عن خطأ واحد في كلمة تم استقبالها عند الطرف المستقبل للقناة (الجدول K).

أ) دع الأمر مطلوبًا لإرسال كلمة المرور السابعة ، أي

u <7> = <0 1 1 1 1 0 0> وفي الثلث الأيسر من الكلمة حدث خطأ. ثم يتم جمعها mod2 مع الكلمة الكود السابعة المنقولة عبر قناة الاتصال

u <7> + <7> = <0 1 1 1 1 0 0> + <0 0 1 0 0 0 0> = <0 1 0 1 1 0 0> ،

حيث يكون للخطأ شكل e <7> = <0 0 1 0 0 0 0>.

يتم إجراء إثبات حقيقة تشويه كلمة الشفرة بضرب الكلمة المشوهة المستلمة في مصفوفة التحقق من الكود. ستكون نتيجة هذا الضرب متجهًاتسمى متلازمة كلمة السر.

لنقم بمثل هذا الضرب لبياناتنا الأصلية (المتجه السابع مع وجود خطأ).

نتيجة لمثل هذا الضرب ، في الطرف المتلقي للقناة ، تم الحصول على متلازمة ناقل S <nk> ، أبعادها (n - k). إذا كانت المتلازمة S <3> = <0،0،0> تساوي صفرًا ، فيُستنتج أن الكلمة المستلمة على الجانب المتلقي تنتمي إلى رمز C ويتم نقلها دون تشويه. إذا كانت المتلازمة لا تساوي صفر S <3> ≠ <0،0،0> ، فإن قيمتها تشير إلى وجود خطأ ومكانه في الكلمة. تتوافق البتة المشوهة مع رقم موضع عمود المصفوفة [nk، n] ، والذي يتطابق مع المتلازمة. بعد ذلك ، يتم تصحيح البتة المشوهة ، وتتم معالجة الكلمة المستلمة بواسطة وحدة فك التشفير بشكل أكبر. في الممارسة العملية ، يتم حساب متلازمة على الفور لكل كلمة مقبولة ، وإذا كان هناك خطأ ، يتم التخلص منه تلقائيًا.

لذلك ، أثناء الحسابات ، المتلازمة S = <110> هي نفسها لكلتا الكلمتين. ننظر إلى مصفوفة الشيك ونجد عمودًا فيها يطابق المتلازمة. هذا هو العمود الثالث من اليسار. لذلك حدث الخطأ في الخانة الثالثة من اليسار والتي تتطابق مع شروط المثال. يتم تغيير هذه البتة الثالثة إلى القيمة المعاكسة وقمنا بإرجاع الكلمات التي تلقتها وحدة فك التشفير إلى نموذج الكود. تم العثور على الخطأ وإصلاحه.

هذا كل شيء ، هذه هي الطريقة التي يعمل ويعمل بها كود هامينج الكلاسيكي (7 ، 4).

لا يتم النظر هنا في العديد من التعديلات والترقيات لهذا الرمز ، حيث إنها ليست مهمة ، ولكن تلك الأفكار وتطبيقاتها هي التي غيرت بشكل جذري نظرية الترميز ، ونتيجة لذلك ، نظم الاتصال ، وتبادل المعلومات ، وأنظمة التحكم الآلي.

خاتمة

تتناول الورقة الأحكام والمهام الرئيسية لأمن المعلومات ، وتسمية النظريات المصممة لحل هذه المشكلات.

تنتمي مهمة حماية تفاعل المعلومات بين الموضوعات والأشياء من الأخطاء البيئية ومن أفعال المتسلل إلى علم الشفرات.

يتم النظر في كود هامينج (7 ، 4) بالتفصيل ، والذي وضع الأساس لاتجاه جديد في نظرية الترميز - توليف رموز التصحيح.

يتم عرض تطبيق الأساليب الرياضية الصارمة المستخدمة في تركيب الكود.

يتم إعطاء أمثلة لتوضيح كفاءة الكود.

الأدب

بيترسون دبليو ، ويلدون إي. أكواد تصحيح الخطأ: Trans. من الانجليزية. م: مير ، 1976 ، 594 ص.

Bleihut R. نظرية وممارسة أكواد التحكم في الخطأ. مترجم من اللغة الإنجليزية. م: مير ، 1986 ، 576 ص.

رموز التصحيح. بداية نظرية ترميز جديدة