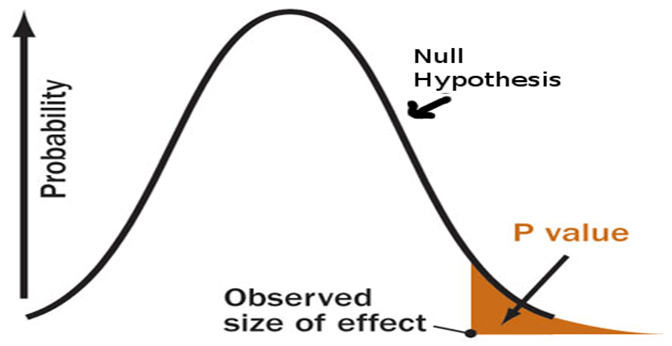
في ذلك الوقت ، لم أكن أعرف أي شيء عن القيمة الاحتمالية أو اختبار الفرضيات أو حتى الدلالة الإحصائية.
قررت استخدام كلمة "p-value" على google ، وما وجدته على ويكيبيديا جعلني أكثر إرباكًا ...
عند اختبار الفرضيات الإحصائية ، فإن القيمة الاحتمالية أو القيمة الاحتمالية لنموذج إحصائي معين هي الاحتمال ، إذا كانت الفرضية الصفرية صحيحة ، فإن الملخص الإحصائي (على سبيل المثال ، القيمة المطلقة لفرق متوسط العينة بين مجموعتين مقارنتين) سيكون أكبر من أو يساوي النتائج الفعلية الملاحظة.عمل جيد ، ويكيبيديا.
- ويكيبيديا
حسنا. لم أفهم ما تعنيه القيمة الاحتمالية في الواقع.
عندما تعمقت في مجال علم البيانات ، بدأت أخيرًا في فهم معنى القيمة p وأين يمكن استخدامها كجزء من أدوات صنع القرار في تجارب معينة.
لذلك قررت أن أشرح قيمة p في هذه المقالة ، وكذلك كيف يمكن استخدامها في اختبار الفرضيات ، لمنحك فهمًا أفضل وأكثر سهولة للقيم p.
كما لا يمكننا تفويت الفهم الأساسي للمفاهيم الأخرى وتعريف القيمة الاحتمالية ، وأعد بأنني سأجعل هذا التفسير بديهيًا دون تعريضك لجميع المصطلحات الفنية التي صادفتها.
هناك أربعة أقسام في هذه المقالة لإعطائك صورة كاملة من بناء اختبار فرضية لفهم القيمة p واستخدامها في عملية اتخاذ القرار. أوصي بشدة بالاطلاع على كل منهم للحصول على فهم مفصل لقيم p:
- اختبار الفرضيات
- التوزيع الطبيعي
- ما هي القيمة الاحتمالية؟
- دلالة إحصائية
سيكون ممتعا.
لنبدأ!
1. اختبار الفرضيات
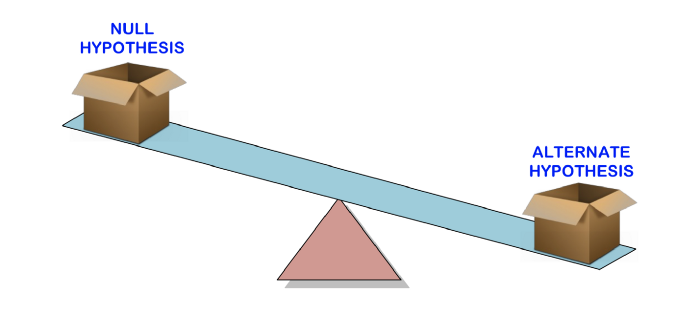
قبل أن نتحدث عن ما تعنيه القيمة p ، فلنبدأ بالنظر في اختبار الفرضيات ، حيث يتم استخدام القيمة p لتحديد الأهمية الإحصائية لنتائجنا.
هدفنا النهائي هو تحديد الأهمية الإحصائية لنتائجنا.
والدلالة الإحصائية مبنية على هذه الأفكار الثلاثة البسيطة:
- اختبار الفرضيات
- التوزيع الطبيعي
- ف القيمة
يستخدم اختبار الفرضية لاختبار صحة بيان (فرضية فارغة) تم إجراؤه حول مجموعة سكانية باستخدام بيانات العينة. الفرضية البديلة هي التي كنت ستصدقها إذا تبين أن الفرضية الصفرية خاطئة.
بمعنى آخر ، سننشئ مطالبة (فرضية فارغة) ونستخدم بيانات العينة للتحقق مما إذا كانت المطالبة صحيحة. إذا كانت العبارة غير صحيحة ، فسنختار فرضية بديلة. كل شيء بسيط للغاية.
لمعرفة ما إذا كانت المطالبة صحيحة أم لا ، سوف نستخدم القيمة الاحتمالية لتقييم قوة الدليل لمعرفة ما إذا كانت ذات دلالة إحصائية. إذا كان الدليل يدعم الفرضية البديلة ، فإننا نرفض الفرضية الصفرية ونقبل الفرضية البديلة. سيتم شرح ذلك في القسم التالي.
دعنا نستخدم مثالاً لجعل هذا المفهوم أكثر وضوحًا ، وسيتم استخدام هذا المثال في هذه المقالة لمفاهيم أخرى.
مثال. لنفترض أن مطعم بيتزا يدعي أن متوسط وقت التوصيل يبلغ 30 دقيقة أو أقل ، لكنك تعتقد أنه أطول مما هو مذكور. لذلك عليك إجراء اختبار فرضية واختيار وقت التسليم بشكل عشوائي لاختبار الإدعاء:
- — 30
- — 30
- , , — — , .
سنستخدم اختبارًا أحادي الاتجاه في حالتنا ، حيث إنه من المهم فقط بالنسبة لنا أن يتجاوز متوسط وقت التسليم 30 دقيقة. لن نفكر في هذا الاحتمال في الاتجاه الآخر ، حيث إن نتائج متوسط وقت التسليم أقل من أو يساوي 30 دقيقة هي الأفضل. هنا نريد التحقق مما إذا كان هناك احتمال أن يكون متوسط وقت التسليم أكثر من 30 دقيقة. بعبارة أخرى ، نريد أن نرى ما إذا كان مطعم البيتزا قد خدعنا.
إحدى الطرق الشائعة لاختبار الفرضيات هي استخدام اختبار Z. لن نخوض في التفاصيل هنا ، لأننا نريد أن نفهم بشكل أفضل ما يحدث على السطح قبل الغوص بشكل أعمق.
2. التوزيع الطبيعي
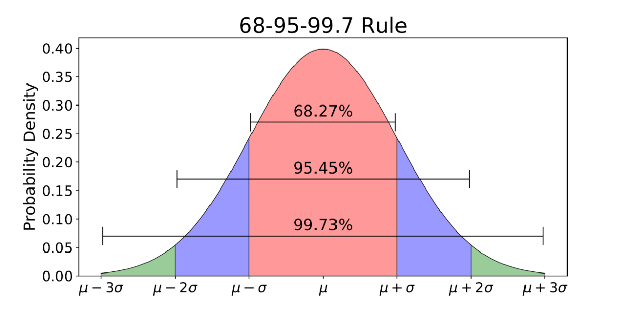
التوزيع الطبيعي هو دالة كثافة احتمالية تستخدم لعرض توزيع البيانات.
التوزيع الطبيعي له معلمتان ، المتوسط (μ) والانحراف المعياري ، ويسمى أيضًا سيجما (σ).
المتوسط هو الاتجاه المركزي في التوزيع. يحدد موقع الذروة للتوزيعات العادية. الانحراف المعياري هو مقياس للتغير. إنه يحدد إلى أي مدى تميل القيم إلى الانخفاض.
عادةً ما يرتبط التوزيع الطبيعي بقاعدة 68-95-99.7 (الصورة أعلاه).
- 68٪ من البيانات ضمن انحراف معياري واحد (σ) من المتوسط (μ)
- 95٪ من البيانات ضمن انحرافين معياريين () من المتوسط (μ)
- 99.7٪ من البيانات ضمن 3 انحرافات معيارية (σ) من المتوسط (μ)
هل تتذكر عتبة الخمس سيجما لبوزون هيغز التي تحدثت عنها في البداية؟ 5 سيجما هي حوالي 99.99999426696856٪ من البيانات التي يجب الحصول عليها قبل أن يؤكد العلماء اكتشاف بوزون هيغز. كان هذا حدًا صارمًا تم تعيينه لتجنب أي إشارات خاطئة محتملة.
رائع. الآن ، قد تتساءل ، "كيف يرتبط التوزيع الطبيعي باختبار فرضيتنا السابق؟"
نظرًا لأننا استخدمنا اختبار Z لاختبار فرضيتنا ، فنحن بحاجة إلى حساب درجات Z (التي سيتم استخدامها في إحصائيات الاختبار الخاصة بنا) ، وهي عدد الانحرافات المعيارية عن متوسط نقطة البيانات. في حالتنا ، كل نقطة بيانات هي وقت توصيل البيتزا الذي تلقيناه. لاحظ أنه عندما حسبنا جميع درجات Z لكل وقت تسليم بيتزا ورسمنا منحنى توزيع عادي قياسي كما هو موضح أدناه ، ستتغير الوحدة الموجودة على المحور X من الدقائق إلى وحدة الانحراف المعياري حيث قمنا بتوحيد المتغير بطرح المتوسط والقسمة عن طريق الانحراف المعياري (انظر الصيغة أعلاه). يعد فحص منحنى الجرس القياسي مفيدًا لأنه يمكننا مقارنة نتائج الاختبار بمجموعة "طبيعية" بوحدة معيارية في الانحراف المعياري ، خاصةً عندما يكون لدينا متغير يأتي بوحدات مختلفة.

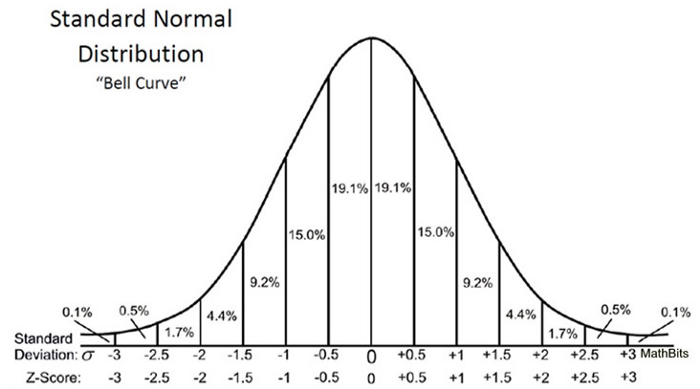
يمكن أن تخبرنا Z-Score بمكان تكمن البيانات الإجمالية مقارنةً بمتوسط عدد السكان.
تعجبني الطريقة التي عبر بها ويل كورسن : كلما كانت درجة Z أعلى أو أقل ، قل احتمال ظهور نتيجة عشوائية وزادت احتمالية أن تكون النتيجة ذات مغزى.
ولكن ما مدى ارتفاع (أو انخفاض) المقنع بما يكفي لتحديد مدى أهمية نتائجنا؟
ذروة
هنا ، نحتاج إلى القطعة الأخيرة لحل اللغز ، والقيمة p ، ومعرفة ما إذا كانت نتائجنا ذات دلالة إحصائية بناءً على مستوى الأهمية (المعروف أيضًا باسم alpha) الذي حددناه قبل بدء تجربتنا.
3. ما هي القيمة الاحتمالية؟
أخيرًا ... نحن نتحدث هنا عن قيمة p!
تهدف جميع التفسيرات السابقة إلى تمهيد الطريق وقيادتنا إلى هذه القيمة الاحتمالية. نحتاج إلى السياق والخطوات السابقة لفهم هذه القيمة الغامضة (في الواقع ليست غامضة جدًا) وكيف يمكن أن تؤدي إلى قراراتنا لاختبار الفرضية.
إذا وصلت إلى هذا الحد ، فاستمر في القراءة. لأن هذا القسم هو الجزء الأكثر إثارة منهم جميعًا!
بدلاً من شرح قيم p باستخدام التعريف الذي قدمته Wikipedia (آسف Wikipedia) ، دعنا نشرح ذلك في سياقنا - وقت توصيل البيتزا!
للتذكير ، اخترنا عشوائيًا بعض أوقات توصيل البيتزا ، والهدف هو التحقق مما إذا كان وقت التسليم يتجاوز 30 دقيقة. إذا كان الدليل النهائي يدعم مطالبة مطعم البيتزا (متوسط وقت التسليم 30 دقيقة أو أقل) ، فلن نرفض فرضية العدم. خلاف ذلك ، فإننا ندحض فرضية العدم.
لذا فإن مهمة p-value هي الإجابة على هذا السؤال:
إذا كنت أعيش في عالم تكون فيه أوقات توصيل البيتزا 30 دقيقة أو أقل (الفرضية الصفرية صحيحة) ، فما مدى توقعي في الواقع؟تجيب القيمة P على هذا السؤال برقم - احتمال.
كلما انخفضت قيمة p ، كلما كان الدليل غير متوقع ، وكلما كانت فرضية العدم تبدو سخيفة.
وماذا نفعل عندما نشعر بالسخرية من فرضيتنا الصفرية؟ نحن نرفضه ونختار فرضيتنا البديلة.
إذا كانت القيمة p أقل من مستوى أهمية معين (يسميها الناس ألفا ، أسمي هذا عتبة السخافة - لا تسأل لماذا ، من الأسهل بالنسبة لي فهمها) ، فإننا نرفض فرضية العدم.
الآن نحن نفهم ما تعنيه القيمة p. دعونا نطبق هذا في حالتنا.
قيمة P في حساب وقت توصيل البيتزا
الآن بعد أن قمنا بجمع بعض بيانات العينة عن أوقات التسليم ، أجرينا الحساب ووجدنا أن متوسط وقت التسليم كان أطول بـ 10 دقائق بقيمة p 0.03.
هذا يعني أنه في عالم تكون فيه أوقات توصيل البيتزا 30 دقيقة أو أقل (الفرضية الصفرية صحيحة) ، هناك احتمال بنسبة 3٪ أننا سنرى متوسط وقت توصيل أطول بـ 10 دقائق على الأقل بسبب الضوضاء العشوائية. ...
كلما كانت القيمة الاحتمالية أصغر ، كانت النتيجة ذات مغزى أكبر ، لأنه من غير المرجح أن تكون ناتجة عن الضوضاء.
في حالتنا ، يسيء معظم الناس فهم القيمة الاحتمالية:
تعني القيمة الاحتمالية البالغة 0.03 وجود 3٪ (احتمال النسبة المئوية) أن النتيجة ناتجة عن الصدفة - وهذا ليس صحيحًا.غالبًا ما يريد الناس إجابة محددة (بما في ذلك أنا) ، ولهذا السبب كنت مرتبكًا لفترة طويلة مع تفسير قيم p.
لا تثبت القيمة الاحتمالية أي شيء. إنها مجرد طريقة لاستخدام المفاجأة كأساس لقرار ذكي.إليك كيف يمكننا استخدام القيمة الاحتمالية 0.03 لمساعدتنا في اتخاذ قرارات ذكية (مهم):
- كاسي كوزيركوف
- تخيل أننا نعيش في عالم حيث يكون متوسط وقت التوصيل دائمًا 30 دقيقة أو أقل - لأننا نؤمن بمطعم البيتزا (إيماننا الأصلي)!
- بعد تحليل وقت تسليم العينات التي تم جمعها ، تكون القيمة p أقل بـ 0.03 من مستوى الأهمية 0.05 (بافتراض أننا حددنا هذه القيمة قبل تجربتنا) ، ويمكننا القول أن النتيجة ذات دلالة إحصائية.
- , 30 , , , , .
- ? ( ) . , , , , , , .
- , — .
الآن ، ربما تكون قد اكتشفت شيئًا بالفعل ... اعتمادًا على سياقنا ، لا تُستخدم قيم p لإثبات أو تبرير أي شيء.
في رأيي ، يتم استخدام قيم p كأداة لتحدي اعتقادنا الأولي (فرضية العدم) عندما تكون النتيجة ذات دلالة إحصائية. في اللحظة التي نشعر فيها بالسخرية مع إيماننا (بافتراض أن القيمة p تشير إلى أن النتيجة ذات دلالة إحصائية) ، فإننا نتجاهل معتقدنا الأصلي (نرفض فرضية العدم) ونتخذ قرارًا ذكيًا.
4. دلالة إحصائية
أخيرًا ، هذه هي المرحلة الأخيرة حيث نجمع كل شيء معًا ونتحقق مما إذا كانت النتيجة ذات دلالة إحصائية.
لا يكفي أن يكون لديك قيمة p فقط ، فنحن بحاجة إلى تعيين حد (مستوى الأهمية - ألفا). يجب دائمًا تعيين ألفا قبل التجربة لتجنب التحيز. إذا كانت قيمة p الملاحظة أقل من alpha ، فإننا نستنتج أن النتيجة ذات دلالة إحصائية.
القاعدة الأساسية هي ضبط alpha على 0.05 أو 0.01 (مرة أخرى ، تعتمد القيمة على مهمتك).
كما ذكرنا سابقًا ، لنفترض أننا قمنا بتعيين alpha على 0.05 قبل أن نبدأ التجربة ، فإن النتيجة ذات دلالة إحصائية لأن القيمة p البالغة 0.03 أقل من alpha.
كمرجع ، فيما يلي الخطوات الرئيسية للتجربة بأكملها:
- صياغة الفرضية الصفرية
- كوِّن فرضية بديلة
- حدد قيمة ألفا لاستخدامها
- ابحث عن درجة Z المرتبطة بمستوى ألفا الخاص بك
- ابحث عن إحصائيات الاختبار باستخدام هذه الصيغة
- إذا كانت إحصائية الاختبار أقل من درجة ألفا Z (أو كانت القيمة p أقل من قيمة ألفا) ، فقم برفض فرضية العدم. خلاف ذلك ، لا ترفض فرضية العدم.
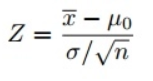
إذا كنت ترغب في معرفة المزيد عن الدلالة الإحصائية ، فلا تتردد في مراجعة هذه المقالة - شرح الدلالة الإحصائية ، بقلم ويل كيرسن .
تأملات لاحقة
هناك الكثير لنستوعبه هنا ، أليس كذلك؟
لا يمكنني إنكار أن قيم p مربكة بطبيعتها لكثير من الناس ، واستغرق الأمر بعض الوقت لفهم وتقدير قيم p وكيف يمكن تطبيقها في عملية اتخاذ القرار لدينا كعلماء بيانات.
لكن لا تعتمد كثيرًا على القيم الاحتمالية ، لأنها تساعد فقط في جزء صغير من عملية صنع القرار بأكملها.
آمل أن يكون توضيحي للقيم p بديهيًا ومفيدًا في فهمك لما تعنيه قيم p حقًا وكيف يمكن استخدامها في اختبار فرضياتك.
حساب قيم p بسيط في حد ذاته. يأتي الجزء الصعب عندما نريد تفسير قيم p في اختبار الفرضيات. نأمل أن يصبح الجزء الصعب الآن أسهل قليلاً بالنسبة لك.
إذا كنت ترغب في معرفة المزيد عن الإحصاء ، فإنني أوصي بشدة بقراءة هذا الكتاب (الذي أقرأه حاليًا!) - إحصاءات عملية لعلماء البيانات ، وهي مكتوبة خصيصًا لعلماء البيانات لفهم المفاهيم الأساسية للإحصاء.

تعرف على المزيد حول كيفية الحصول على مهنة رفيعة المستوى من الصفر أو Level Up في المهارات والراتب من خلال أخذ دورات SkillFactory المدفوعة عبر الإنترنت:
- تدريب مهنة علم البيانات من الصفر (12 شهرًا)
- مهنة المحلل بأي مستوى ابتدائي (9 أشهر)
- Machine Learning (12 )
- «Python -» (9 )
- DevOps (12 )
- - (8 )