قررت التحقق من مفارقة عيد الميلاد باستخدام البيانات المتاحة من VK.
ما هي مفارقة عيد الميلاد؟
حاول الإجابة على السؤال: كم عدد الأشخاص في الغرفة اللازمة لشخصين ليحصلوا على نفس عيد الميلاد مع احتمال 0.5؟ (التاريخ والشهر). مفارقة عيد الميلاد تجيب على هذا السؤال.
من أجل حل المشكلة ، يجدر إبراز العديد من المتطلبات الأساسية:
- لن يكون للنموذج 29 فبراير => 365 يومًا في السنة في النموذج
- كل يوم من أيام 365 محتملة على حد سواء.
بالطبع ، ليس من الواقعي تمامًا أن تكون أعياد الميلاد محتملة على حد سواء - هناك تأثيرات موسمية تؤثر على تواريخ ولادة الأطفال ، أعتقد أنه يمكنك بنفسك تخمين ما ...
معظم الناس يجيبون بشكل حدسي على سؤال المشكلة: 180. يبدو منطقيًا ، هناك حاجة إلى 180 شخصًا للحصول على احتمالية 0.5 أعياد ميلاد متطابقة (365 يومًا إجمالاً). كل من لم يسمع عن مفارقة عيد الميلاد أبدًا يتعلق بهذا الحدس. الإجابة الصحيحة هي في الواقع أقل بكثير من 180 ، وحتى 150 ، وحتى 100: 23.
مطلوب عيد ميلاد مطابق واحد على الأقل - لذلك يمكنني العثور على احتمال عدم وجود أعياد ميلاد مطابقة:...
الفكرة هي: أن آخذ الشخص الأول وأتذكر عيد ميلاده ، ثم الثاني وأحتسب احتمال أن عيد ميلاده لا يتزامن مع عيد ميلاد الأول ؛ أبعد من الثالث وأنا أحسب احتمال أن عيد ميلاده لا يتزامن مع أعياد ميلاد الأول والثاني.
عند حل المعادلة ، تبين أن هناك حاجة إلى 23 شخصًا واحتمال تزامن أعياد الميلاد سيكون 0.5073 ، مع 100 شخص ، الاحتمال هو 0.9999.
دعونا نرى المفارقة في بيانات VK؟
من الناحية النظرية ، مع 23 شخصًا ، فإن احتمال تزامن أعياد الميلاد هو 0.5073 ، مع 50 شخصًا 0.97 ، و 100 0.99. دعونا نتحقق من ذلك من خلال VK API.
1. اخترت مجتمع كبير في VK. قررت أخذ مجموعة MDK على فكونتاكتي ...
أولاً ، أقوم بإنشاء ملف csv بالأعمدة التي أحتاجها.
with open('vk_data.csv', 'w') as new_file:
# csv
fieldnames = ['id', 'bdate', 'bmonth', 'byear', 'dandm']
csv_writer = csv.DictWriter(new_file, fieldnames=fieldnames, delimiter=',')
csv_writer.writeheader()
newDict = dict()أقوم بتسجيل الدخول إلى VK عبر واجهة برمجة التطبيقات وتعيين الجمهور الذي أحتاج إليه
vk_session = vk_api.VkApi('username', 'password')
vk_session.auth()
vk = vk_session.get_api()
vk_group = vk.groups.getMembers(group_id = 'mudakoff', fields = 'bdate')
نبدأ تحليل VKontakte ، تسمح لك واجهة برمجة التطبيقات الخاصة بهم بتحليل 1000 مستخدم فقط ، لذلك أقوم بإنشاء حلقة.
for i in range(0, 20):
vk_group = vk.groups.getMembers(group_id = 'mudakoff', offset = 1000 * i, fields = 'bdate')
for k in range(0, 1000):
try:
new_file.write(str(vk_group['items'][k]["id"]) + ',' + str(vk_group['items'][k]["bdate"]).replace('.', ','))
new_file.write('\n')
except:
passنظريا ، افترضنا أن أعياد الميلاد محتملة على حد سواء ، ولكن ماذا يحدث في الممارسة؟ سأبني الرسم البياني لأعياد الميلاد.
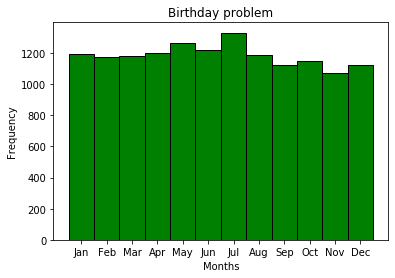
أعياد الميلاد حسب الشهر ليست أحداثًا قابلة للتوازن ، وهو أمر منطقي بشكل عام - هذا مجرد شرط أساسي لحل مشكلة عيد الميلاد. من الواضح أنه ستكون هناك أحداث موسمية مختلفة لمواقع مختلفة. لسبب ما ، يوليو هو الشهر الأكثر شعبية في عيد ميلاد مشتركي MDK.
سوف أقوم بتقدير تجريبي لاحتمال وجود شخصين على الأقل في نفس المجموعة في مجموعة من 50 شخصًا اعتباطيًا. للقيام بذلك ، كتبت دورة تحدث خلالها عينة فرعية من 50 سطرًا من الجدول. لهذه الخطوط الخمسين داخل الشرط ، راجعت مباراة أعياد الميلاد. إذا تطابق ، ثم تذكرته في متغير العداد ، والذي سوف أقسمه بعد ذلك على طول الدورة للحصول على الاحتمال.
fifty = df["dandm"].sample(n = 50)
for i in range(0, 1000):
fifty = df["dandm"].sample(n = 50)
for j in fifty.duplicated():
if j == True:
counter = counter + 1
break
print(':', counter / 1000)يتم الحصول على الاحتمالية في منطقة 0.97 ، والتي تتزامن مع البيانات النظرية.
انتاج |
كان من المثير للاهتمام أن نرى كيف ترتبط النظرية بالتجربة ، وفي هذه الحالة تؤكد البيانات النظرية. وتجدر الإشارة إلى أن النتيجة تمثيلية ، لأن العينة كبيرة بما يكفي - 20000 شخص.
مصادر
- جامعة هارفرد. مشكلة عيد الميلاد ، خصائص الاحتمال | الإحصائيات 110. عنوان URL: www.youtube.com/watch؟v=LZ5Wergp_PA&t=150s . تم الوصول إليه: 07/08/2020
- مشكلة عيد الميلاد. URL: en.wikipedia.org/wiki/Birthday_problem . الوصول إليها: 07/08/2020>