يساعد المنظور الهندسي الجديد في تقديم مشكلة المستطيل القديمة

اكتشف جوشوا غرين وأندرو لوب ، الملل في الحجر الصحي ، كيفية إثبات أحد المتغيرات في نظرية الربط المستطيل

هل يمكن العثور على جميع أنواع المستطيلات في حلقة مغلقة؟



في منتصف شهر مارس، الرياضيات جوشوا غرين و أندرو لوب وجدوا أنفسهم في وضع مماثل - مقفل داخل أربعة جدران، في محاولة للتكيف مع وباء فيروس كورونا المتنامية. قرروا التعامل معها من خلال الخوض في أبحاثهم.



قال جرين ، الأستاذ بكلية بوسطن كوليدج: "أعتقد أن الوباء كان نوعاً من العوامل المحفزة لهذه العملية". "قررنا أنه سيكون من الأفضل القيام بنوع من العمل المشترك الذي يمكن أن يدعمنا."



كانت إحدى المشاكل التي قرر الصديقان معالجتها هي نوع مختلف من السؤال الهندسي الذي ظل بدون إجابة لأكثر من مائة عام.



قال - "هذه المهمة بسيطة للغاية في الصياغة والفهم ، ولكن من الصعب جدا حلها"إليزابيث دين من واشنطن وجامعة لي.



يبدأ كل شيء بحلقة مغلقة - أي مسار منحني له نفس البداية والنهاية. تجادل المهمة التي قام بها Green و Lobb بشكل أساسي في أنه في أي مسار من هذا القبيل توجد مجموعات من أربع نقاط تشكل رؤوس مستطيل من أي نسبة معينة.



وبينما تبدو هذه "مشكلة الربط المستطيل" وكأنها سؤال يستطيع أي طالب في المدرسة الثانوية مع حاكم وبوصلة التعامل معه ، فقد قاوم محاولات الرياضيات الأكثر إلحاحًا لعقود عديدة. وعندما تولى جرين ولوب المسؤولية ، لم يكن لديهما سبب لتوقع أي شيء آخر.



قال غرين إنه من بين جميع المشاريع الصعبة التي عمل عليها ، "كان هذا المشروع الأقل واعدة في رأيي".



لكن الوباء نما ، وأجرى جرين ولوب ، اللذان يعملان في جامعة دورهام في إنجلترا ومعهد أوكيناوا للعلوم والتكنولوجيا ، على التوالي ، محادثات تكبير أسبوعية وسرعان ما أنتجوا العديد من الأفكار. ثم في 19 مايو ، عندما أعيد فتح أجزاء كثيرة من العالم ، نشروا قرارهم .



دليلهم النهائي ، الذي يظهر أنه يمكن العثور على مستطيلات بالفعل ، يأخذ هذه المشكلة إلى مستوى هندسي مختلف تمامًا. وهناك هذا السؤال العنيد يسلم بسهولة.



قال ريتشارد شوارتز من جامعة براون "إنه أمر غريب جدا" . "كانت هذه الفكرة مثالية لهذه المهمة."

إعادة التفكير في المستطيلات

ترتبط مشكلة أوتاد المستطيل ارتباطًا وثيقًا بالسؤال الذي طرحه عالم الرياضيات الألماني أوتو توبليتز في عام 1911. وتوقع أنه في أي منحنى مغلق يمكنك العثور على أربع نقاط ، والتي يمكنك الحصول على مربع. سؤاله حول "الأوتاد المربعة" لا يزال مفتوحًا.



قال غرين: "هذه مهمة قديمة ومحبطة لا يمكن اختراقها بأي شكل من الأشكال".



لفهم مدى تعقيد المشكلة ، من المهم معرفة خصائص المنحنيات التي يتم أخذها بعين الاعتبار في مشكلة الربط المربّع - وهذا مهم أيضًا لإثبات Green و Lobb.



حل هذان الزوجان مشكلة المنحنيات المغلقة "المستمرة" و "السلسة". الاستمرارية تعني عدم الراحة. نعومة تعني الاستمرارية ولا زوايا. من المحتمل أن ترسم منحنى سلس ومستمر إذا جلست على مكتبك بورق وقلم رصاص. قال غرين إنهم "أسهل للعمل معهم".



تختلف المنحنيات المستمرة السلسة عن المنحنيات المستمرة ببساطة ، ولكنها ليست سلسة ، مثل تلك الموجودة في تخمين Toeplitz للأوتاد مربعة. يمكن أن يكون لهذا المنحنى زوايا - نقاط ينحرف فيها المنحنى فجأة ويذهب في اتجاه مختلف. أحد الأمثلة الرئيسية للمنحنى مع العديد من الزوايا هو منحنى كسور فليكتال كوتش.في الواقع ، تتكون من بعض الزوايا. لا يمكن تحليل ندفة ثلج Koch والمنحنيات الأخرى المماثلة باستخدام الطرق الجبرية ، مما يجعل من الصعب دراستها بشكل خاص.



قال دين: "بعض المنحنيات المستمرة [غير الناعمة] مثيرة للاشمئزاز".



ومع ذلك ، فإن المشكلة التي تم حلها بواسطة Green و Lobb تنتمي إلى منحنيات ناعمة وبالتالي مستمرة. وبدلاً من معرفة ما إذا كانت هناك دائمًا أربع نقاط على مثل هذه المنحنيات التي تشكل مربعًا - للحصول على منحنيات مستمرة سلسة تم حل هذه المشكلة في عام 1929 - درسوا شيئًا آخر: ما إذا كانت هناك دائمًا أربع نقاط على مثل هذه المنحنيات التي تشكل مستطيلًا لأي النسب ، أي مع أي نسبة عرض إلى ارتفاع. بالنسبة للمربع ، هذه النسبة هي 1: 1 ، لأجهزة التلفزيون عالية الدقة - 16: 9.







جاء أول اختراق كبير في مشكلة الربط المستطيل في أدلة تم العثور عليها في أواخر السبعينيات بواسطة هربرت فون. عرضت طريقة جديدة للنظر في هندسة المستطيلات وقدمت العديد من الطرق التي تم استخدامها لاحقًا من قبل علماء الرياضيات الآخرين ، بما في ذلك جرين ولوب.



قال غرين: "الكل يعرف هذا الدليل". "إنه تقريبا فلكلوري ، تتعلم عن هذه الأشياء من خلال مناقشة كل شيء على مائدة العشاء."



بدلاً من تخيل مستطيل على أنه أربع نقاط متصلة ، تصور فون أنه زوجان من النقاط في علاقة مع بعضها البعض.







تخيل مستطيلاً مع القمم ABCD. في ذلك ، المسافة بين النقاط AC (على القطر) تساوي المسافة بين النقاط BD (على القطر الآخر). أيضا ، تتقاطع هذه الأقطار بالضبط في المنتصف.



لذلك ، عند البحث عن مستطيلات في حلقة مغلقة ، يمكنك البحث عن أزواج من النقاط التي تقع في نهايات مقاطع الخط نفسها المتقاطعة في المنتصف. للعثور عليها ، من المهم التوصل إلى طريقة منهجية لوصفها.







لفهم ما يعنيه هذا ، لنبدأ بشيء أبسط. خذ خط الأعداد. دعنا نختار نقطتين عليه - دعنا نقول الرقمين 7 و 8 - وننشئهما كنقطة واحدة على المستوى العددي (7 ، 8). يمكننا أيضًا بناء نقاط تتكون من زوج من الأرقام المتطابقة (7 ، 7). الآن دعنا نفكر في جميع أزواج الأرقام الممكنة التي يمكن العثور عليها في سطر الأرقام (وهناك الكثير منها!). إذا قمنا ببناء جميع أزواج هذه الأرقام ، فسنملأ مستوى الرقم بالكامل. هناك طريقة أخرى للتعبير عن هذا وهي أن نقول أن مستوى الأرقام "يعيّن" ، أي أنه يجمع كل أزواج الأرقام في سطر الأرقام بطريقة مرتبة.



قام فون بعمل مماثل مع أزواج من النقاط على منحنى مغلق. إنه ، مثل خط الأرقام ، أحادي البعد ، يغلق على نفسه فقط. لقد أدرك أنه إذا أخذت أزواجًا من النقاط بمنحنى ، وقمت ببناء شكل منها (ولا يهم أيهما هو إحداثيات x وأيها هو y) ، فلن تعمل الطائرة. بدلاً من ذلك ، تحصل على شكل غير متوقع - شريط موبيوس ، سطح ثنائي الأبعاد مع جانب واحد فقط.







وهذا منطقي إلى حد ما. لفهم السبب - حدد زوج من النقاط على المنحنى ، وقم بتسميتها x و y. انتقل الآن من س إلى ص ، وانتقل على طول جزء واحد من المنحنى ، وفي نفس الوقت - من ص إلى س ، تتحرك على عكس ذلك. في هذه العملية ، سوف تمر عبر جميع أزواج النقاط على المنحنى ، وتبدأ وتنتهي على زوج غير مرتبة (س ، ص). لكن هذا سيعيدك إلى البداية - فقط التسلسل النهائي للنقاط سيكون عكس الترتيب الأولي. حلقة من النقاط المضطربة التي تغير الاتجاه إلى العكس هو جوهر شريط Möbius.



يمنح هذا الشريط علماء الرياضيات شيئًا جديدًا يمكن تحليله كجزء من مشكلة الربط المستطيل. استخدم فون هذه الحقيقة لإثبات أنه على أي منحنى هناك مجموعة واحدة على الأقل من أربع نقاط تشكل مربعًا.

إجابات رباعية الأبعاد

يعتمد دليل جرين ولوب على عمل فون. ومع ذلك ، فإنه يجمع أيضًا بين عدة نتائج إضافية ، بعضها حديث نسبيًا. البرهان النهائي هو مثل أداة دقيقة ، تعتمد النتيجة المرجوة على مزيج مدروس بعناية من الأفكار.



جاء أحد المكونات الرئيسية الأولى لإثباتهم في نوفمبر 2019 ، عندما نشر طالب الدكتوراه في جامعة برينستون كول هوجلميير الورقةيوضح طريقة جديدة لتحليل شريط موبيوس المستخدم من قبل فون. استخدم عملية رياضية تعرف باسم التعشيش ، وهي عندما نأخذ كائنًا ونعرضه على مساحة هندسية. ونتيجة لذلك ، أخذ Green and Lobb تقنية Hugelmeyer ونقلها إلى مساحة هندسية أخرى. ولكن لفهم ما فعلوه ، تحتاج أولاً إلى فهم ما فعله.



إليك مثال بسيط على التعشيش.



لنبدأ بخط أحادي البعد. يتم تعريف كل نقطة في الخط المستقيم برقم واحد. الآن سنقوم بتضمين هذا الخط في مساحة ثنائية الأبعاد - أي أننا سنرسمه على مستوى.



بعد تضمين خط مستقيم على المستوى xy ، يتم تحديد كل نقطة فيه بالفعل برقمين - إحداثيات x و y ، التي تصف مكان النقطة بالضبط على المستوى. يمكنك الآن تحليل الخط باستخدام تقنيات الهندسة ثنائية الأبعاد.



كانت فكرة Hugelmeier أن تأخذ شيئًا مثل شريط Möbius ، ولكن تضمينه في مساحة 4 ، حيث تسمح لك خصائص الهندسة 4 الأبعاد بإثبات النتائج التي تريدها.



"بشكل أساسي ، لديك شريط Mobius ، وتحتاج إلى تعيين أربعة إحداثيات لكل نقطة. قال لوب: "سيكون شيئًا مثل عنوان نقطة في الفضاء رباعي الأبعاد".



عيّن Hugelmeyer هذه العناوين بطريقة تجعل الوصول إلى الهدف الرئيسي أسهل ، والعثور على مستطيلات على منحنى. يمكننا القول أنه خصص لكل نقطة على المنحنى شيئًا مثل العنوان البريدي - الولاية والمدينة واسم الشارع ورقم المنزل.



للقيام بذلك ، بدأ من نقطة معينة على شريط Mobius وأخذ النقطتين على المنحنى المغلق الأصلي الذي أشارت إليه. ثم وجد نقطة الوسط لقطعة الخط التي تربط هذه النقاط ، وحدد إحداثياتها س وص. لقد حصلنا على أول قيمتين للعنوان رباعي الأبعاد (الولاية والمدينة).



ثم قام بقياس المسافة بين النقطتين الأصليتين على المنحنى. أصبح هذا الطول القيمة الثالثة للعنوان رباعي الأبعاد (اسم الشارع). أخيرًا ، قام بحساب الزاوية بين جزء الخط الذي يربط بين النقطتين الأصليتين والمحور السيني. أصبحت هذه الزاوية القيمة الرابعة للعنوان رباعي الأبعاد (رقم المنزل). تخبرك هذه القيم الأربع بكل شيء عن زوج من النقاط على المنحنى.







يبدو هذا التمرين صعبًا بما فيه الكفاية ، لكنه حقق ثماره بسرعة. أخذ Hugelmeyer شريط Mobius المرفق وأداره. تم تحريك شريط Mobius المستدير بالنسبة إلى موضعه الأصلي ، وتتقاطع نسختا الشريط. نظرًا لأن الدوران حدث في مساحة رباعية الأبعاد ، فمن الصعب تصور شكل التقاطع الذاتي لشريط موبيوس - ولكن من السهل وصفه رياضيًا.



كان لهذا التقاطع أهمية كبيرة. عندما يتم فرض نسختين من شريط Mobius على بعضهما البعض ، يمكن العثور على أزواج من النقاط على المنحنى المغلق الأصلي ، لتشكيل القمم الأربعة للمستطيل.



لماذا ا؟



أولاً ، تذكر أنه يمكن تمثيل المستطيل على أنه زوجان من النقاط مع مركز مشترك للتقاطع بين مقاطع من نفس الطول تربط بينهما. هذه هي المعلومات التي تم ترميزها في القيم الثلاث الأولى من العنوان رباعي الأبعاد المخصص لكل نقطة من شريط Möbius المتداخل.



ثانيًا ، في الفضاء رباعي الأبعاد ، يمكنك الكشف عن شريط Mobius بطريقة لتغيير إحداثيات واحدة فقط من كل نقطة في عنوانها رباعي الأبعاد - يتغير رقم المنزل ، ولكن يبقى الشارع والمدينة والولاية. كمثال ، تذكر أنه إذا أخذت لبنة ، ضعها أمامك ، ثم حركتها إلى اليمين ، عندها فقط ستتغير إحداثيها x ، ولكن ليس y أو z.





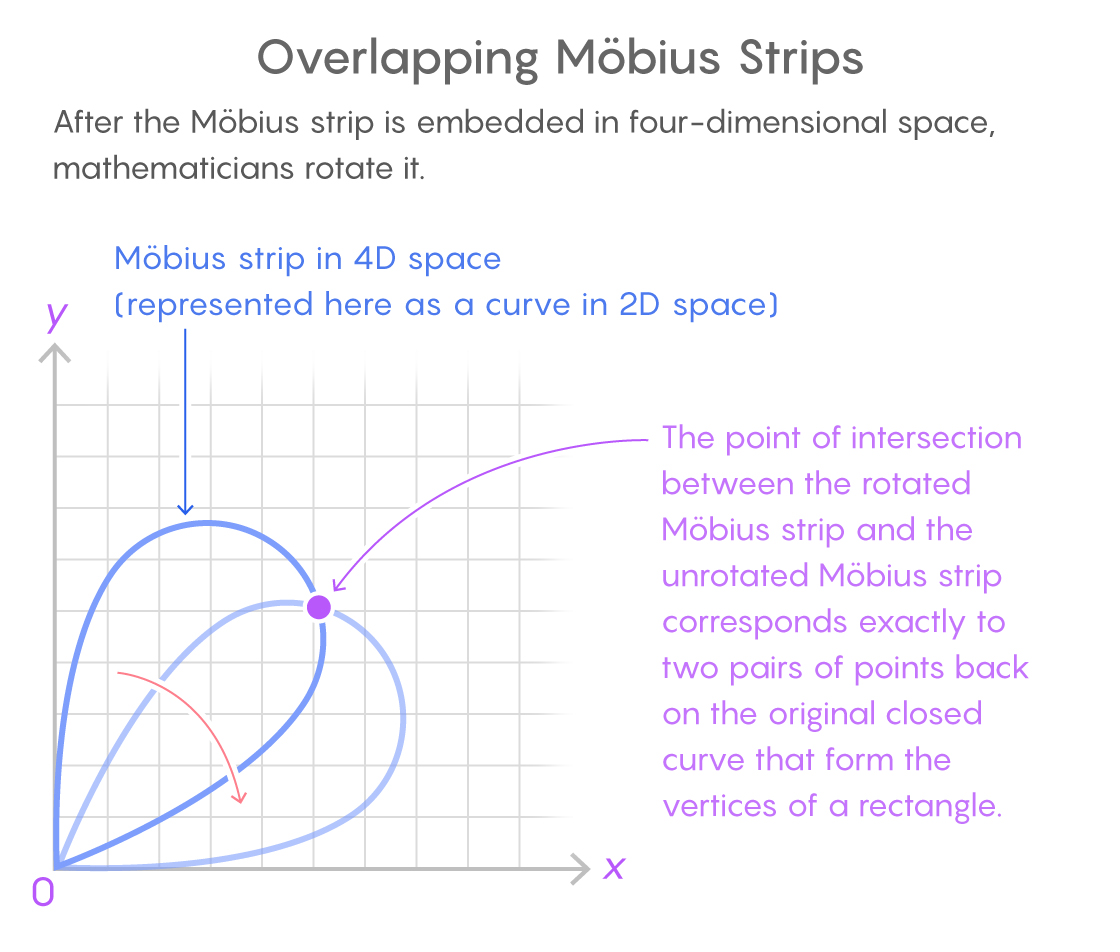
يشار إلى شريط Möbius في مساحة رباعية الأبعاد هنا بمنحنى ثنائي الأبعاد. تقابل نقطة تقاطع النسختين أزواج من النقاط على المنحنى المغلق الأصلي الذي يشكل مستطيلاً.



أوضح Hugelmeyer كيفية تدوير شريط Mobius في مساحة رباعية الأبعاد بحيث لا تتغير الإحداثيات التي تشير إلى منتصف خطوط الخطوط التي تربط الأزواج - كما تفعل الإحداثيات التي تشير إلى المسافة بين أزواج النقاط. تغير دورانها فقط الإحداثيات الأخيرة - التي تحتوي على معلومات حول الزاوية التي يوجد بها الجزء الذي يربط النقاط.



ونتيجة لذلك ، فإن تقاطع النسخة المستديرة من شريط Möbius وأصلها يتوافق تمامًا مع زوجين من النقاط الموجودة على منحنى مغلق ، مع وجود مركز مشترك (تقاطعات الأجزاء التي تربطها) وتقع على نفس المسافة من بعضها البعض. أي أن هذا التقاطع يتوافق مع القمم الأربعة للمستطيل على المنحنى.



لطالما استخدمت استراتيجية استخدام تقاطع مسافتين للعثور على النقاط الصحيحة في العمل على مشاكل الأوتاد المربعة والمستطيلة.



قال دين "عند تقاطع هذه المساحات هو المطلوب". "الكثير من الأدلة من تاريخ الأوتاد المربعة لديها هذه الفكرة."



استخدم Hugelmeyer استراتيجية تقاطع في بيئة رباعية الأبعاد وحصل على أكثر من أي شخص قبله. يمكن تدوير شريط Mobius بأي زاوية من 0 ° إلى 360 ° ، وأثبت أن ثلث كل هذه الدورات يؤدي إلى تقاطع النسخة الأصلية والنسخة المستدارة. هذا يعادل القول أنه يمكنك العثور على مستطيلات على منحنى مغلق مع ثلث جميع نسب العرض إلى الارتفاع الممكنة.



قال جرين: "ننسب الفضل إلى كول للتفكير في وضع شريط موبيوس في مساحة 4D واستخدام تقنيات 4D".



في الوقت نفسه ، اتضح أن نتيجة Hugelmeier استفزازية: إذا كان الفضاء رباعي الأبعاد مفيدًا جدًا للعمل مع هذه المشكلة ، فلماذا كان مفيدًا لثلث المستطيلات فقط؟



قال غرين "بعد كل شيء ، يجب أن تكون هناك طريقة للحصول على الثلثين المتبقيين". - ولكن كيف؟"

نهج تأملي

كان غرين ولوب مهتمين بمشكلة أوتاد مستطيلة حتى قبل أن يرسلهما الوباء إلى المنزل. في فبراير ، استضاف لوب مؤتمرًا في معهد أوكيناوا للعلوم والتكنولوجيا ، والذي حضره جرين أيضًا. قضى الزوجان يومين يتحدثان عن هذه المهمة. بعد ذلك ، ناقشوا ذلك لمدة أسبوع آخر ، على طول الطريق لرؤية مناظر طوكيو.



قال لوب: "لم نتوقف عن مناقشة هذه القضية". "ذهبنا إلى المطاعم والمقاهي والمتاحف ، وكان لدينا من وقت لآخر أفكار حول هذا."



واصلوا مناقشاتهم حتى بعد حبسهم في منازلهم. كانوا يأملون في إثبات أن أي دوران لشريط موبيوس سيعطي نقطة تقاطع - وهو ما يعادل العثور على مستطيلات بأي نسبة.



في منتصف أبريل ، شكلوا استراتيجية. يعني ذلك تضمين الشريط في نوع خاص من الفضاء الرباعي الأبعاد. التعشيش المنتظم يعني أنك تضع الكائن المطلوب بأي شكل من الأشكال. تخيل عدد الطرق التي يمكنك من خلالها تضمين منحنى مغلق أحادي البعد في مستوى ثنائي الأبعاد - حيث أن عددهم لا نهائي ، حيث يوجد عدد لا نهائي من الطرق التي يمكنك من خلالها وضع خيط مقيد في حلقة على طاولة.



ولكن دعنا نقول أن السطح ثنائي الأبعاد الذي تداخل فيه الحلقة له هيكله الخاص. تخيل ، على سبيل المثال ، خريطة بها أسهم (أو ناقلات) تشير إلينا في أي اتجاه وبأي سرعة تهب الرياح على سطح الأرض. الآن لديك سطح ثنائي الأبعاد بمعلومات أو بنية إضافية في كل نقطة.



ثم يمكنك إدخال قيود - يجب وضع RFP أحادي البعد على الخريطة بحيث يتبع دائمًا اتجاهات الأسهم على الخريطة.



قال شوارتز: "أنت تحد من الأشياء بحيث يتبع المنحنى هذه المتجهات". والآن لديك طرق أقل لوضع المنحنى.







قد تفرض المساحات الهندسية الأخرى قيودًا مختلفة. المهم لعمل جرين ولوب كان يسمى. مساحة تأملية .



ظهر هذا المفهوم الهندسي لأول مرة في القرن التاسع عشر عند دراسة الأنظمة الفيزيائية مثل الكواكب المدارية. يتم تحديد موقع كوكب يتحرك في الفضاء ثلاثي الأبعاد من خلال ثلاثة إحداثيات. ولكن ، كما لاحظ عالم الرياضيات الأيرلندي وليام روان هاميلتون، في كل نقطة من مسار حركة الكوكب ، يمكنك أيضًا وضع ناقل يشير إلى زخمه.



في الثمانينيات ، طور عالم الرياضيات السوفياتي والروسي فلاديمير إيغوريفيتش أرنولد دراسة الهندسة الانقباضية . لقد أدرك أن المساحات الهندسية لبنية متشابكة ، عندما يتم تدويرها ، تتقاطع مع نفسها في كثير من الأحيان أكثر من المساحات التي لا تحتوي على مثل هذا الهيكل.



كان هذا مثاليًا لـ Green و Lobb ، حيث أرادوا حل مشكلة الربط المستطيل لجميع النسب ، مما يثبت أن نسخة مستديرة من شريط Mobius المتقاطع تتقاطع أيضًا في كثير من الأحيان. لذلك بدأوا في محاولة لتضمين شريط Möbius ثنائي الأبعاد في مساحة عرضية رباعية الأبعاد. قال غرين: "كانت الفكرة الجديدة جذريًا هي التعامل مع هذه المشكلة من وجهة نظر الهندسة الانعكاسية". "وهذا غير كل شيء."



بحلول نهاية أبريل ، قرر جرين ولوب أنه من الممكن تضمين شريط موبيوس في مساحة عرضية رباعية الأبعاد بحيث تتماشى مع هيكلها. بعد ذلك ، يمكن أن يبدأوا في استخدام أدوات الهندسة المعقدة ، والتي يرتبط الكثير منها مباشرة بمسألة التقاطعات الذاتية.



قال لوب: "إذا كان يمكن صنع شريط موبيوس لاتباع القواعد النظرية ، فيمكن استخدام بعض النظريات النظرية".



كان Green و Lobb واثقين من أنهما يمكنهما تحسين نتيجة Hugelmeyer - أي إثبات أن التقاطع لا يحدث في ثلث الزوايا فقط. هذا يعني أنه من خلال نقاط المنحنى سيكون من الممكن عمل مستطيلات بأكثر من ثلث جميع النسب الممكنة.



قال لوب: "عندما توصلنا إلى هذه الفكرة ، أصبح من الواضح أن شيئًا ما سيحدث".



ومع ذلك ، اتضح أن نتائجهم أكثر عمومية ، وبدت أسرع بكثير مما توقعوا. كل ذلك بفضل كائن رياضي غريب - زجاجة كلاين ، التي لها في سياق الهندسة التأملية خاصية مهمة واحدة.

اتصال زجاجة كلاين

زجاجة Klein هي سطح ثنائي الأبعاد يشبه إبريقًا عصريًا. إنه ، مثل شريط Mobius ، له سطح واحد فقط ، ويمكن صنعه عن طريق لصق شريحتين من Mobius. أي زجاجة كلاين يمكنك جمعها ووضعها على مكتبك (كما يفعل العديد من علماء الرياضيات) تعبر نفسها. من المستحيل وضع زجاجة كلاين في مساحة ثلاثية الأبعاد بحيث لا تعبر نفسها.



قال شوارتز: "يجب أن تكون زجاجة كلاين سطحًا ، لكن مقبضها يحتاج إلى اختراق الزجاجة للانتقال من الخارج إلى الداخل".



ومع ذلك ، ليس هذا هو الحال بالضرورة. يمكن تداخل زجاجة Klein في مساحة 4D بحيث لا تتقاطع مع نفسها. يوفر البعد الرابع مساحة للمناورة ، ويمكن لزجاجة Klein تجاوز نفسها. يمكن مقارنة ذلك بكيفية سير شخصين تجاه بعضهما البعض في خط أحادي البعد ، فلا يمكنهم تجنب الاصطدام ، ولكن إذا مشوا على أرضية ثنائية الأبعاد ، فيمكنهم بسهولة الابتعاد.







في مايو ، استدعى غرين ولوب حقيقة واحدة عن زجاجة كلاين - لا يمكن تضمينها في مساحة تأملية رباعية الأبعاد بحيث لا تتقاطع مع نفسها [من عمل عالم رياضيات روسي آخر ، Vsevolod Viktorovich Shevchishinبشأن تضمين Lagrangian لزجاجة Klein في مساحة رباعية الأبعاد / تقريبًا. ترجم.]. وبعبارة أخرى ، لا توجد زجاجة كلاين بدون تقاطع ذاتي يفي بجميع متطلبات المساحة المتناظرة. أصبحت هذه الحقيقة مفتاح البرهان. قال غرين: "لقد كانت عصا سحرية".



ولهذا السبب. لقد أظهر Green و Lobb بالفعل أنه من الممكن تضمين شريط Mobius في مساحة عرضية رباعية الأبعاد بحيث تلبي متطلباته. كانوا بحاجة فقط لمعرفة ما إذا كان كل منعطف من شريط Mobius يتقاطع مع النسخة الأصلية.



ومع ذلك ، فإن شريطين موبيوس المتقاطعين يعادلان زجاجة كلاين ، التي تتقاطع مع نفسها في مثل هذه المساحة. وإذا قمت بتدوير شريط Mobius بحيث لا تتقاطع النسخة التي تم تدويرها مع النسخة الأصلية ، فستحصل على زجاجة Klein لا تتقاطع مع نفسها. لكن زجاجة كلاين هذه لا يمكن أن توجد في مساحة عرضية رباعية الأبعاد. لذلك ، يجب أيضًا أن يتقاطع أي دوران محتمل لشريط Möbius المتداخل - أي على كل منحنى سلس مغلق ، يمكن العثور على أربع نقاط تشكل مستطيلًا بأي نسب.



تضرب نهاية الدليل القارئ مثل الانهيار الجليدي.



قال دين: "لقد تم إعداده وإعداده وإعداده ثم نخره ، والدليل جاهز".



برهان جرين ولوب هو مثال جيد على كيفية حل المشكلة غالبًا ما يعتمد على إيجاد وجهة النظر الصحيحة. لم تتمكن أجيال من علماء الرياضيات من معالجة هذه النسخة من مشكلة الربط المستطيل لأنهم حاولوا حلها في ظروف هندسية أكثر تقليدية. عندما جلب غرين ولوب المشكلة إلى العالم المفعم بالحل ، تم حلها بسهولة.



قال غرين: "هذه المشاكل ، التي ظهرت في عقد 1910 وعشرينيات القرن العشرين ، لم يكن لديها منصة مناسبة للتفكير فيها". "والآن بدأنا نفهم أنهم في الواقع تجسيد خفي لظاهرة التأمل".