👐🏻 🆓 💥 كشف التصادم ونظرية محور التقسيم 🐲 🙏🏼 👌🏿

في الوقت الحاضر ، تعتبر أجهزة الكمبيوتر أجهزة كمبيوتر قوية

قادرة على أداء ملايين العمليات في الثانية. وبطبيعة الحال ، لا يمكنك الاستغناء عن محاكاة العالم الحقيقي أو اللعبة. تتمثل إحدى مشكلات النمذجة والمحاكاة الحاسوبية في تحديد تصادم شيئين ، ويتم تحقيق أحد الحلول من خلال النظرية على المحور الفاصل.

ملحوظة. ستعطي المقالة مثالًا مع 2 متوازي السطوح (فيما يلي - المكعبات) ، ولكن سيتم الحفاظ على فكرة الأشياء المحدبة الأخرى.

ملحوظة. سيتم تنفيذ جميع في الوحدة.

قانون 0. النظرية العامة

أولاً ، يجب أن تتعرف على " نظرية الفصل المفرط للطائرة " التي ستكون أساس الخوارزمية.

نظرية. لا تتقاطع هندستان محدبتان إذا وفقط إذا كان هناك سطح زائد بينهما يفصل بينهما. يسمى المحور المتعامد للقطعة

الزائدة الفاصلة بمحور التقسيم ، ولا تتقاطع إسقاط الأشكال عليه.

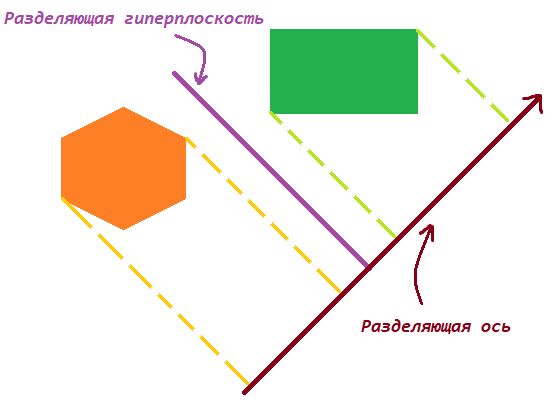
محور التقسيم (حالة ثنائية الأبعاد)

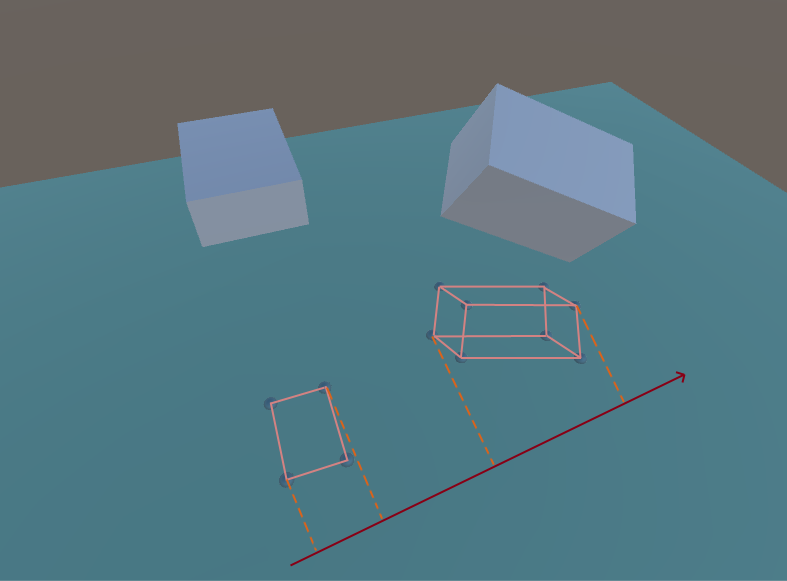
محور التقسيم (حالة ثلاثية الأبعاد)

قد تلاحظ أن الإسقاطات على محور التقسيم لا تتقاطع.

خاصية. سيكون محور التقسيم المحتمل في المجموعات التالية:

معايير الطائرة لكل مكعب (أحمر)
منتج متجه من حواف المكعبات $\{[\vec{x},\vec{y}] : x∈X, y∈Y\}$ ،

حيث X هي حواف المكعب الأول (أخضر) و Y هو الثاني (أزرق).

يمكننا وصف كل مكعب مع بيانات الإدخال التالية:

إحداثيات مركز المكعب
أبعاد المكعب (الارتفاع ، العرض ، العمق)
رباعي المكعب

لنقم بإنشاء فئة إضافية لهذا ، ستوفر مثيلاتها معلومات حول المكعب.

public class Box
{
    public Vector3 Center;
    public Vector3 Size;
    public Quaternion Quaternion;

    public Box(Vector3 center, Vector3 size, Quaternion quaternion)
    {
       this.Center = center;
       this.Size = size;
       this.Quaternion = quaternion;
    }
    //  , 
    //      GameObject
    public Box(GameObject obj)
    {
        Center = obj.transform.position;
        Size = obj.transform.lossyScale;
        Quaternion = obj.transform.rotation;
    }

}

قانون 1. Quaternions

كما هو الحال في كثير من الأحيان ، يمكن أن يدور الجسم في الفضاء. من أجل العثور على إحداثيات القمم ، مع مراعاة دوران المكعب ، تحتاج إلى فهم ما هو رباعي.

Quaternion عبارة عن رقم فرعي مركب يحدد دوران كائن في الفضاء.

w + x i + y j + z k

$w+xi+yj+zk$

يمثل الجزء التخيلي (x، y، z) متجهًا يحدد اتجاه الدوران ، أما

الجزء الحقيقي (w) فيحدد الزاوية التي سيتم بها التدوير.

الاختلاف الرئيسي بين جميع زوايا أويلر المعتادة هو أنه يكفي بالنسبة لنا أن يكون لدينا متجه واحد ، والذي سيحدد اتجاه الدوران ، من ثلاثة ناقلات مستقلة خطياً تقوم بتدوير الكائن في 3 مسافات فرعية.

أوصي مقالين أن تذهب إلى مزيد من التفاصيل حول كواتيرنيون:

واحد

اثنين

الآن أن لدينا فهم الحد الأدنى من كواتيرنيون، دعونا نفهم كيفية تدوير النواقل ووصف وظيفة الدورية متجه مع من أربعة.

صيغة دوران المتجه

{\vec{v}}^{'} = q * \vec{v} * \bar{q}

$\vec{v}' = q * \vec{v} * \overline{q}$

{\vec{v}}^{'}

$\vec{v}'$ هو الناقل المطلوب

\vec{v}

$\vec{v}$ - ناقل أصلي

q

$q$ - رباعي

\bar{q}

$\overline{q}$ - الرباعية العكسية

بادئ ذي بدء ، دعونا نعطي مفهوم الرباعية العكسية على أساس متعامد - إنه رباعي مع جزء وهمي من العلامة المعاكسة.

q = w + x i + y j + z k

$q = w+xi+yj+zk$

\bar{q} = w - x i - y j - z k

$\overline{q} = w-xi-yj-zk$

دعونا نحسب

\vec{v} * \bar{q}

$\vec{v} * \overline{q}$

M = \vec{v} * \bar{q} = (0 + v_{x} i + v_{y} j + v_{z} k) (q_{w} - q_{x} i - q_{y} j - q_{z} k) =

$M = \vec{v}*\overline{q} = (0 + v_xi + v_yj + v_zk)(q_w - q_xi - q_yj - q_zk) =$

= v_{x} q_{w} i + v_{x} q_{x} - v_{x} q_{y} k + v_{x} q_{z} j +

$=\color{red}{v_xq_wi} + \color{purple}{v_xq_x} - \color{blue}{v_xq_yk} + \color{green}{v_xq_zj} +$

+ v_{y} q_{w} j + v_{y} q_{x} k + v_{y} q_{y} - v_{y} q_{z} i +

$+\color{green}{v_yq_wj} + \color{blue}{v_yq_xk} + \color{purple}{v_yq_y} - \color{red}{v_yq_zi} +$

+ v_{z} q_{w} k - v_{z} q_{x} j + v_{z} q_{y} i + v_{z} q_{z}

$+\color{blue}{v_zq_wk} - \color{green}{v_zq_xj} + \color{red}{v_zq_yi} + \color{purple}{v_zq_z}$

الآن سنكتب المكونات الفردية ومن هذا المنتج سنجمع ربعًا جديدًا

M = u_{w} + u_{x} i + u_{y} j + u_{z} k

$M = u_w+u_xi+u_yj+u_zk$

u_{w} = v_{x} q_{x} + v_{y} q_{y} + v_{z} q_{z}

$u_w = \color{purple}{v_xq_x + v_yq_y + v_zq_z}$

u_{x} i = (v_{x} q_{w} - v_{y} q_{z} + v_{z} q_{y}) i

$u_xi = \color{red}{(v_xq_w - v_yq_z + v_zq_y)i}$

u_{y} j = (v_{x} q_{z} + v_{y} q_{w} - v_{z} q_{x}) j

$u_yj = \color{green}{(v_xq_z + v_yq_w - v_zq_x)j}$

u_{z} k = (- v_{x} q_{y} + v_{y} q_{x} + v_{z} q_{w}) k

$u_zk = \color{blue}{(-v_xq_y + v_yq_x + v_zq_w)k}$

دعونا نحسب الباقي ، أي

q * M

$q*M$ والحصول على المتجه المطلوب.

ملحوظة. من أجل عدم التحميل الزائد للحسابات ، نقدم فقط الجزء التخيلي (الموجه) من هذا المنتج. بعد كل شيء ، هي التي تميز المتجه المطلوب.

{\vec{v}}^{'} = q * M = (q_{w} + q_{x} i + q_{y} j + q_{z} k) (u_{w} + u_{x} i + u_{y} j + u_{z} k) =

$\vec{v}' = q*M = (q_w + q_xi + q_yj + q_zk)(u_w + u_xi + u_yj + u_zk) =$

= q_{w} u_{x} i + q_{w} u_{y} j + q_{w} u_{z} k +

$= \color{red}{q_wu_xi} + \color{green}{q_wu_yj} + \color{blue}{q_wu_zk} +$

+ q_{x} u_{w} i + q_{x} u_{y} k - q_{x} u_{z} j +

$+\color{red}{q_xu_wi} + \color{blue}{q_xu_yk} - \color{green}{q_xu_zj} +$

+ q_{y} u_{w} j - q_{y} u_{x} k + q_{y} u_{z} i +

$+\color{green}{q_yu_wj} - \color{blue}{q_yu_xk} + \color{red}{q_yu_zi} +$

+ q_{z} u_{w} k + q_{z} u_{x} j - q_{z} u_{y} i

$+\color{blue}{q_zu_wk} +\color{green}{q_zu_xj} -\color{red}{q_zu_yi}$

دعونا نجمع مكونات المتجه

v_{x}^{'} = q_{w} u_{x} + q_{x} u_{w} + q_{y} u_{z} - q_{z} u_{y}

$v_x' = \color{red}{q_wu_x + q_xu_w + q_yu_z - q_zu_y}$

v_{y}^{'} = q_{w} u_{y} - q_{x} u_{z} + q_{y} u_{w} + q_{z} u_{x}

$v_y' = \color{green}{q_wu_y - q_xu_z + q_yu_w + q_zu_x}$

v_{z}^{'} = q_{w} u_{z} + q_{x} u_{y} - q_{y} u_{x} + q_{z} u_{w}

$v_z' = \color{blue}{q_wu_z + q_xu_y - q_yu_x + q_zu_w}$

v^{'} = (v_{x}^{'}, v_{y}^{'}, v_{z}^{'})

$v' = (v_x', v_y', v_z')$

وبالتالي ، يتم الحصول على المتجه المطلوب. اكتب

الرمز:

private static Vector3 QuanRotation(Vector3 v,Quaternion q)
{
        float u0 = v.x * q.x + v.y * q.y + v.z * q.z;
        float u1 = v.x * q.w - v.y * q.z + v.z * q.y;
        float u2 = v.x * q.z + v.y * q.w - v.z * q.x;
        float u3 = -v.x * q.y + v.y * q.x + v.z * q.w;
        Quaternion M = new Quaternion(u1,u2,u3,u0);
        
        Vector3 resultVector;
        resultVector.x = q.w * M.x + q.x * M.w + q.y * M.z - q.z * M.y;  
        resultVector.y = q.w * M.y - q.x * M.z + q.y * M.w + q.z * M.x;
        resultVector.z = q.w * M.z + q.x * M.y - q.y * M.x + q.z * M.w;
        
        return resultVector;
}

قانون 2. إيجاد رؤوس المكعب

بمعرفة كيفية تدوير ناقل مع رباعي ، لن يكون من الصعب العثور على جميع رؤوس المكعب.

دعنا ننتقل إلى وظيفة إيجاد رؤوس المكعب. دعونا نحدد المتغيرات الأساسية.

private static Vector3[] GetPoint(Box box)
{
        //    
        Vector3[] point = new Vector3[8];

        // 
        //....

        return point;
}

بعد ذلك ، تحتاج إلى العثور على نقطة (نقطة ربط) سيكون من الأسهل العثور على قمم أخرى.

اطرح نصف بُعد المكعب من إحداثيات المركز ، ثم أضف بُعدًا مكعبًا إلى النقطة المحورية.

//...
        //  
        point[0] = box.Center - box.Size/2;
        point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
        point[2] = point[0] + new Vector3(0, box.Size.y, 0);
        point[3] = point[0] + new Vector3(0, 0, box.Size.z);
		
	//     
        point[4] = box.Center + box.Size / 2;
        point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
        point[6] = point[4] - new Vector3(0, box.Size.y, 0);
        point[7] = point[4] - new Vector3(0, 0, box.Size.z);
//...

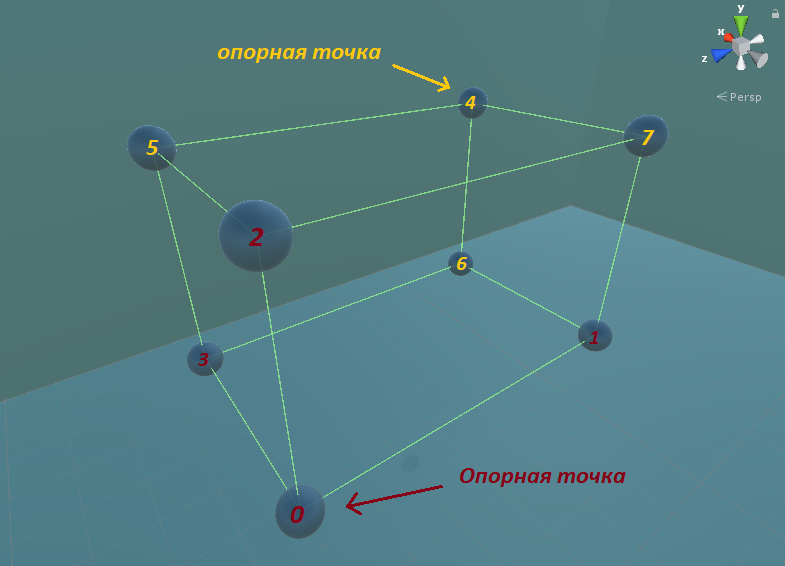
يمكننا أن نرى كيف يتم تشكيل النقاط

بعد العثور على إحداثيات القمم ، فمن الضروري تدوير كل متجه بواسطة الرباعية المقابلة.

//...

        for (int i = 0; i < 8; i++)
        {
            point[i] -= box.Center;//    

            point[i] = QuanRotation(point[i], box.Quaternion);//

            point[i] += box.Center;// 
        }

//...

كود كامل للحصول على القمم

private static Vector3[] GetPoint(Box box)
{
        Vector3[] point = new Vector3[8];
        
        //  
        point[0] = box.Center - box.Size/2;
        point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
        point[2] = point[0] + new Vector3(0, box.Size.y, 0);
        point[3] = point[0] + new Vector3(0, 0, box.Size.z);
		
	//     
        point[4] = box.Center + box.Size / 2;
        point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
        point[6] = point[4] - new Vector3(0, box.Size.y, 0);
        point[7] = point[4] - new Vector3(0, 0, box.Size.z);

        //  
        for (int i = 0; i < 8; i++)
        {
            point[i] -= box.Center;//    

            point[i] = QuanRotation(point[i], box.Quaternion);//

            point[i] += box.Center;// 
        }
        
        return point;
}

دعنا ننتقل إلى الإسقاطات.

قانون 3. البحث عن محاور التقسيم

الخطوة التالية هي العثور على مجموعة المحاور التي تدعي أنها تنقسم.

تذكر أنه يمكن العثور عليه في المجموعات التالية:

الأعراف الطائرة لكل مكعب (أحمر)
منتج متجه من حواف المكعبات $\{[\vec{x},\vec{y}[ : x∈X, y∈Y\}$ حيث X هي حواف المكعب الأول (أخضر) و Y هو الثاني (أزرق).

من أجل الحصول على المحاور اللازمة ، يكفي أن يكون لديك أربعة رؤوس المكعب ، والتي تشكل نظام متعامد من المتجهات. توجد هذه القمم في الخلايا الأربع الأولى من مصفوفة النقاط التي شكلناها في الفصل الثاني.

من الضروري العثور على المعايير المستوية المولدة من المتجهات:

$\vec{a}$ و $\vec{b}$
$\vec{b}$ و $\vec{c}$
$\vec{a}$ و $\vec{c}$

للقيام بذلك ، من الضروري التكرار من خلال أزواج حواف المكعب بحيث تشكل كل عينة جديدة مستوى متعامد لجميع الطائرات السابقة التي تم الحصول عليها. كان من الصعب للغاية بالنسبة لي أن أشرح كيف يعمل ، لذلك قدمت نسختين من التعليمات البرمجية لمساعدتك على الفهم.

يسمح لك هذا الرمز بالحصول على هذه المتجهات والعثور على القيم الطبيعية للطائرات لمكعبين (خيار مفهوم)

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //
        Vector3 A;
        Vector3 B;

        //  
        List<Vector3> Axis = new List<Vector3>();

        //   
        A = a[1] - a[0];
        B = a[2] - a[0];
        Axis.Add(Vector3.Cross(A,B).normalized);
        
        A = a[2] - a[0];
        B = a[3] - a[0];
        Axis.Add(Vector3.Cross(A,B).normalized);
        
        A = a[1] - a[0];
        B = a[3] - a[0];
        Axis.Add(Vector3.Cross(A,B).normalized);
        

        //  
        A = b[1] - b[0];
        B = b[2] - b[0];
        Axis.Add(Vector3.Cross(A,B).normalized);
        
        A = b[1] - b[0];
        B = b[3] - b[0];
        Axis.Add(Vector3.Cross(A,B).normalized);
        
        A = b[2] - b[0];
        B = b[3] - b[0];
        Axis.Add(Vector3.Cross(A,B).normalized);

        //...
}

ولكن يمكنك تسهيل الأمر:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //
        Vector3 A;
        Vector3 B;

	//  
        List<Vector3> Axis = new List<Vector3>();

	//   
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            B = a[(i+1)%3+1] - a[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }
	//  
        for (int i = 1; i < 4; i++)
        {
            A = b[i] - b[0];
            B = b[(i+1)%3+1] - b[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }

        //...
}

علينا أيضًا العثور على جميع المنتجات المتجهة لحواف المكعبات. يمكن تنظيم ذلك من خلال بحث بسيط:

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
        //...
        // 
        //... 

       //    
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            for (int j = 1; j < 4; j++)
            {
                B = b[j] - b[0];
                if (Vector3.Cross(A,B).magnitude != 0)
                {
                    Axis.Add(Vector3.Cross(A,B).normalized);
                }
            }
        }
        return Axis;
}

كود كامل

private static List<Vector3> GetAxis(Vector3[] a, Vector3[] b)
{
	//
        Vector3 A;
        Vector3 B;

	//  
        List<Vector3> Axis = new List<Vector3>();

	//   
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            B = a[(i+1)%3+1] - a[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }
	//  
        for (int i = 1; i < 4; i++)
        {
            A = b[i] - b[0];
            B = b[(i+1)%3+1] - b[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }

        //    
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            for (int j = 1; j < 4; j++)
            {
                B = b[j] - b[0];
                if (Vector3.Cross(A,B).magnitude != 0)
                {
                    Axis.Add(Vector3.Cross(A,B).normalized);
                }
            }
        }
        return Axis;
}

قانون 4. إسقاطات على المحور

لقد وصلنا إلى أهم نقطة. هنا يجب أن نجد إسقاطات المكعبات على جميع محاور التقسيم المحتملة. النظرية لها نتيجة مهمة واحدة: إذا تقاطع الأشياء ، فإن المحور الذي يكون فيه تقاطع إسقاط المكعبات هو الحد الأدنى هو اتجاه (الاصطدام) للتصادم ، وطول مقطع التقاطع هو عمق الاختراق.

لكن أولاً ، تذكر صيغة الإسقاط الحجمي للمتجه v على متجه الوحدة a :

p r o j_{⟨ \vec{a} ⟩} \vec{v} = \frac{(\vec{v}, \vec{a})}{| \vec{a} |}

$proj_\left\langle \vec{a} \right\rangle \vec{v} = \frac{(\vec{v},\vec{a})}{| \vec{a} |}$

private static float ProjVector3(Vector3 v, Vector3 a)
{
        a = a.normalized;
        return Vector3.Dot(v, a) / a.magnitude;
        
}

الآن سنصف وظيفة ستحدد تقاطع الإسقاطات على المحاور المرشحة.

المدخلات هي رؤوس مكعّبين ، وقائمة محاور التقسيم المحتملة:

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
           //     
           //         
        }
        //       ,   ,    
        //    .
}

يتم تعيين الإسقاط على المحور بنقطتين لهما قيم قصوى ودنيا على المحور نفسه:

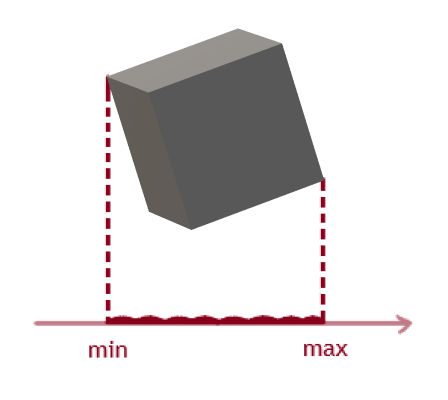
بعد ذلك ، نقوم بإنشاء دالة تُرجع نقاط الإسقاط لكل مكعب. يستغرق معلمتين للرجوع ، مصفوفة قمة ومحور فاصل محتمل.

private static void ProjAxis(out float min, out float max, Vector3[] points, Vector3 Axis)
{
        max = ProjVector3(points[0], Axis);
        min = ProjVector3(points[0], Axis);
        for (int i = 1; i < points.Length; i++)
        {
            float tmp = ProjVector3(points[i], Axis);
            if (tmp > max)
            {
                max = tmp;
            }

            if (tmp < min)
            {
                min= tmp;
            }
        }
}

لذا ، بتطبيق هذه الوظيفة ( ProjAxis ) ، نحصل على نقاط الإسقاط لكل مكعب.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
            //  a
            float max_a;
            float min_a;
            ProjAxis(out min_a,out max_a,a,Axis[j]);

            //  b
            float max_b;
            float min_b;
            ProjAxis(out min_b,out max_b,b,Axis[j]);
            
            //...
        }
        //...
}

بعد ذلك ، استنادًا إلى رؤوس الإسقاط ، نحدد تقاطع الإسقاطات:

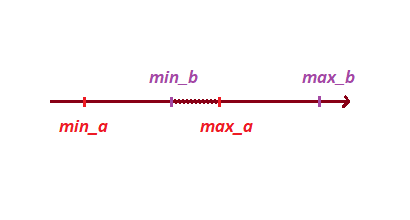
للقيام بذلك ، دعنا نضع نقاطنا في مصفوفة ونفرزها ، ستساعدنا هذه الطريقة على تحديد ليس فقط التقاطع ، ولكن أيضًا عمق التقاطع.

            float[] points = {min_a, max_a, min_b, max_b};
            Array.Sort(points);

لاحظ الخاصية التالية:

1) إذا لم تتقاطع المقاطع ، فسيكون مجموع المقاطع أقل من المقطع من خلال النقاط المتطرفة المشكلة:

2) إذا تقاطع المقاطع ، فسيكون مجموع المقاطع أكبر من المقطع من خلال النقاط المتطرفة التي تم تكوينها:

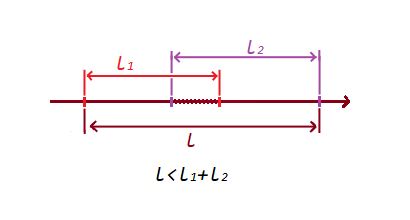
مع هذا الشرط البسيط ، قمنا بفحص التقاطع وعدم التقاطع شرائح.

إذا لم يكن هناك تقاطع ، فسيكون عمق التقاطع صفرًا:

            //...
            // 
            float sum = (max_b - min_b) + (max_a - min_a);
            //  
            float len = Math.Abs(p[3] - p[0]);
            
            if (sum <= len)
            {
                //  
                //  
                return Vector3.zero;
            }
            //,        
            //....

وبالتالي ، يكفي أن يكون لدينا متجه واحد على الأقل لا تتقاطع فيه إسقاطات المكعبات ، ثم لا تتقاطع المكعبات نفسها. لذلك ، عندما نجد محور التقسيم ، يمكننا تخطي التحقق من المتجهات المتبقية وإنهاء الخوارزمية.

في حالة تقاطع المكعبات ، كل شيء أكثر إثارة للاهتمام: سيتقاطع إسقاط المكعبات على جميع المتجهات ، ويجب أن نحدد المتجه بأقل تقاطع.

لنقم بإنشاء هذا المتجه قبل الحلقة ، وسوف نقوم بتخزين المتجه مع الحد الأدنى للطول فيه. وهكذا ، في نهاية الدورة ، نحصل على المتجه المطلوب.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        Vector3 norm = new Vector3(10000,10000,10000);
        for (int j = 0; j < Axis.Count; j++)
        {
                //...
        }
        // ,      ,  
        return norm;
{

وفي كل مرة نجد فيها المحور الذي تتقاطع فيه الإسقاطات ، نتحقق مما إذا كان أصغر طول بين الجميع. نضرب مثل هذا المحور في طول التقاطع ، وستكون النتيجة هي (الاتجاه) الطبيعي المطلوب لتقاطع المكعبات.

أضفت أيضًا تعريفًا لاتجاه الطبيعي فيما يتعلق بالمكعب الأول.

//...
if (sum <= len)
{
   //  
   //   
   return new Vector3(0,0,0);
}
//,        

//  -    2  1    
//(.       )
float dl = Math.Abs(points[2] - points[1]);
if (dl < norm.magnitude)
{
   norm = Axis[j] * dl;
   // 
   if(points[0] != min_a)
   norm = -norm;
}
//...

الكود كله

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List<Vector3> Axis)
{
        Vector3 norm = new Vector3(10000,10000,10000);
        for (int j = 0; j < Axis.Count; j++)
        {
            //  a
            float max_a;
            float min_a;
            ProjAxis(out min_a,out max_a,a,Axis[j]);

            //  b
            float max_b;
            float min_b;
            ProjAxis(out min_b,out max_b,b,Axis[j]);

            float[] points = {min_a, max_a, min_b, max_b};
            Array.Sort(points);

            float sum = (max_b - min_b) + (max_a - min_a);
            float len = Math.Abs(points[3] - points[0]);
            
            if (sum <= len)
            {
                //  
                //   
                return new Vector3(0,0,0);
            }
            float dl = Math.Abs(points[2] - points[1]);
            if (dl < norm.magnitude)
            {
                norm = Axis[j] * dl;

                // 
                if(points[0] != min_a)
                    norm = -norm;
            }

        }
        return norm;
}

خاتمة

يتم تحميل المشروع مع التنفيذ والمثال على GitHub ، ويمكنك مشاهدته هنا .

كان هدفي هو مشاركة تجربتي في حل المشكلات المتعلقة بتحديد تقاطعات شيئين محددين. ومن الممكن أيضًا فهمها عن هذه النظرية ويمكن فهمها.

كشف التصادم ونظرية محور التقسيم