
مرحباً بالجميع ، اليوم سنتعامل مع خوارزمية ضغط JPEG. كثير من الناس لا يعرفون أن JPEG ليس تنسيقًا بقدر ما هو خوارزمية. معظم صور JPEG التي تراها موجودة بتنسيق JFIF (تنسيق تبادل ملف JPEG) ، حيث يتم تطبيق خوارزمية ضغط JPEG. بنهاية المقال ، سيكون لديك فهم أفضل لكيفية ضغط هذه الخوارزمية للبيانات وكيفية كتابة كود التفريغ في بايثون. لن نأخذ في الاعتبار جميع الفروق الدقيقة في تنسيق JPEG (على سبيل المثال ، المسح التدريجي) ، لكننا سنتحدث فقط عن الإمكانات الأساسية للتنسيق أثناء كتابة وحدة فك التشفير الخاصة بنا.
المقدمة
لماذا تكتب مقالة أخرى على JPEG في حين أن مئات المقالات قد كتبت عنها بالفعل؟ عادة ، في مثل هذه المقالات ، يتحدث المؤلفون فقط عن الشكل. أنت لا تكتب كود التفريغ وفك التشفير. وحتى إذا كتبت شيئًا ما ، فسيكون في C / C ++ ، ولن يكون هذا الرمز متاحًا لمجموعة كبيرة من الأشخاص. أريد كسر هذا التقليد وإظهار كيفية عمل وحدة فك ترميز JPEG الأساسية باستخدام Python 3. سيعتمد على هذا الكود الذي طوره معهد ماساتشوستس للتكنولوجيا ، لكنني سأغيره كثيرًا من أجل سهولة القراءة والوضوح. يمكنك العثور على الكود المعدل لهذه المقالة في مستودعي .
أجزاء مختلفة من JPEG
لنبدأ بصورة أنجي ألبرتيني . يسرد جميع أجزاء ملف JPEG بسيط. سنقوم بتحليل كل جزء ، وبينما تقرأ المقال ستعود إلى هذا الرسم التوضيحي أكثر من مرة.
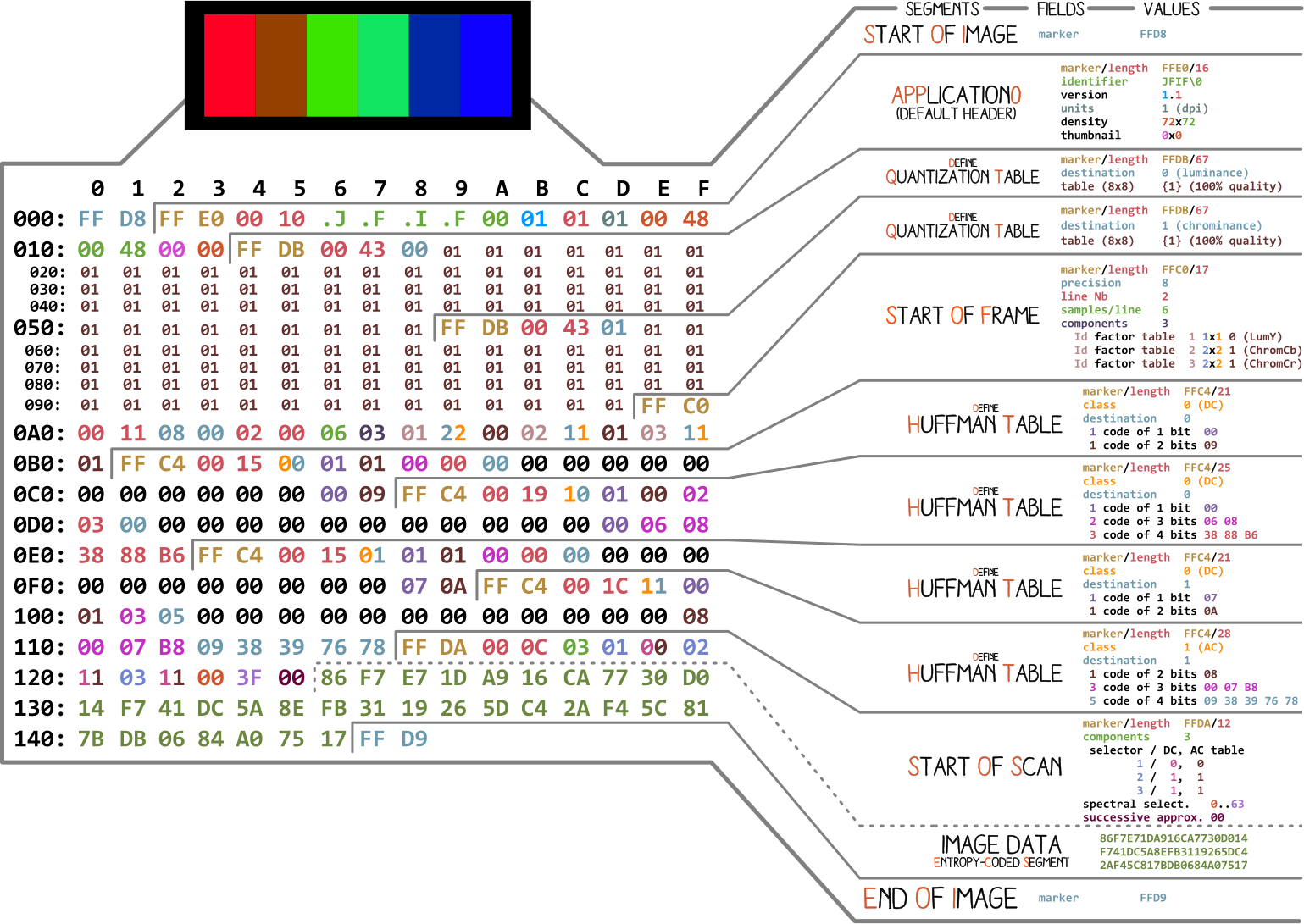
يحتوي كل ملف ثنائي تقريبًا على عدة علامات (أو رؤوس). يمكنك التفكير فيها كنوع من الإشارات المرجعية. إنها ضرورية للعمل مع الملف وتستخدمها برامج مثل الملف (في نظامي Mac و Linux) حتى نتمكن من معرفة تفاصيل الملف. تشير العلامات بالضبط إلى مكان تخزين معلومات معينة في الملف. في أغلب الأحيان ، يتم وضع العلامات وفقًا لطول (
length) مقطع معين.
بداية ونهاية الملف
أول علامة مهمة بالنسبة لنا هي
FF D8. يحدد بداية الصورة. إذا لم نعثر عليه ، فيمكننا أن نفترض أن العلامة موجودة في ملف آخر. العلامة لا تقل أهمية FF D9. تقول أننا وصلنا إلى نهاية ملف الصورة. بعد كل علامة، باستثناء مجموعة FFD0- FFD9و FF01، وعلى الفور تأتي قيمة طول جزء من هذه العلامة. وتكون علامات بداية الملف ونهايته دائمًا بطول 2 بايت.
سنعمل مع هذه الصورة:

دعنا نكتب بعض التعليمات البرمجية للعثور على علامات البداية والنهاية.
from struct import unpack
marker_mapping = {
0xffd8: "Start of Image",
0xffe0: "Application Default Header",
0xffdb: "Quantization Table",
0xffc0: "Start of Frame",
0xffc4: "Define Huffman Table",
0xffda: "Start of Scan",
0xffd9: "End of Image"
}
class JPEG:
def __init__(self, image_file):
with open(image_file, 'rb') as f:
self.img_data = f.read()
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
elif marker == 0xffda:
data = data[-2:]
else:
lenchunk, = unpack(">H", data[2:4])
data = data[2+lenchunk:]
if len(data)==0:
break
if __name__ == "__main__":
img = JPEG('profile.jpg')
img.decode()
# OUTPUT:
# Start of Image
# Application Default Header
# Quantization Table
# Quantization Table
# Start of Frame
# Huffman Table
# Huffman Table
# Huffman Table
# Huffman Table
# Start of Scan
# End of Image
لفك حزم بايت الصورة ، استخدمنا هيكل .
>Hيخبرها structبقراءة نوع البيانات unsigned shortوالعمل معها بالترتيب من الأعلى إلى الأدنى (كبير النهاية). يتم تخزين بيانات JPEG بتنسيق من الأعلى إلى الأقل. يمكن أن تكون بيانات EXIF فقط بتنسيق صغير (على الرغم من أن هذا ليس هو الحال عادة). والحجم shortهو 2 ، لذلك ننقل unpack2 بايت من img_data. كيف عرفنا ما هو short؟ ونحن نعلم أن علامات هي في JPEG يتم الرمز بأربعة أحرف عشري: ffd8. أحد هذه الأحرف يعادل أربعة بت (نصف بايت) ، لذا فإن أربعة أحرف ستعادل اثنين بايت ، تمامًا مثل short.
بعد قسم بدء المسح ، تتبع بيانات الصورة الممسوحة ضوئيًا على الفور ، والتي ليس لها طول محدد. يستمرون حتى نهاية علامة الملف ، لذلك بينما نقوم "بالبحث" يدويًا عنها عندما نجد علامة بدء المسح الضوئي.
الآن دعنا نتعامل مع بقية بيانات الصورة. للقيام بذلك ، نقوم أولاً بدراسة النظرية ، ثم ننتقل إلى البرمجة.
ترميز JPEG
أولاً ، لنتحدث عن المفاهيم الأساسية وتقنيات التشفير المستخدمة في JPEG. وسيتم إجراء الترميز بترتيب عكسي. من واقع خبرتي ، سيكون من الصعب معرفة فك التشفير بدونه.
الرسم التوضيحي أدناه ليس واضحًا لك بعد ، لكنني سأقدم لك تلميحات أثناء تعلمك لعملية التشفير وفك التشفير. فيما يلي خطوات تشفير JPEG ( المصدر ):
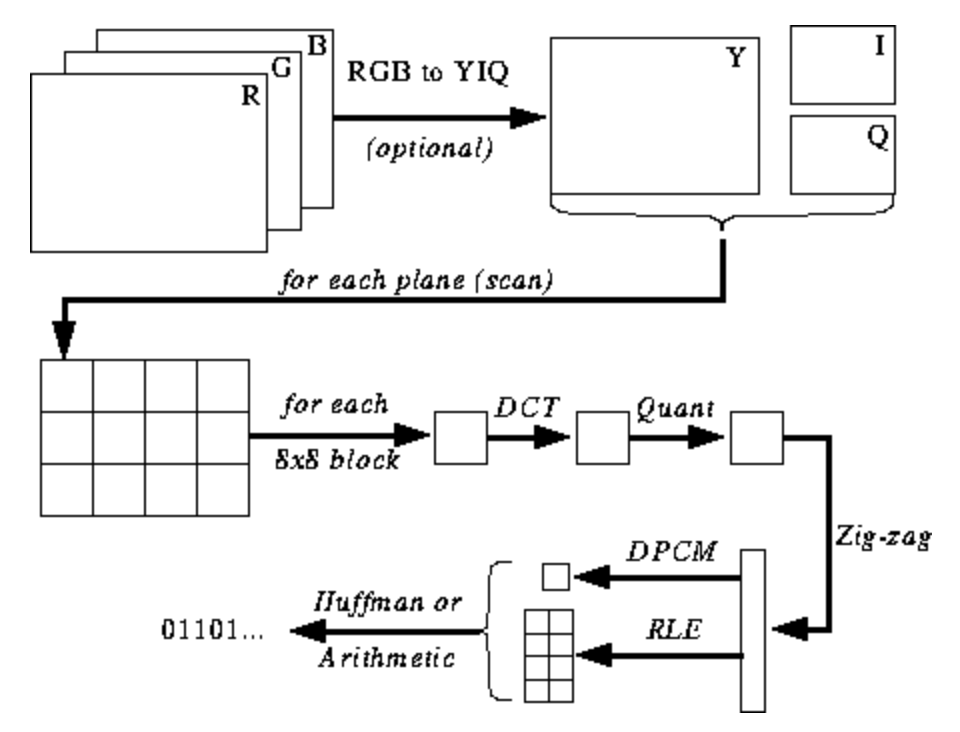
مساحة ألوان JPEG
وفقًا لمواصفات JPEG ( ISO / IEC 10918-6: 2013 (E) القسم 6.1):
- يتم التعامل مع الصور المشفرة بمكون واحد فقط كبيانات ذات تدرج رمادي ، حيث يكون 0 أسود و 255 أبيض.
- تعتبر الصور المشفرة بثلاثة مكونات بيانات RGB مشفرة في مساحة YCbCr. إذا كانت الصورة تحتوي على مقطع علامة APP14 الموضح في القسم 6.5.3 ، فسيتم اعتبار الترميز اللوني RGB أو YCbCr وفقًا للمعلومات الموجودة في مقطع علامة APP14. يتم تحديد العلاقة بين RGB و YCbCr وفقًا لمعيار ITU-T T.871 | ISO / IEC 10918-5.
- , , CMYK-, (0,0,0,0) . APP14, 6.5.3, CMYK YCCK APP14. CMYK YCCK 7.
تستخدم معظم تطبيقات خوارزمية JPEG النصوع والتلوين (ترميز YUV) بدلاً من RGB. هذا مفيد جدًا لأن العين البشرية فقيرة جدًا في التمييز بين التغيرات عالية التردد في السطوع في مناطق صغيرة ، لذلك يمكنك تقليل التردد ولن يلاحظ الشخص الفرق. ماذا تعمل، أو ماذا تفعل؟ صورة مضغوطة للغاية مع تدهور جودة غير محسوس تقريبًا.
كما هو الحال في RGB ، يتم ترميز كل بكسل بثلاثة بايت من الألوان (الأحمر والأخضر والأزرق) ، لذلك في YUV ، يتم استخدام ثلاثة بايت ، ولكن معانيها مختلفة. يحدد المكون Y سطوع اللون (النصوع ، أو الإضاءة). تحدد U و V اللون (chroma): U مسؤول عن جزء اللون الأزرق ، و V - عن الجزء الأحمر.
تم تطوير هذا التنسيق في وقت لم يكن فيه التلفزيون شائعًا بعد ، وأراد المهندسون استخدام نفس تنسيق ترميز الصورة لكل من البث التلفزيوني الملون والأبيض والأسود. اقرأ المزيد عن هذا هنا .
تحويل جيب التمام المنفصل والكمية
يحول JPEG الصورة إلى كتل 8x8 من البكسل (تسمى MCUs ، الحد الأدنى لوحدة التشفير) ، ويغير نطاق قيم البكسل بحيث يكون المركز 0 ، ثم يطبق تحويل جيب التمام المنفصل على كل كتلة ويضغط النتيجة باستخدام التكميم. دعونا نرى ماذا يعني كل هذا.
تحويل جيب التمام المنفصل (DCT) هو طريقة لتحويل البيانات المنفصلة إلى مجموعات من موجات جيب التمام. يبدو تحويل الصورة إلى مجموعة من جيب التمام وكأنه تمرين عديم الجدوى للوهلة الأولى ، لكنك ستفهم السبب عندما تتعرف على الخطوات التالية. يأخذ DCT كتلة 8x8 بكسل ويخبرنا كيفية إعادة إنتاج تلك الكتلة باستخدام مصفوفة من وظائف جيب التمام 8x8. مزيد من التفاصيل هنا .
تبدو المصفوفة كما يلي:

نحن نطبق DCT بشكل منفصل على كل مكون بكسل. نتيجة لذلك ، نحصل على مصفوفة 8x8 من المعاملات ، والتي توضح مساهمة كل (من جميع 64) دالة جيب التمام في مصفوفة الإدخال 8x8. في مصفوفة معاملات DCT ، تكون القيم الأكبر عادةً في الزاوية اليسرى العليا ، وتكون أصغرها في الزاوية اليمنى السفلى. أعلى اليسار هو أدنى دالة جيب التكرار واليمين السفلي هو الأعلى.
هذا يعني أنه في معظم الصور يوجد قدر هائل من المعلومات ذات التردد المنخفض وكمية صغيرة من المعلومات عالية التردد. إذا تم تعيين قيمة 0 للمكونات اليمنى السفلية لكل مصفوفة DCT ، فإن الصورة الناتجة ستبدو كما هي بالنسبة لنا ، لأن الشخص لا يميز التغييرات عالية التردد بشكل سيئ. هذا ما سنفعله في الخطوة التالية.
لقد وجدت مقطع فيديو رائعًا حول هذا الموضوع. انظر إذا كنت لا تفهم معنى PrEP:
نعلم جميعًا أن JPEG عبارة عن خوارزمية ضغط مع فقدان البيانات. لكن حتى الآن لم نفقد أي شيء. لدينا فقط كتل مكونة من 8x8 مكونات YUV تم تحويلها إلى كتل من وظائف جيب التمام 8x8 دون فقدان المعلومات. مرحلة فقدان البيانات هي عملية التكميم.
التكميم هو العملية عندما نأخذ قيمتين من نطاق معين ونحولهما إلى قيمة منفصلة. في حالتنا ، هذا مجرد اسم خبيث لتقليل معاملات التردد الأعلى إلى 0 في مصفوفة DCT الناتجة. عند حفظ صورة باستخدام JPEG ، تسألك معظم برامج تحرير الرسومات عن مستوى الضغط الذي تريد تعيينه. هذا هو المكان الذي يحدث فيه فقدان المعلومات عالية التردد. لن تتمكن بعد الآن من إعادة إنشاء الصورة الأصلية من صورة JPEG الناتجة.
يتم استخدام مصفوفات تكميم مختلفة اعتمادًا على نسبة الضغط (حقيقة ممتعة: معظم المطورين لديهم براءات اختراع لإنشاء جدول تكميم). نقسم مصفوفة DCT لعناصر المعاملات عنصرًا على مصفوفة التكميم ، ونقرب النتائج إلى أعداد صحيحة ونحصل على المصفوفة الكمية.
لنلقي نظرة على مثال. لنفترض أن هناك مصفوفة DCT:

وهنا مصفوفة التكميم المعتادة:
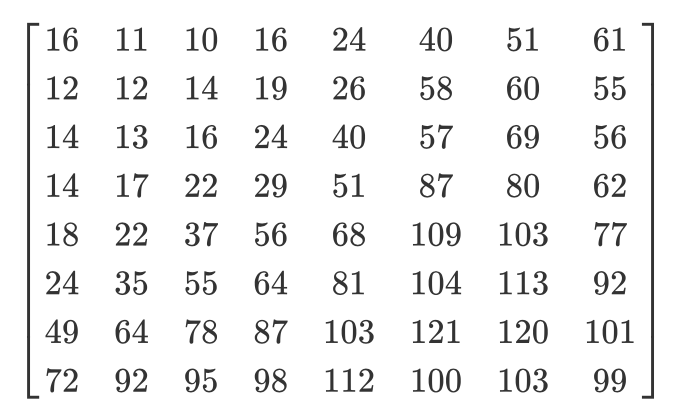
ستبدو المصفوفة الكمية كما يلي:

على الرغم من أن الإنسان لا يمكنه رؤية المعلومات عالية التردد ، إذا قمت بإزالة الكثير من البيانات من كتل 8 × 8 بكسل ، فإن الصورة ستبدو خشنة للغاية. في مثل هذه المصفوفة الكمية ، تسمى القيمة الأولى قيمة DC ، وتسمى جميع القيم الأخرى قيم AC. إذا أخذنا قيم DC لجميع المصفوفات الكمية وقمنا بإنشاء صورة جديدة ، فسنحصل على معاينة بدقة 8 مرات أصغر من الصورة الأصلية.
أريد أيضًا أن أشير إلى أنه نظرًا لأننا استخدمنا القياس ، نحتاج إلى التأكد من أن الألوان تقع في نطاق [0.255]. إذا خرجوا منه ، فسيتعين عليك إحضارهم يدويًا إلى هذا النطاق.
متعرج
بعد التكميم ، تستخدم خوارزمية JPEG مسحًا متعرجًا لتحويل المصفوفة إلى شكل أحادي البعد:
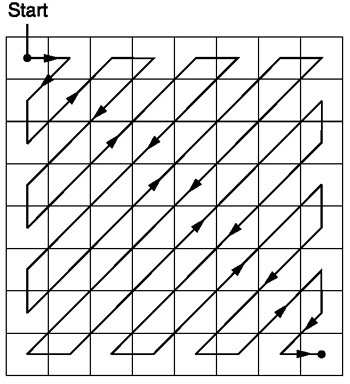
المصدر .
دعونا نحصل على مثل هذه المصفوفة الكمية:
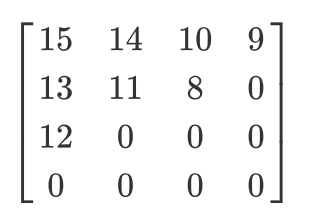
ثم تكون نتيجة المسح المتعرج كما يلي:
[15 14 13 12 11 10 9 8 0 ... 0]
يُفضل هذا الترميز لأنه بعد التكميم ، ستكون معظم المعلومات منخفضة التردد (الأكثر أهمية) موجودة في بداية المصفوفة ، ويقوم المسح المتعرج بتخزين هذه البيانات في بداية المصفوفة أحادية البعد. هذا مفيد للخطوة التالية ، الضغط.
ترميز طول التشغيل وترميز دلتا
يتم استخدام ترميز طول التشغيل لضغط البيانات المتكررة. بعد المسح المتعرج ، نرى أن هناك في الغالب أصفار في نهاية المصفوفة. يسمح لنا ترميز الطول بالاستفادة من هذه المساحة الضائعة واستخدام عدد أقل من وحدات البايت لتمثيل كل هذه الأصفار. لنفترض أن لدينا البيانات التالية:
10 10 10 10 10 10 10
بعد ترميز أطوال السلسلة ، نحصل على هذا:
7 10
لقد قمنا بضغط 7 بايت في 2 بايت.
يستخدم ترميز دلتا لتمثيل بايت بالنسبة للبايت قبله. سيكون من الأسهل الشرح بمثال. دعونا نحصل على البيانات التالية:
10 11 12 13 10 9
باستخدام ترميز دلتا ، يمكن تمثيلها على النحو التالي:
10 1 2 3 0 -1
في JPEG ، يتم ترميز كل قيمة DC لمصفوفة DCT بالنسبة إلى قيمة DC السابقة. هذا يعني أنه من خلال تغيير أول معامل DCT للصورة ، سوف تدمر الصورة بأكملها. ولكن إذا قمت بتغيير القيمة الأولى لمصفوفة DCT الأخيرة ، فلن تؤثر إلا على جزء صغير جدًا من الصورة.
هذا النهج مفيد لأن قيمة DC الأولى للصورة تميل إلى التباين أكثر من غيرها ، ومع ترميز دلتا ، فإننا نجعل باقي قيم DC أقرب إلى 0 ، مما يحسن الضغط باستخدام ترميز Huffman.
ترميز هوفمان
إنها طريقة ضغط بدون فقد. تساءل هوفمان ذات مرة ، "ما هو أصغر عدد من البتات يمكنني استخدامها لتخزين نص حر؟" نتيجة لذلك ، تم إنشاء تنسيق ترميز. لنفترض أن لدينا نصًا:
a b c d e
عادةً ما يأخذ كل حرف بايتًا واحدًا من المساحة:
a: 01100001
b: 01100010
c: 01100011
d: 01100100
e: 01100101
هذا هو مبدأ تشفير ASCII الثنائي. ماذا لو قمنا بتغيير الخرائط؟
# Mapping
000: 01100001
001: 01100010
010: 01100011
100: 01100100
011: 01100101
نحتاج الآن إلى وحدات بت أقل لتخزين نفس النص:
a: 000
b: 001
c: 010
d: 100
e: 011
كل هذا جيد وجيد ، ولكن ماذا لو احتجنا لتوفير مساحة أكبر؟ على سبيل المثال ، مثل هذا:
# Mapping
0: 01100001
1: 01100010
00: 01100011
01: 01100100
10: 01100101
a: 0
b: 1
c: 00
d: 01
e: 10
يسمح ترميز هوفمان بمثل هذه المطابقة المتغيرة الطول. يتم أخذ بيانات الإدخال ، ويتم مطابقة الأحرف الأكثر شيوعًا مع مجموعة أصغر من البتات ، وأحرف أقل تكرارًا - مع مجموعات أكبر. ثم يتم جمع التعيينات الناتجة في شجرة ثنائية. في JPEG ، نقوم بتخزين معلومات DCT باستخدام ترميز Huffman. تذكر أنني ذكرت أن قيم دلتا لترميز DC تجعل ترميز هوفمان أسهل؟ أتمنى أن تفهم الآن لماذا. بعد تشفير دلتا ، نحتاج إلى مطابقة عدد أقل من "الأحرف" وتقليل حجم الشجرة.
توم سكوت لديه مقطع فيديو رائع يشرح كيفية عمل خوارزمية هوفمان. الق نظرة قبل القراءة.
يحتوي ملف JPEG على ما يصل إلى أربعة جداول Huffman ، والتي يتم تخزينها في قسم "Define Huffman Table" (يبدأ بـ
0xffc4). يتم تخزين معاملات DCT في جدولين مختلفين من Huffman: في قيم DC واحدة من جداول متعرجة ، في الآخر - قيم AC من جداول متعرجة. هذا يعني أنه عند البرمجة ، نحتاج إلى دمج قيم DC و AC من المصفوفتين. يتم تخزين معلومات DCT لقنوات الإضاءة واللونية بشكل منفصل ، لذلك لدينا مجموعتان من DC ومجموعتان من معلومات التيار المتردد ، بإجمالي 4 جداول Huffman.
إذا كانت الصورة بتدرج الرمادي ، فلدينا جدولين فقط من Huffman (أحدهما للتيار المستمر والآخر للتيار المتردد) ، لأننا لسنا بحاجة إلى الألوان. كما قد تكون اكتشفت ، يمكن أن تحتوي صورتان مختلفتان على جداول Huffman مختلفة تمامًا ، لذلك من المهم تخزينها داخل كل JPEG.
نحن نعرف الآن المحتوى الرئيسي لصور JPEG. دعنا ننتقل إلى فك التشفير.
فك JPEG
يمكن تقسيم فك التشفير إلى مراحل:
- استخراج جداول هوفمان وفك تشفير البتات.
- استخراج معاملات DCT باستخدام التراجع عن ترميز الدلتا وطول التشغيل.
- استخدام معاملات DCT لدمج موجات جيب التمام وإعادة بناء قيم البكسل لكل كتلة 8x8.
- قم بتحويل YCbCr إلى RGB لكل بكسل.
- يعرض صورة RGB الناتجة.
يدعم معيار JPEG أربعة تنسيقات للضغط:
- يتمركز
- المسلسل الموسع
- تدريجي
- لا خسارة
سنعمل مع الضغط الأساسي. يحتوي على سلسلة من الكتل 8x8 تتبع بعضها البعض. في التنسيقات الأخرى ، يختلف قالب البيانات قليلاً. لتوضيح ذلك ، لقد قمت بتلوين أجزاء مختلفة من المحتوى السداسي العشري لصورتنا:
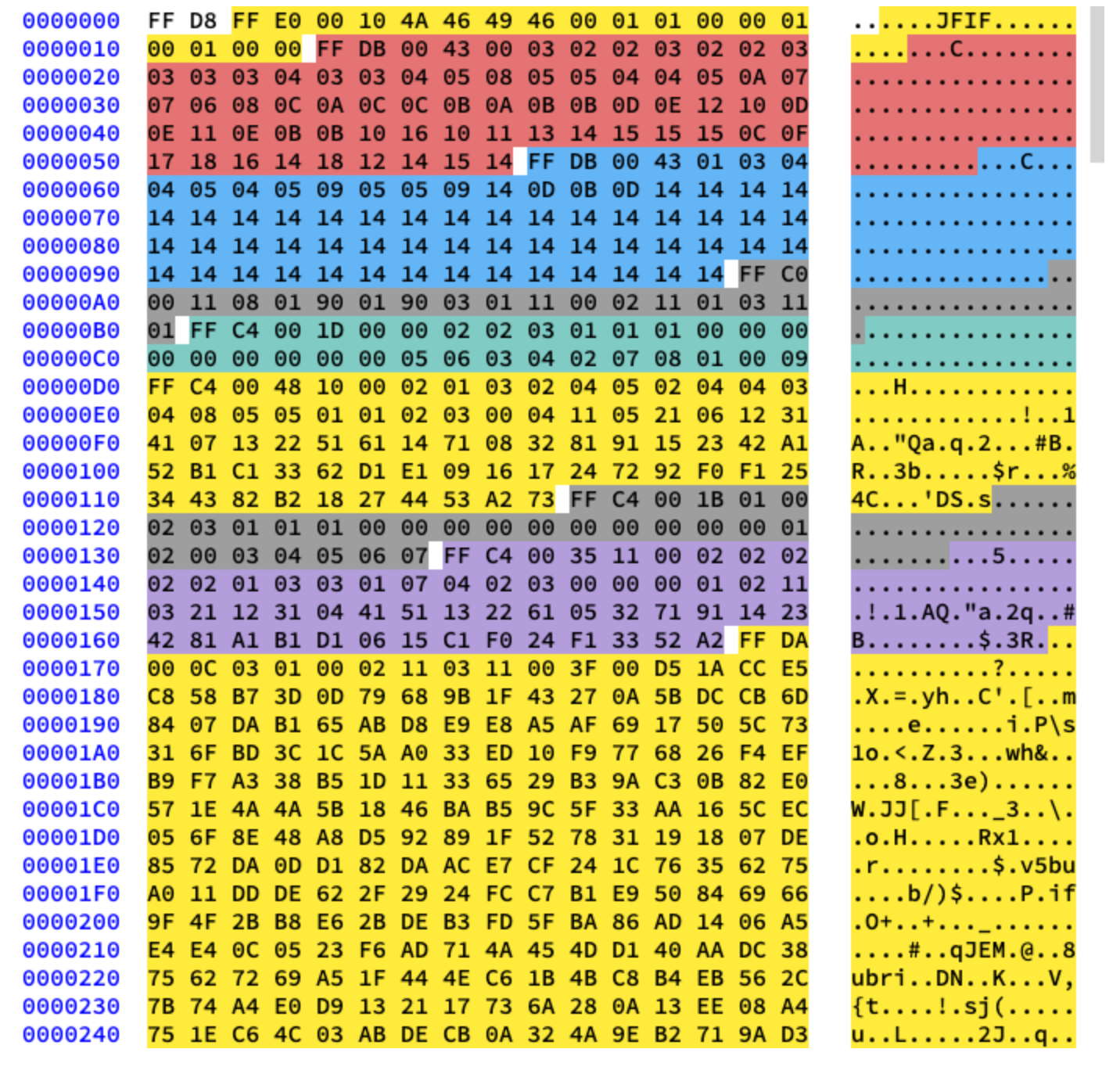
استخراج جداول هوفمان
نحن نعلم بالفعل أن JPEG يحتوي على أربعة جداول Huffman. هذا هو آخر تشفير ، لذلك سنبدأ في فك التشفير به. يحتوي كل قسم مع الجدول على معلومات:
| حقل | الحجم | وصف |
|---|---|---|
| معرف العلامة | 2 بايت | يحدد كل من 0xff و 0xc4 DHT |
| الطول | 2 بايت | طول الجدول |
| معلومات جدول هوفمان | 1 بايت | بت 0 ... 3: عدد الجداول (0 ... 3 ، وإلا خطأ) بت 4: نوع الجدول ، 0 = جدول DC ، 1 = جداول AC بت 5 ... 7: غير مستخدم ، يجب أن يكون 0 |
| الشخصيات | 16 بايت | عدد الأحرف ذات الرموز ذات الطول 1 ... 16 ، مجموع (ن) من هذه البايتات هو العدد الإجمالي للرموز التي يجب أن تكون <= 256 |
| حرف او رمز | ن بايت | يحتوي الجدول على أحرف من أجل زيادة طول الكود (ن = العدد الإجمالي للرموز). |
لنفترض أن لدينا جدول Huffman مثل هذا ( المصدر ):
| رمز | كود هوفمان | طول الكود |
|---|---|---|
| أ | 00 | 2 |
| ب | 010 | 3 |
| ج | 011 | 3 |
| د | 100 | 3 |
| ه | 101 | 3 |
| F | 110 | 3 |
| ز | 1110 | 4 |
| ح | 11110 | خمسة |
| أنا | 111110 | 6 |
| ي | 1111110 | 7 |
| ك | 11111110 | 8 |
| ل | 111111110 | تسع |
سيتم تخزينه في ملف JFIF مثل هذا (بتنسيق ثنائي. أنا أستخدم ASCII للتوضيح فقط):
0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 a b c d e f g h i j k l
0 يعني أنه ليس لدينا كود هوفمان للطول 1. يعني 1 أن لدينا كود هوفمان واحدًا للطول 2 ، وهكذا. في قسم DHT ، مباشرة بعد الفئة والمعرف ، يكون طول البيانات دائمًا 16 بايت. دعونا نكتب الكود لاستخراج الأطوال والعناصر من DHT.
class JPEG:
# ...
def decodeHuffman(self, data):
offset = 0
header, = unpack("B",data[offset:offset+1])
offset += 1
# Extract the 16 bytes containing length data
lengths = unpack("BBBBBBBBBBBBBBBB", data[offset:offset+16])
offset += 16
# Extract the elements after the initial 16 bytes
elements = []
for i in lengths:
elements += (unpack("B"*i, data[offset:offset+i]))
offset += i
print("Header: ",header)
print("lengths: ", lengths)
print("Elements: ", len(elements))
data = data[offset:]
def decode(self):
data = self.img_data
while(True):
# ---
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
data = data[len_chunk:]
if len(data)==0:
break
بعد تنفيذ الكود ، حصلنا على هذا:
Start of Image
Application Default Header
Quantization Table
Quantization Table
Start of Frame
Huffman Table
Header: 0
lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 10
Huffman Table
Header: 16
lengths: (0, 2, 1, 3, 2, 4, 5, 2, 4, 4, 3, 4, 8, 5, 5, 1)
Elements: 53
Huffman Table
Header: 1
lengths: (0, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: 8
Huffman Table
Header: 17
lengths: (0, 2, 2, 2, 2, 2, 1, 3, 3, 1, 7, 4, 2, 3, 0, 0)
Elements: 34
Start of Scan
End of Image
ممتاز! لدينا أطوال وعناصر. أنت الآن بحاجة إلى إنشاء فئة جدول Huffman الخاصة بك من أجل إعادة بناء الشجرة الثنائية من الأطوال والعناصر التي تم الحصول عليها. سأقوم فقط بنسخ الكود من هنا :
class HuffmanTable:
def __init__(self):
self.root=[]
self.elements = []
def BitsFromLengths(self, root, element, pos):
if isinstance(root,list):
if pos==0:
if len(root)<2:
root.append(element)
return True
return False
for i in [0,1]:
if len(root) == i:
root.append([])
if self.BitsFromLengths(root[i], element, pos-1) == True:
return True
return False
def GetHuffmanBits(self, lengths, elements):
self.elements = elements
ii = 0
for i in range(len(lengths)):
for j in range(lengths[i]):
self.BitsFromLengths(self.root, elements[ii], i)
ii+=1
def Find(self,st):
r = self.root
while isinstance(r, list):
r=r[st.GetBit()]
return r
def GetCode(self, st):
while(True):
res = self.Find(st)
if res == 0:
return 0
elif ( res != -1):
return res
class JPEG:
# -----
def decodeHuffman(self, data):
# ----
hf = HuffmanTable()
hf.GetHuffmanBits(lengths, elements)
data = data[offset:]
GetHuffmanBitsيأخذ الأطوال والعناصر ، يكرر العناصر ويضعها في قائمة root. إنها شجرة ثنائية وتحتوي على قوائم متداخلة. يمكنك أن تقرأ على الإنترنت كيف تعمل شجرة هوفمان وكيفية إنشاء مثل هذه البنية للبيانات في بايثون. بالنسبة إلى أول DHT لدينا (من الصورة في بداية المقالة) لدينا البيانات والأطوال والعناصر التالية:
Hex Data: 00 02 02 03 01 01 01 00 00 00 00 00 00 00 00 00
Lengths: (0, 2, 2, 3, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0)
Elements: [5, 6, 3, 4, 2, 7, 8, 1, 0, 9]
بعد المكالمة ، ستحتوي
GetHuffmanBitsالقائمة rootعلى البيانات التالية:
[[5, 6], [[3, 4], [[2, 7], [8, [1, [0, [9]]]]]]]
HuffmanTableيحتوي أيضًا على طريقة GetCodeتمر عبر الشجرة وتستخدم جدول Huffman لإرجاع البتات التي تم فك تشفيرها. تستقبل الطريقة دفق بتات كمدخل - مجرد تمثيل ثنائي للبيانات. على سبيل المثال، BITSTREAM ل abcسوف يكون 011000010110001001100011. أولاً ، نقوم بتحويل كل حرف إلى كود ASCII الخاص به ، والذي نقوم بتحويله إلى ثنائي. لنقم بإنشاء فئة للمساعدة في تحويل سلسلة إلى بتات ثم عد البتات واحدة تلو الأخرى:
class Stream:
def __init__(self, data):
self.data= data
self.pos = 0
def GetBit(self):
b = self.data[self.pos >> 3]
s = 7-(self.pos & 0x7)
self.pos+=1
return (b >> s) & 1
def GetBitN(self, l):
val = 0
for i in range(l):
val = val*2 + self.GetBit()
return val
عند التهيئة ، نقدم البيانات الثنائية للفئة ثم نقرأها باستخدام
GetBitو GetBitN.
فك جدول التكميم
يحتوي قسم تحديد جدول التكميم على البيانات التالية:
| حقل | الحجم | وصف |
|---|---|---|
| معرف العلامة | 2 بايت | يحدد كل من 0xff و 0xdb قسم DQT |
| الطول | 2 بايت | طول جدول التكميم |
| معلومات التكميم | 1 بايت | بتات 0 ... 3: عدد جداول التكميم (0 ... 3 ، وإلا خطأ) بتات 4 ... 7: دقة جدول التكميم ، 0 = 8 بتات ، وإلا 16 بت |
| بايت | ن بايت | قيم جدول القياس الكمي ، ن = 64 * (الدقة + 1) |
وفقًا لمعيار JPEG ، تحتوي صورة JPEG الافتراضية على جدولين تكميم: من أجل luma و chroma. يبدأون بعلامة
0xffdb. تحتوي نتيجة الكود الخاص بنا بالفعل على اثنتين من هذه العلامات. دعنا نضيف القدرة على فك رموز جداول التكميم:
def GetArray(type,l, length):
s = ""
for i in range(length):
s =s+type
return list(unpack(s,l[:length]))
class JPEG:
# ------
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
with open(image_file, 'rb') as f:
self.img_data = f.read()
def DefineQuantizationTables(self, data):
hdr, = unpack("B",data[0:1])
self.quant[hdr] = GetArray("B", data[1:1+64],64)
data = data[65:]
def decodeHuffman(self, data):
# ------
for i in lengths:
elements += (GetArray("B", data[off:off+i], i))
offset += i
# ------
def decode(self):
# ------
while(True):
# ----
else:
# -----
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
data = data[len_chunk:]
if len(data)==0:
break
حددنا أولاً طريقة
GetArray. إنها مجرد تقنية ملائمة لفك تشفير عدد متغير من البايت من البيانات الثنائية. لقد استبدلنا أيضًا بعض التعليمات البرمجية في الطريقة decodeHuffmanللاستفادة من الوظيفة الجديدة. ثم تم تحديد الطريقة DefineQuantizationTables: تقرأ عنوان القسم بجداول التكميم ، ثم تطبق بيانات التكميم على القاموس باستخدام قيمة الرأس كمفتاح. يمكن أن تكون هذه القيمة 0 للإضاءة و 1 للون. يحتوي كل قسم مع جداول التكميم في JFIF على 64 بايت من البيانات (لمصفوفة تكمية 8x8).
إذا قمنا بإخراج مصفوفات التكميم لصورتنا ، فسنحصل على هذا:
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
3 2 2 3 2 2 3 3
3 2 2 3 2 2 3 3
3 3 4 3 3 4 5 8
5 5 4 4 5 10 7 7
6 8 12 10 12 12 11 10
11 11 13 14 18 16 13 14
17 14 11 11 16 22 16 17
19 20 21 21 21 12 15 23
24 22 20 24 18 20 21 20
فك شفرة بداية الإطار
يحتوي قسم بداية الإطار على المعلومات ( المصدر ) التالية:
| حقل | الحجم | وصف |
|---|---|---|
| معرف العلامة | 2 بايت | 0xff 0xc0 SOF |
| 2 | 8 + *3 | |
| 1 | , 8 (12 16 ). | |
| 2 | > 0 | |
| 2 | > 0 | |
| 1 | 1 = , 3 = YcbCr YIQ | |
| 3 | 3 . (1 ) (1 = Y, 2 = Cb, 3 = Cr, 4 = I, 5 = Q), (1 ) ( 0...3 , 4...7 ), (1 ). |
نحن هنا لسنا مهتمين بكل شيء. سنستخرج عرض الصورة وارتفاعها ، وكذلك عدد جداول التكميم لكل مكون. سيتم استخدام العرض والارتفاع لبدء فك عمليات المسح الفعلية للصورة من قسم بدء المسح. نظرًا لأننا سنعمل في الغالب مع صورة YCbCr ، يمكننا افتراض أنه سيكون هناك ثلاثة مكونات ، وأنواعها ستكون 1 و 2 و 3 على التوالي. دعنا نكتب الكود لفك تشفير هذه البيانات:
class JPEG:
def __init__(self, image_file):
self.huffman_tables = {}
self.quant = {}
self.quantMapping = []
with open(image_file, 'rb') as f:
self.img_data = f.read()
# ----
def BaselineDCT(self, data):
hdr, self.height, self.width, components = unpack(">BHHB",data[0:6])
print("size %ix%i" % (self.width, self.height))
for i in range(components):
id, samp, QtbId = unpack("BBB",data[6+i*3:9+i*3])
self.quantMapping.append(QtbId)
def decode(self):
# ----
while(True):
# -----
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
data = data[len_chunk:]
if len(data)==0:
break
أضفنا سمة قائمة إلى فئة JPEG وحددنا
quantMappingطريقة BaselineDCTتقوم بفك تشفير البيانات المطلوبة من قسم SOF ووضع عدد جداول التقسيم لكل مكون في القائمة quantMapping. سنستفيد من ذلك عندما نبدأ في قراءة قسم بدء المسح. هكذا تبدو صورتنا quantMapping:
Quant mapping: [0, 1, 1]
فك تشفير بدء المسح
هذا هو "لحم" صورة JPEG ، يحتوي على بيانات الصورة نفسها. لقد وصلنا إلى أهم مرحلة. يمكن اعتبار كل ما قمنا بفك تشفيره من قبل بطاقة تساعدنا في فك تشفير الصورة نفسها. يحتوي هذا القسم على الصورة نفسها (مشفرة). نقرأ القسم ونفك تشفير البيانات باستخدام البيانات التي تم فك تشفيرها بالفعل.
بدأت جميع العلامات بـ
0xff. يمكن أن تكون هذه القيمة أيضًا جزءًا من الصورة الممسوحة ضوئيًا ، ولكن إذا كانت موجودة في هذا القسم ، فسيتبعها دائمًا و 0x00. يقوم مشفر JPEG بإدراجه تلقائيًا ، وهذا ما يسمى حشو البايت. لذلك ، يجب على وحدة فك التشفير إزالة هذه 0x00. لنبدأ بطريقة فك تشفير SOS التي تحتوي على مثل هذه الوظيفة والتخلص من تلك الموجودة 0x00. في صورتنا في القسم مع الفحص لا يوجد0xffلكنها لا تزال إضافة مفيدة.
def RemoveFF00(data):
datapro = []
i = 0
while(True):
b,bnext = unpack("BB",data[i:i+2])
if (b == 0xff):
if (bnext != 0):
break
datapro.append(data[i])
i+=2
else:
datapro.append(data[i])
i+=1
return datapro,i
class JPEG:
# ----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
return lenchunk+hdrlen
def decode(self):
data = self.img_data
while(True):
marker, = unpack(">H", data[0:2])
print(marker_mapping.get(marker))
if marker == 0xffd8:
data = data[2:]
elif marker == 0xffd9:
return
else:
len_chunk, = unpack(">H", data[2:4])
len_chunk += 2
chunk = data[4:len_chunk]
if marker == 0xffc4:
self.decodeHuffman(chunk)
elif marker == 0xffdb:
self.DefineQuantizationTables(chunk)
elif marker == 0xffc0:
self.BaselineDCT(chunk)
elif marker == 0xffda:
len_chunk = self.StartOfScan(data, len_chunk)
data = data[len_chunk:]
if len(data)==0:
break
في السابق ، بحثنا يدويًا عن نهاية الملف عندما وجدنا علامة
0xffda، ولكن الآن بعد أن أصبح لدينا أداة تتيح لنا عرض الملف بالكامل بشكل منهجي ، سننقل حالة البحث عن العلامة داخل المشغل else. RemoveFF00تتعطل الوظيفة فقط عندما تجد شيئًا آخر بدلاً من 0x00بعد 0xff. تنقطع الحلقة عندما تجد الوظيفة 0xffd9، حتى نتمكن من البحث عن نهاية الملف دون خوف من المفاجآت. إذا قمت بتشغيل هذا الرمز ، فلن ترى أي شيء جديد في المحطة.
تذكر أن JPEG يقسم الصورة إلى مصفوفات 8x8. نحتاج الآن إلى تحويل بيانات الصورة الممسوحة ضوئيًا إلى تيار بتات ومعالجتها في أجزاء 8 × 8. دعنا نضيف الكود إلى صفنا:
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk +hdrlen
لنبدأ بتحويل البيانات إلى تيار بت. هل تتذكر أن تشفير دلتا يتم تطبيقه على عنصر DC في مصفوفة التكميم (عنصرها الأول) بالنسبة إلى عنصر DC السابق؟ ولذلك، فإننا تهيئة
oldlumdccoeff، oldCbdccoeffو oldCrdccoeffمع قيم الصفر، وسوف يساعدنا على تتبع قيمة العناصر DC السابقة، و0 سيتم تعيين افتراضيا عندما نجد العنصر DC الأول. قد تبدو
الحلقة
forغريبة. self.height//8يخبرنا كم مرة يمكننا قسمة الارتفاع على 8 8 ، وهو نفس الشيء مع العرض و self.width//8.
BuildMatrixسوف يأخذ جدول تكميم ويضيف معلمات ، وينشئ مصفوفة تحويل جيب التمام المنفصل العكسي ويعطينا المصفوفات Y و Cr و Cb. وتحولهم الوظيفة DrawMatrixإلى RGB.
أولاً ، لنقم بإنشاء فصل دراسي
IDCT، ثم ابدأ في ملء الطريقة BuildMatrix.
import math
class IDCT:
"""
An inverse Discrete Cosine Transformation Class
"""
def __init__(self):
self.base = [0] * 64
self.zigzag = [
[0, 1, 5, 6, 14, 15, 27, 28],
[2, 4, 7, 13, 16, 26, 29, 42],
[3, 8, 12, 17, 25, 30, 41, 43],
[9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
]
self.idct_precision = 8
self.idct_table = [
[
(self.NormCoeff(u) * math.cos(((2.0 * x + 1.0) * u * math.pi) / 16.0))
for x in range(self.idct_precision)
]
for u in range(self.idct_precision)
]
def NormCoeff(self, n):
if n == 0:
return 1.0 / math.sqrt(2.0)
else:
return 1.0
def rearrange_using_zigzag(self):
for x in range(8):
for y in range(8):
self.zigzag[x][y] = self.base[self.zigzag[x][y]]
return self.zigzag
def perform_IDCT(self):
out = [list(range(8)) for i in range(8)]
for x in range(8):
for y in range(8):
local_sum = 0
for u in range(self.idct_precision):
for v in range(self.idct_precision):
local_sum += (
self.zigzag[v][u]
* self.idct_table[u][x]
* self.idct_table[v][y]
)
out[y][x] = local_sum // 4
self.base = out
دعنا نحلل الفصل
IDCT. عندما نستخرج MCU ، سيتم تخزينها في سمة base. ثم نقوم بتحويل مصفوفة MCU عن طريق التراجع عن المسح المتعرج باستخدام الطريقة rearrange_using_zigzag. أخيرًا ، سنعيد تحويل جيب التمام المنفصل عن طريق استدعاء الطريقة perform_IDCT.
كما تتذكر ، تم إصلاح جدول التيار المستمر. لن نفكر في كيفية عمل DCT ، فهذا أكثر ارتباطًا بالرياضيات منه بالبرمجة. يمكننا تخزين هذا الجدول كمتغير عام واستعلام عن أزواج من القيم
x,y. قررت أن أضع الجدول وحساباته في الفصل IDCTلجعل النص قابلاً للقراءة. يتم ضرب كل عنصر من عناصر مصفوفة MCU المحولة بقيمة idc_variable، ونحصل على قيم Y و Cr و Cb.
سيصبح هذا أكثر وضوحًا عند إضافة الطريقة
BuildMatrix.
إذا قمت بتعديل الجدول المتعرج ليبدو هكذا:
[[ 0, 1, 5, 6, 14, 15, 27, 28],
[ 2, 4, 7, 13, 16, 26, 29, 42],
[ 3, 8, 12, 17, 25, 30, 41, 43],
[20, 22, 33, 38, 46, 51, 55, 60],
[21, 34, 37, 47, 50, 56, 59, 61],
[35, 36, 48, 49, 57, 58, 62, 63],
[ 9, 11, 18, 24, 31, 40, 44, 53],
[10, 19, 23, 32, 39, 45, 52, 54]]
تحصل على هذه النتيجة (لاحظ القطع الأثرية الصغيرة):

وإذا كانت لديك الشجاعة ، يمكنك تعديل الجدول المتعرج أكثر:
[[12, 19, 26, 33, 40, 48, 41, 34,],
[27, 20, 13, 6, 7, 14, 21, 28,],
[ 0, 1, 8, 16, 9, 2, 3, 10,],
[17, 24, 32, 25, 18, 11, 4, 5,],
[35, 42, 49, 56, 57, 50, 43, 36,],
[29, 22, 15, 23, 30, 37, 44, 51,],
[58, 59, 52, 45, 38, 31, 39, 46,],
[53, 60, 61, 54, 47, 55, 62, 63]]
ثم ستكون النتيجة كما يلي:

لنكمل طريقتنا
BuildMatrix:
def DecodeNumber(code, bits):
l = 2**(code-1)
if bits>=l:
return bits
else:
return bits-(2*l-1)
class JPEG:
# -----
def BuildMatrix(self, st, idx, quant, olddccoeff):
i = IDCT()
code = self.huffman_tables[0 + idx].GetCode(st)
bits = st.GetBitN(code)
dccoeff = DecodeNumber(code, bits) + olddccoeff
i.base[0] = (dccoeff) * quant[0]
l = 1
while l < 64:
code = self.huffman_tables[16 + idx].GetCode(st)
if code == 0:
break
# The first part of the AC quantization table
# is the number of leading zeros
if code > 15:
l += code >> 4
code = code & 0x0F
bits = st.GetBitN(code)
if l < 64:
coeff = DecodeNumber(code, bits)
i.base[l] = coeff * quant[l]
l += 1
i.rearrange_using_zigzag()
i.perform_IDCT()
return i, dccoeff
نبدأ بإنشاء فئة انعكاس تحويل جيب التمام منفصلة (
IDCT()). ثم نقرأ البيانات في دفق البتات ونفك تشفيرها باستخدام جدول هوفمان.
self.huffman_tables[0]و self.huffman_tables[1]الرجوع إلى الجداول DC للمى وصفاء، على التوالي، و self.huffman_tables[16]و self.huffman_tables[17]الرجوع إلى جداول AC للمى وصفاء، على التوالي.
بعد فك تشفير تيار البتات ، نستخدم دالة
DecodeNumber لاستخراج معامل DC الجديد المشفر دلتا وإضافته olddccoefficientللحصول على معامل DC المشفر دلتا .
ثم نكرر نفس إجراء فك التشفير مع قيم التيار المتردد في مصفوفة التكميم. معنى الرمز
0يشير إلى أننا وصلنا إلى نهاية علامة نهاية الحظر (EOB) ويجب أن نتوقف. علاوة على ذلك ، يخبرنا الجزء الأول من جدول تكميم التيار المتردد عن عدد الأصفار البادئة التي لدينا. لنتذكر الآن كيفية ترميز أطوال المتسلسلة. دعونا نعكس هذه العملية ونتخطى كل تلك البتات العديدة. IDCTيتم تعيين أصفار لهم صراحة في الفئة .
بعد فك تشفير قيم DC و AC لـ MCU ، نقوم بتحويل MCU وعكس المسح المتعرج عن طريق الاتصال
rearrange_using_zigzag. ثم نعكس DCT ونطبقه على MCU التي تم فك تشفيرها. ستعيد
الطريقة
BuildMatrixمصفوفة DCT المقلوبة وقيمة معامل التيار المستمر. تذكر أن هذه ستكون مصفوفة لوحدة ترميز 8x8 واحدة على الأقل. لنفعل هذا لجميع MCUs الأخرى في ملفنا.
عرض صورة على الشاشة
الآن دعنا نصنع الكود الخاص بنا في الطريقة
StartOfScanلإنشاء Tkinter Canvas ونرسم كل MCU بعد فك التشفير.
def Clamp(col):
col = 255 if col>255 else col
col = 0 if col<0 else col
return int(col)
def ColorConversion(Y, Cr, Cb):
R = Cr*(2-2*.299) + Y
B = Cb*(2-2*.114) + Y
G = (Y - .114*B - .299*R)/.587
return (Clamp(R+128),Clamp(G+128),Clamp(B+128) )
def DrawMatrix(x, y, matL, matCb, matCr):
for yy in range(8):
for xx in range(8):
c = "#%02x%02x%02x" % ColorConversion(
matL[yy][xx], matCb[yy][xx], matCr[yy][xx]
)
x1, y1 = (x * 8 + xx) * 2, (y * 8 + yy) * 2
x2, y2 = (x * 8 + (xx + 1)) * 2, (y * 8 + (yy + 1)) * 2
w.create_rectangle(x1, y1, x2, y2, fill=c, outline=c)
class JPEG:
# -----
def StartOfScan(self, data, hdrlen):
data,lenchunk = RemoveFF00(data[hdrlen:])
st = Stream(data)
oldlumdccoeff, oldCbdccoeff, oldCrdccoeff = 0, 0, 0
for y in range(self.height//8):
for x in range(self.width//8):
matL, oldlumdccoeff = self.BuildMatrix(st,0, self.quant[self.quantMapping[0]], oldlumdccoeff)
matCr, oldCrdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[1]], oldCrdccoeff)
matCb, oldCbdccoeff = self.BuildMatrix(st,1, self.quant[self.quantMapping[2]], oldCbdccoeff)
DrawMatrix(x, y, matL.base, matCb.base, matCr.base )
return lenchunk+hdrlen
if __name__ == "__main__":
from tkinter import *
master = Tk()
w = Canvas(master, width=1600, height=600)
w.pack()
img = JPEG('profile.jpg')
img.decode()
mainloop()
لنبدأ بالوظائف
ColorConversionو Clamp. ColorConversionيأخذ قيم Y و Cr و Cb ، ويحولها إلى مكونات RGB بواسطة الصيغة ، ثم ينتج قيم RGB المجمعة. لماذا تضيف 128 لهم ، قد تسأل؟ تذكر ، قبل خوارزمية JPEG ، يتم تطبيق DCT على MCU وطرح 128 من قيم اللون. إذا كانت الألوان في الأصل في النطاق [0.255] ، فإن JPEG سيضعها في النطاق [-128 ، + 128]. نحتاج إلى التراجع عن هذا التأثير عند فك التشفير ، لذلك نضيف 128 إلى RGB. أما Clampعند التفريغ ، فقد تخرج القيم الناتجة عن النطاق [0.255] ، لذلك نحتفظ بها في هذا النطاق [0.255].
في الطريقة
DrawMatrixنقوم بعمل حلقة خلال كل مصفوفة 8x8 مفككة لـ Y و Cr و Cb ، ونحول كل عنصر مصفوفة إلى قيم RGB. بعد التحويل ، نرسم البكسلات في Tkinter canvasباستخدام الطريقة create_rectangle. يمكنك العثور على جميع التعليمات البرمجية على جيثب . إذا قمت بتشغيله ، سيظهر وجهي على الشاشة.
خاتمة
من كان يظن أنه لإظهار وجهي ، يجب عليك كتابة شرح لأكثر من 6000 كلمة. إنه لأمر مدهش كيف كان مؤلفو بعض الخوارزميات أذكياء! ارجو ان تكون قد استمتعت بالمقال. لقد تعلمت الكثير أثناء كتابة وحدة فك الترميز هذه. لم أكن أعتقد أن هناك الكثير من الرياضيات المتضمنة في ترميز صورة JPEG بسيطة. في المرة القادمة يمكنك محاولة كتابة وحدة فك ترميز لـ PNG (أو تنسيق آخر).
مواد إضافية
إذا كنت مهتمًا بالتفاصيل ، فاقرأ المواد التي استخدمتها لكتابة المقالة ، بالإضافة إلى بعض الأعمال الإضافية: