مقارنة طرق مختلفة لدمج قائمتين مرتبة

افترض أن لدينا قائمتين (لتبسيط الأعداد الصحيحة) ، كل منهما مرتبة. نريد دمجها في قائمة واحدة ، والتي يجب أيضًا تصنيفها. ربما تكون هذه المهمة مألوفة للجميع ؛ يتم استخدامها ، على سبيل المثال ، في دمج الفرز.

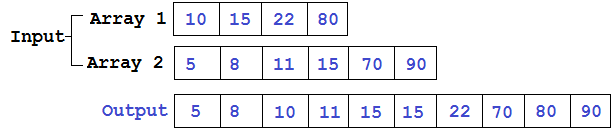
هناك العديد من طرق التنفيذ (خاصة في لغة بيثون). دعنا نلقي نظرة على بعضها ونقارن الوقت المنقضي لمدخلات مختلفة.

الفكرة الرئيسية للخوارزمية هي أنه من خلال وضع تسمية واحدة في بداية كل قائمة ، سنقارن العناصر المحددة ، ونأخذ الأصغر وننقل التسمية في قائمتها إلى الرقم التالي. عندما تنتهي إحدى القوائم ، تحتاج إلى إضافة باقي القائمة الثانية إلى النهاية.

لا تتغير بيانات الإدخال

يجب ألا تكون هناك قائمتان list1و list2.

دعونا نبدأ مع أبسط الخوارزمية: دعونا بمناسبة تسميات iو jواتخاذ أصغر واحد list1[i]، list2[j]وزيادة تسميته تلو الآخر حتى واحد من التسميات يتجاوز حدود القائمة.

أثناء المقارنة الأولى ، سنختار الحد الأدنى للعنصر من الحد الأدنى للعنصر في قائمتنا وننتقل إلى العنصر التالي ، لذلك سيكون أصغر عنصر في القائمتين في الموضع الصفري للعنصر الناتج. علاوة على ذلك ، ليس من الصعب إثبات من خلال الاستقراء أن الدمج الإضافي سوف يستمر بشكل صحيح.

دعنا ننتقل إلى الكود:

def simple_merge(list1, list2):
    i, j = 0, 0
    res = []
    while i < len(list1) and j < len(list2):
        if list1[i] < list2[j]:
            res.append(list1[i])
            i += 1
        else:
            res.append(list2[j])
            j += 1
    res += list1[i:]
    res += list2[j:] 
    #   list1[i:]  list2[j:]   ,     
    return res

لاحظ أن هذا الرمز يستخدم فقط الحركة إلى الأمام في القائمة. لذلك ، يكفي العمل مع التكرارات. دعنا نعيد كتابة الخوارزمية باستخدام التكرارات.

سنقوم أيضًا بتغيير طريقة التعامل مع نهايات القوائم ، حيث لا يمكننا الآن نسخها حتى النهاية. سنقوم بمعالجة العناصر حتى يصل كلا المتكررين إلى النهاية ، وإذا كان أحدهما في النهاية بالفعل ، فسنأخذ من الثاني.

def iter_merge(list1, list2):
    result, it1, it2 = [], iter(list1), iter(list2)
    el1 = next(it1, None)
    el2 = next(it2, None)
    while el1 is not None or el2 is not None:
        if el1 is None or (el2 is not None and el2 < el1):
            result.append(el2)
            el2 = next(it2, None)
        else:
            result.append(el1)
            el1 = next(it1, None)
    return result

(result.append()) , . , , .

def gen_merge_inner(it1, it2):
    el1 = next(it1, None)
    el2 = next(it2, None)
    while el1 is not None or el2 is not None:
        if el1 is None or (el2 is not None and el2 < el1):
            yield el2
            el2 = next(it2, None)
        else:
            yield el1
            el1 = next(it1, None)

def gen_merge(list1, list2):
    return list(gen_merge_inner(iter(list1), iter(list2))) #    

python .

• merge heapq. , , , : , , .

  
  
  

  :

  
  
  

  from heapq import merge
  
  def heapq_merge(list1, list2):
  return list(merge(list1, list2)) #   

  
  
  

• Counter collections. Counter , , , , (, ).

  
  
  

  gen_merge_inner Counter(list1) Counter(list2):

  
  
  

  def counter_merge(list1, list2):
  return list(gen_merge_inner(Counter(list1).elements(), Counter(list2).elements()))

  
  
  

• , , . .

  
  
  

  def sort_merge(list1, list2):
  return sorted(list1 + list2)

  
  
  

, ( ). . pop(0) , .

def pop_merge(list1, list2):
    result = []
    while list1 and list2:
        result.append((list1 if list1[0] < list2[0] else list2).pop(0))
    return result + list1 + list2

4 , . , , . , . , , .

def reverse_pop_merge(list1, list2):
    result = []
    while list1 and list2:
        result.append((list1 if list1[-1] > list2[-1] else list2).pop(-1))
    return (result + list1[-1::-1] + list2[-1::-1])[-1::-1]

.

, :

• simple_merge
• iter_merge
• gen_merge
• heapq_merge
• counter_merge
• sort_merge
• pop_merge
• reverse_pop_merge

timeit. .

: , , , , . .

, $$$1$ $$$10^5$, $$$1$ $$$10^6$.

pop reverse_pop:

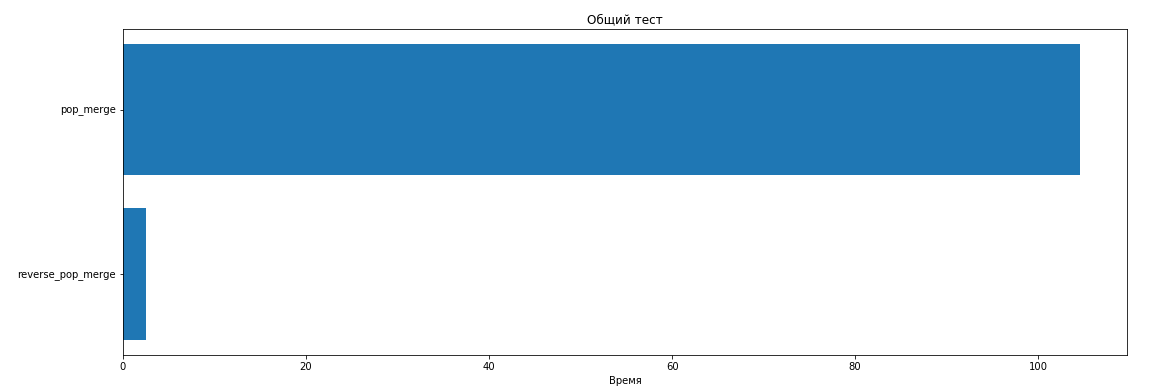
pop_merge , .

pop_merge, :

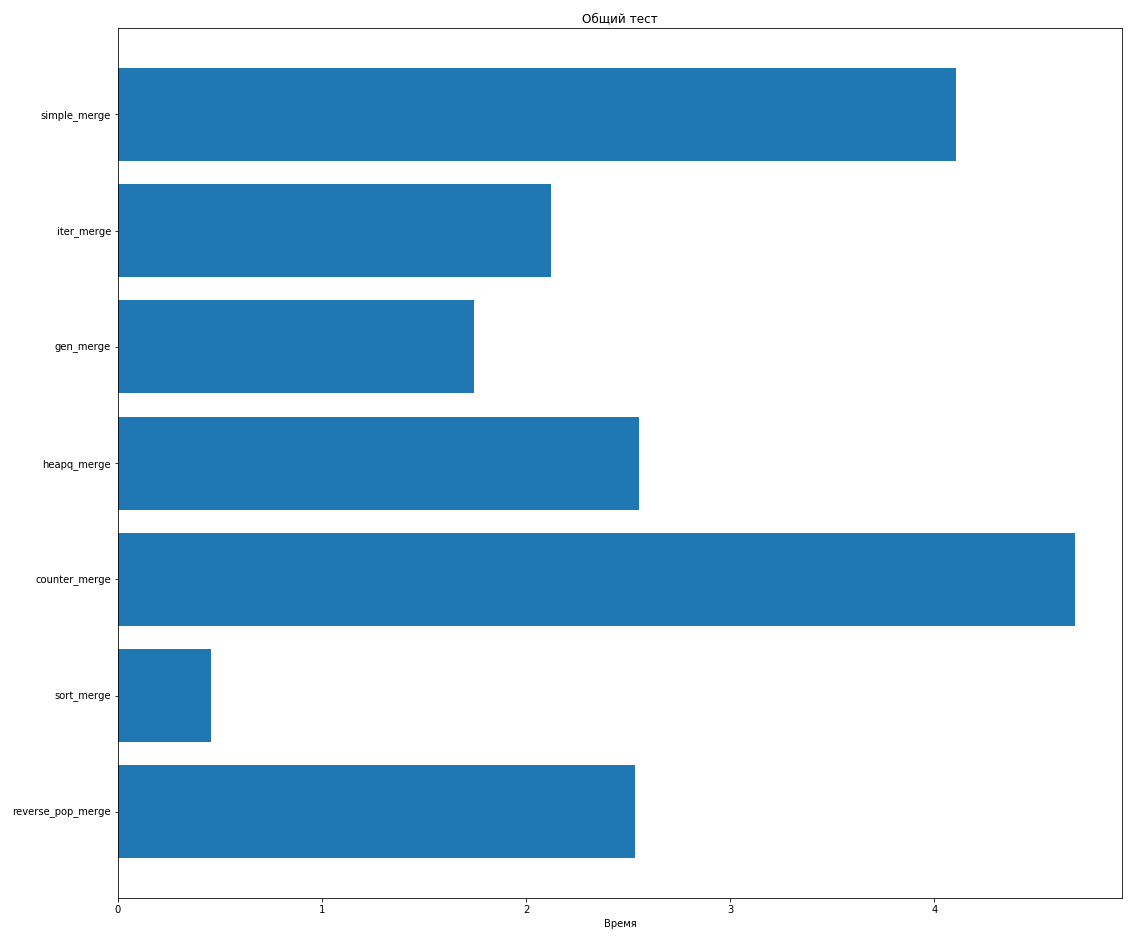
reverse_pop_merge heapq_merge.

, , , .

,

$$$[50x, 50(x+1))$, $$$x$ , $$$1$. $$$50$.

pop_merge heapq_merge, .

, ,

$$$x$, $$$10^4 + 100x$.

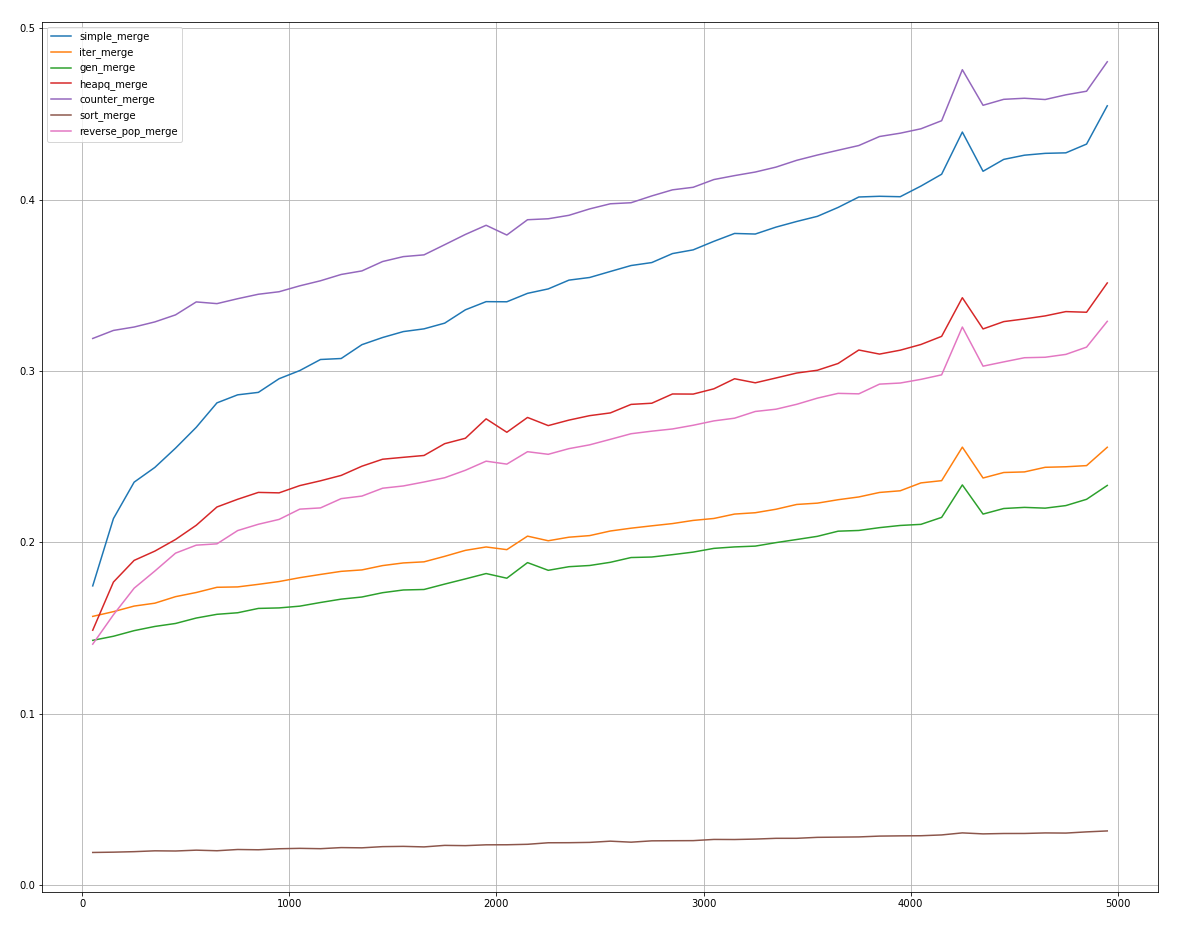
( ) reverse_pop_merge , sort_merge, .

,

, $$$5$, $$$1$.

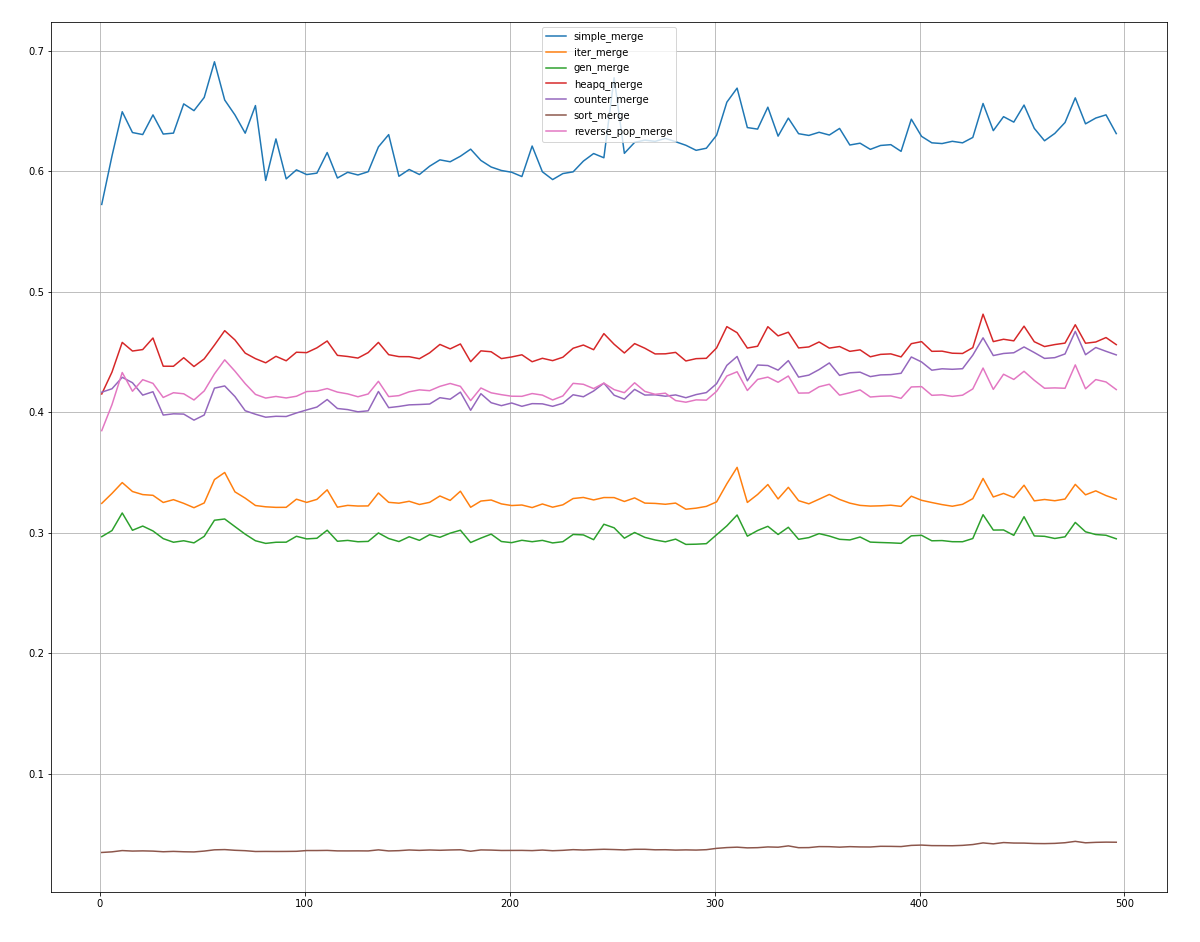
, counter_merge reverse_pop_merge heapq_merge, .

sort_merge! , .

في المرتبة الثانية ، تأتي الغالبية العظمى من الحالات gen_merge، تليها iter_merge.

تستخدم بقية الطرق وقتًا أطول ، لكن بعضها في بعض الحالات القصوى يحقق نتائج في 2-3 أماكن.

ملاحظة

يمكن العثور على الكود والاختبارات ودفتر jupyter مع الرسوم البيانية على gitlab .

ربما هذا التحليل غير مكتمل ، سأكون سعيدًا بإضافة خياراتك إلى المقارنة ، اقترح.