👮 👩‍👩‍👧 ✉️ بناء منحنى الخصم. برنامج تعليمي للمهوس ، الجزء الخامس 👆🏼 🤫 📯

دعونا نتعلم كيفية بناء منحنى الخصم. سأقول على الفور: من المهم جدًا الحصول على بيانات السوق المحدثة. إذا كنت تبحث عن مقايضات أسعار الفائدة للدولار أو اليورو أو بعض العملات الأخرى ، فلا يوجد الكثير من المعلومات المفتوحة على الإنترنت. تتوفر معظم البيانات إما من خلال محطات التداول أو من شركات خاصة - مزودي بيانات السوق. لقد عثرت على بيانات عن الكرونة الدنماركية والسويدية والنرويجية ، بالإضافة إلى بيانات لليورو والدولار على موقع إلكتروني لمجموعة مصرفية إسكندنافية كبيرة.

بعد ذلك ، سنحاول إنشاء منحنى خصم للكرونا السويدية.

هذا المنشور هو نسخة معدلة من محاضرة الفيديو الثالثة " بناء منحنى الخصم " كجزء من دورة Finmath for Fintech.

لذلك ، سيكون منحنى الخصم للكرونة لدينا هو المعدلات الليلية لكل يوم. أول شيء نعرفه هو ما يسمى بالسعر الأساسي - سعر الودائع قصيرة الأجل (القروض). علاوة على ذلك ، هناك مقايضات معروفة تتراوح من سنة إلى ثلاثين سنة. لتوضيح الطريقة ، سنرسم منحنى يصل إلى عشر سنوات. يمكن رؤية قيم بيانات السوق الحالية في هذه الصورة:

لبدء رسم المنحنى ، نحتاج إلى وضع بعض الافتراضات.

دعنا نفترض من أجل البساطة أن المقايضات الخاصة بنا هي إصلاح المقايضات المتغيرة بتواتر المدفوعات كل ستة أشهر. يوجد أدناه الرسم البياني لمقايضة سنة واحدة. نعلم أن المعدل الأساسي في البداية هو صفر بالمائة. لحساب سعر المقايضة العادل ، نحتاج إلى معرفة قيمة عامل الخصم لمدة ستة أشهر وعامل الخصم لمدة 12 شهرًا. ماذا سيكون لدينا "ساق" عائمة؟ افترض أننا سندفع متوسط القيمة الليلية لكل من النطاقات. أي أن قيمة "الضلع" العائمة تصل إلى ستة أشهر - سيكون هذا هو متوسط القيمة الليلية على مدار 180 يومًا. ستكون الضلع العائم لمدة 12 شهرًا هي نفسها ، هنا فقط سيكون هناك مجموع من اليوم 181 إلى اليوم 360.

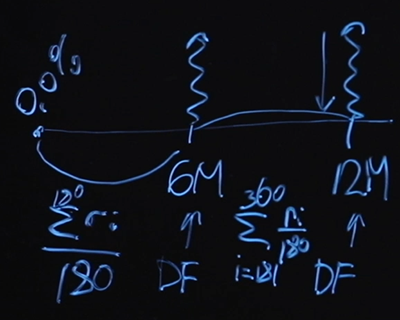
طريقة حساب المتوسط هذه معروفة على نطاق واسع. يطلق عليه مقايضة المؤشر بين عشية وضحاها ويستخدم في كثير من الأحيان في منتجات السوق. يتم تعريف الضلع العائم هنا على أنه المتوسط على مدار الفترة.

نحن نعرف السعر الأساسي وتكلفة السواب. من الواضح ، إذا كتبنا معادلة السعر العادل "وجهاً لوجه" ، فسيكون لدينا الكثير من الأشياء المجهولة. لا نعرف عامل الخصم لمدة 6 أشهر ، عامل الخصم لمدة 12 شهرًا ، ولا نعرف قيم أسعار الفائدة باستثناء واحد - الأول. الكثير من المجهول ومعادلة واحدة فقط.

ستساعدنا الفرضية التالية في حل هذه المشكلة. نحن نعرف سعر الفائدة عند النقطة صفر - هذا هو السعر الأساسي. سنفترض أن أسعار الفائدة لدينا تتغير خطيًا. دعنا نحدد X قيمة سعر الفائدة عند نقطة 12 شهرًا.

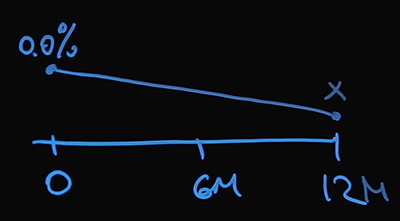
في 6 أشهر سيكون X / 2 (المتوسط الحسابي بين الصفر و X) ، ويمكننا إيجاد قيمة سعر الفائدة في أي يوم عشوائي. ولا يوجد صعوبة في حساب سعر الفائدة المتغير عند النقطتين 6 و 12 شهرًا:

\begin{array}{rcl} L_{1} & = & \frac{X}{4} \end{array}

$\begin{eqnarray} L_1&=& \frac{X}{4} \end{eqnarray}$

\begin{array}{rcl} L_{1} & = & \frac{3 X}{4} \end{array}

$\begin{eqnarray} L_1&=& \frac{3X}{4} \end{eqnarray}$

الآن دعنا ننتقل إلى عوامل الخصم. نحن نستخدم منحنى الخصم على أساس المعدل الليلي. لذلك ، فإن عامل الخصم عند نقطة ستة أشهر هو ناتج 180 عامل خصم في كل نقطة ، ومن الواضح أن هذا سيكون نوعًا من وظيفة X. يتم إنشاء

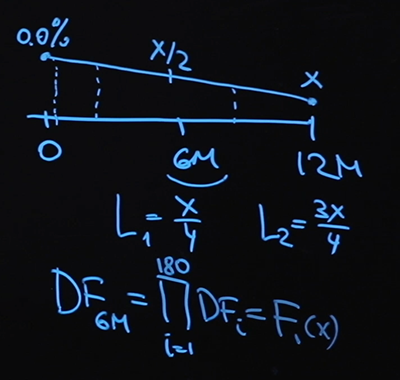
عامل الخصم عند نقطة 12 شهرًا بنفس الطريقة مع الاختلاف الوحيد الذي أحتاجه المزيد من المضاعفات. سيكون هذا أيضًا نوعًا من دالة X.

لذلك ، يتم التعبير عن عوامل الخصم من حيث X ، وهناك أيضًا القيم الأولى والثانية للمعدل العائم. دعنا ننتقل إلى كتابة المعادلة. نحن نعلم قيمة سعر المبادلة ، دعنا نقول أنها تساوي P. تذكر معادلة السعر العادل. نحتاج إلى ضرب P في عامل الخصم عند نقطة الاثني عشر شهرًا والمساواة مع المجموع التالي:

دعني أذكرك أن عامل الخصم ليوم واحد سيتم تحديده بالصيغة التالية:

\begin{array}{rcl} D F_{i} & = & \frac{1}{(1 + \frac{r_{i}}{360})} \end{array}

$\begin{eqnarray} DF_i&=& \frac{1}{(1+\frac{r_i}{360})} \end{eqnarray}$

حيث r _i هي قيمة معدل الفائدة. أستخدم الرقم 360 على افتراض أن هناك 360 يومًا في السنة (هذا اصطلاح شائع جدًا للتقويمات). في أي نقطة ، نعرف كيفية التعبير عن عامل الخصم ، r _أنا معبرًا عنه بدلالة X ، باستخدام الاستيفاء الخطي. تبين أن معادلتنا معادلة واحدة غير معروفة ، ويمكن حلها باستخدام الطرق العددية. كيفية القيام بذلك - راجع كود Python .

لذا ، فنحن نعرف كيفية إيجاد قيمة السعر عند النقطة 1 سنة. باستخدام افتراض الاستيفاء الخطي وبناءً على قيمة المقايضة التي نعرفها من السوق ، سنجد قيمة X. هنا قمنا برسم القسم الأول من المنحنى:

الآن ، لحساب سعر المبادلة لمدة عامين ، نحتاج إلى القيمة عند النقطة 6 أشهر و 12 شهرًا و 18 شهرًا وسنتين. سنستخدم بالضبط نفس الافتراض كما في المرة السابقة. دعنا نسمي قيمة السعر المطلوب Y ونستخدم أيضًا الافتراض حول خط الاستيفاء ، واستعادة القسم الثاني من المنحنى. وهكذا ، خطوة بخطوة ، سنصل إلى النهاية - إلى حد 10 سنوات.

هذه الطريقة تسمى التمهيد . إنها ليست مثالية أو هي الوحيدة الصحيحة ، ولكنها بسيطة بما يكفي للتنفيذ والفهم - طريقة التمهيد رائعة كمستوى بداية.

وجدنا منحنى الخصم. ماذا يعطينا؟ من الناحية الرسمية ، هذه هي قيم السعر الليلي في أي وقت في المستقبل حتى عشر سنوات. ربما تسأل: "من يحتاجها؟" في الواقع ، من الصعب تخيل سيناريو عندما يأتي إليك عميل ويقول: "أريد فتح وديعة ليوم واحد ، والتي ستبدأ خلال 567 يومًا". هذا موقف غير مفهوم إلى حد ما ، ولا ينبغي للمرء أن ينظر إلى المنحنى المركب في مثل هذا الشكل المباشر.

لنتخيل أن لدينا نوعًا من الدفع في المستقبل ، لنفترض سبع سنوات ونصف. سؤال: كيف نعرف قيمته الحالية؟

هذا هو بالضبط السؤال الذي سيجيب عليه منحنى الخصم. سنذهب على طول كل نقطة من المنحنى ، ونحسب عامل الخصم في كل نقطة وننهي رحلتنا عند النقطة لمدة سبع سنوات ونصف ، ونجد عامل الخصم الناتج ، ونضربه في السداد - سيكون هذا سعرًا صادقًا.

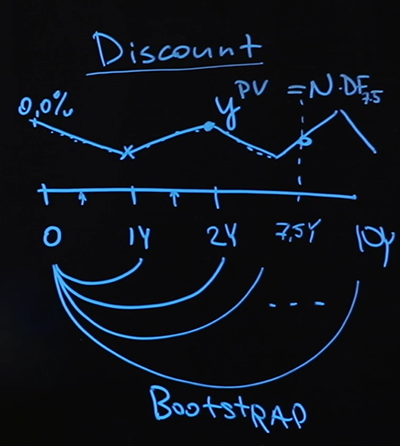
النموذج الذي استخدمته ، أي المعدلات العائمة التي أخذتها ، وكيف أقوم بتحريف القيم الوسيطة ، وبشكل عام حقيقة أنني اخترت الاستيفاء ، تم تحديده إلى حد كبير من خلال نوع البيانات التي أملكها. كان لدي القليل جدًا من البيانات - فقط معدل أساسي واحد وقيم مبادلة. إذا توفرت لي المزيد من البيانات ، أو كانت مختلفة ، فعلى الأرجح سأغير النموذج. لكن طريقة التمهيد (عندما تقوم برسم المنحنى أولاً على مقطع قصير ، ثم ترسم المزيد والمزيد ، بالاعتماد على القيم التي تم الحصول عليها مسبقًا) لا تزال سارية.

الآن دعونا نتذكر أنه بالإضافة إلى منحنيات الخصم ، نحتاج إلى منحنيات LIBOR (TIBOR ، EURIBOR ، إلخ). سيكون الاختلاف في الأدوات التي نضيفها إلى نموذجنا للحساب. سنبحث عن العقود التي تحتوي على LIBOR وبطريقة مماثلة ، باستخدام طريقة bootstrap ، سنقوم باستعادة منحنى LIBOR.

إذا كان عليك إنشاء منحنى LIBOR حقيقي ، فكن حريصًا جدًا بشأن الأدوات التي تستخدمها لبناءه ، وقم بتقييم النموذج الذي ستستخدمه بعناية. في هذه الحالة ، استخدمت الخصم بين عشية وضحاها ، ولكن هناك حاجة إلى طريقة مختلفة لإنشاء منحنى LIBOR. على الأرجح ، سيكون الخصم كل ثلاثة أشهر أو ستة ، حسب الأداة. إذا كانت لديك بيانات كافية ، يمكنك رسم منحنى LIBOR ومنحنى EURIBOR ومنحنى TIBOR وأي شيء آخر.

إذا أتى إليك عميل بالكلمات التالية: "أريد مقايضة سعر الفائدة ليس لمدة عشر سنوات ، ولكن لمدة 134 شهرًا ، حيث سأدفع ليبور معومًا كل 25 يومًا" ، فهذه ليست مشكلة. لدينا منحنى LIBOR ، نستخدم افتراض الاستيفاء ، يمكننا استعادة قيمة LIBOR في أي وقت. نحن نعلم قيمة منحنى الخصم عند كل نقطة ، ويمكننا أيضًا حساب جميع المدفوعات وإيجاد سعر "الضلع" الثابت الذي يوازن هذه المدفوعات العائمة. وبالتالي ، يمكنك العثور على قيم الأسعار العادلة لأي أداة على الإطلاق عن طريق رسم منحنيات متعددة.

لذا دعنا نتناول النقاط البارزة مرة أخرى. أخذت البيانات المتاحة وقمت ببعض الافتراضات. أولاً ، جدول الدفع: كم مرة ، وكم مرة ، يدفع كل طرف ساق ثابتة وساق عائمة. ثانيًا ، كيف سأحسب الرهان على الضلع العائم؟ الافتراض الثالث يتعلق باستيفاء الرهان الخطي. باستخدام كل هذه الافتراضات الثلاثة ، قمت بصياغة العديد من المعادلات غير الخطية ، والتي قمت بحلها عدديًا. يمكن العثور على دفتر Jupyter هنا. بالتتابع ، بدءًا من أقصر جزء في سنة واحدة ، ثم سنتان ، أو ثلاثة ، إلخ ، أعدت بناء المنحنى لفترة تصل إلى 10 سنوات. هذا هو منحنى الخصم الخاص بي الذي يمكنني استخدامه لتقييم أي أداة. تسمى هذه الطريقة bootstrap: مقطع المنحنى الذي قمت بحسابه في البداية ، أستخدمه في الخطوة الثانية ، وإلا ،ما حصلت عليه في الخطوة الثانية ، استخدمه للخطوة الثالثة وما إلى ذلك ، حتى يتشكل المنحنى بالكامل.

آمل ألا تكون الآن "تطفو" في موضوع أسعار الفائدة المتغيرة وأن تجد الفانيليا من بين أسعار الفائدة على المقايضات. ويمكنك أيضًا بناء أي منحنى باستخدام طريقة bootstrap.

جميع المقالات في هذه السلسلة

بناء منحنى الخصم. برنامج تعليمي للمهوس ، الجزء الخامس

More articles: