👩🏿‍🍳 🧝🏻 📵 Armored Warfare: مشروع Armata. انحراف لوني 🥢 🥂 📙

Armored Warfare: Project Armata هي لعبة دبابات مجانية عبر الإنترنت تم تطويرها بواسطة Allods Team ، استوديو الألعاب MY.GAMES. على الرغم من حقيقة أن اللعبة مصنوعة على CryEngine ، وهو محرك شائع إلى حد ما مع عرض جيد في الوقت الفعلي ، إلا أنه يتعين على لعبتنا تعديل وإنشاء الكثير من الصفر. في هذه المقالة ، أود أن أتحدث عن كيفية تنفيذ الانحراف اللوني من أجل رؤية الشخص الأول ، وما هو.

ما هو الانحراف اللوني؟

الانحراف اللوني هو عيب في العدسة لا تصل فيه جميع الألوان إلى نفس النقطة. هذا يرجع إلى حقيقة أن مؤشر الانكسار للوسط يعتمد على طول موجة الضوء (انظر التشتت ). على سبيل المثال ، هذه هي الطريقة التي تبدو بها الحالة عندما لا تعاني العدسة من الانحراف اللوني:

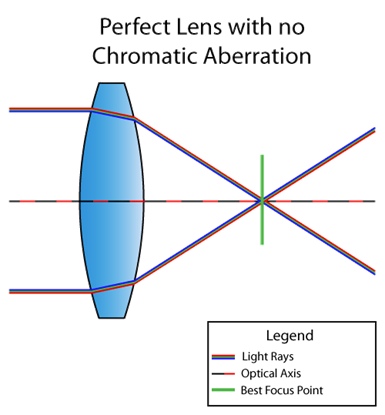
وهنا عدسة بها عيب:

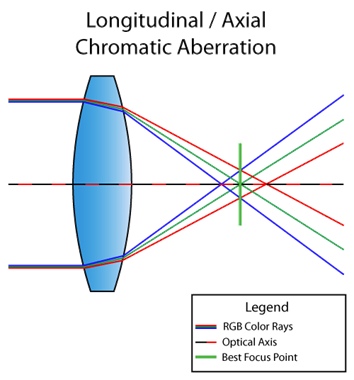
بالمناسبة ، الحالة المذكورة أعلاه تسمى الانحراف اللوني الطولي (أو المحوري). يحدث هذا عندما لا تتقارب أطوال موجية مختلفة في نفس النقطة في المستوى البؤري بعد المرور عبر العدسة. ثم يظهر الخلل في الصورة الكاملة:

في الصورة أعلاه ، يمكنك أن ترى أن الألوان الأرجواني والأخضر تبرز بسبب وجود عيب. لايمكن الرؤية؟ وفي هذه الصورة؟

هناك أيضًا انحراف لوني جانبي (أو جانبي). ويحدث ذلك عندما يقع الضوء في زاوية العدسة. ونتيجة لذلك ، تتلاقى أطوال موجية مختلفة من الضوء عند نقاط مختلفة في المستوى البؤري. هذه صورة لك لتفهمها:

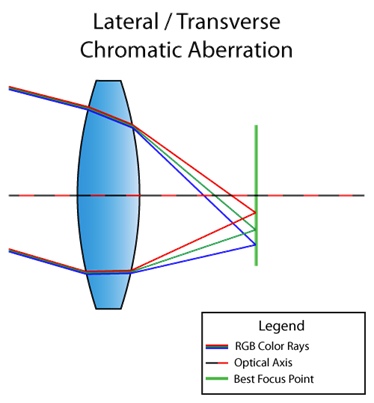
يمكنك أن ترى بالفعل من الرسم البياني أنه نتيجة لذلك نحصل على تحلل كامل للضوء من الأحمر إلى البنفسجي. على عكس الطول الطولي ، لا يظهر الزيغ اللوني الجانبي في المنتصف ، وهو أقرب إلى حواف الصورة فقط. حتى تفهم ما أعنيه ، إليك صورة أخرى من الإنترنت:

حسنًا ، بما أننا انتهينا من النظرية ، فلننتقل إلى النقطة.

الزيغ اللوني الجانبي مع التحلل الخفيف

سأبدأ بحقيقة أنني سأجيب على السؤال الذي يمكن أن يطرح في رأس العديد منكم: "أليس CryEngine ينفذ الزيغ اللوني؟" هناك. ولكن يتم استخدامه في مرحلة ما بعد المعالجة في نفس التظليل مع الشحذ ، وتبدو الخوارزمية على هذا النحو ( رابط إلى الكود ):

screenColor.r = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 + 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).r;
screenColor.b = shScreenTex.SampleLevel( shPointClampSampler, (IN.baseTC.xy - 0.5) * (1 - 2 * psParams[0].x * CV_ScreenSize.zw) + 0.5, 0.0f).b;

الذي ، من حيث المبدأ ، يعمل. لكن لدينا لعبة عن الدبابات. نحن بحاجة إلى هذا التأثير فقط من أجل رؤية الشخص الأول ، وفقط للجمال ، أي أن كل شيء يتم التركيز عليه في المركز (مرحبًا بالانحراف الجانبي). لذلك ، لم يتناسب التطبيق الحالي على الأقل مع حقيقة أن تأثيره كان مرئيًا في جميع أنحاء الصورة.

هذا هو شكل الانحراف نفسه (الانتباه إلى الجانب الأيسر):

وهذه هي الطريقة التي تبدو بها إذا قمت بتحريف المعلمات:

لذلك ، حددنا هدفنا:

تنفيذ الانحراف اللوني الجانبي بحيث يكون كل شيء في التركيز بالقرب من النطاق ، وإذا لم تكن العيوب اللونية المميزة مرئية على الجانبين ، فيجب على الأقل عدم وضوحها.
اختبر نسيجًا بضرب قنوات RGB بمعامل يتوافق مع طول موجة محدد. لم أتحدث عن هذا بعد ، لذا فقد لا يكون واضحًا تمامًا ما هي هذه النقطة. لكننا سننظر بالتأكيد في كل التفاصيل لاحقًا.

أولاً ، دعنا نلقي نظرة على الآلية العامة والرمز لإنشاء الانحراف اللوني الجانبي.

half distanceStrength = pow(length(IN.baseTC - 0.5), falloff);
half2 direction = normalize(IN.baseTC.xy - 0.5);
half2 velocity = direction * blur * distanceStrength;

لذلك ، أولاً ، يتم بناء قناع دائري ، وهو المسؤول عن المسافة من مركز الشاشة ، ثم يتم حساب الاتجاه من مركز الشاشة ، ثم يتم ضرب كل هذا blur. Blurو falloff- هذه معلمات يتم تمريرها من الخارج وهي مجرد مضاعفات لضبط الانحراف. أيضا ، يتم طرح معلمة من الخارج sampleCount، وهي ليست مسؤولة فقط عن عدد العينات ، ولكن أيضًا ، في الواقع ، عن الخطوة بين نقاط أخذ العينات ، حيث

half2 offsetDecrement = velocity * stepMultiplier / half(sampleCount);

الآن علينا فقط أن نذهب sampleCountمرة واحدة من نقطة معينة من النسيج ، ونتحول في كل مرة offsetDecrement، واضرب القنوات في أوزان الموجة المقابلة وقسمها على مجموع هذه الأوزان. حسنًا ، حان الوقت للحديث عن النقطة الثانية من هدفنا العالمي.

يتراوح الطيف المرئي للضوء من 380 نانومتر (البنفسجي) إلى 780 نانومتر (أحمر). وها ، يمكن تحويل الطول الموجي إلى لوحة RGB. في Python ، يبدو الرمز الذي يقوم بهذا السحر كما يلي:

def get_color(waveLength):
    if waveLength >= 380 and waveLength < 440:
        red = -(waveLength - 440.0) / (440.0 - 380.0)
        green = 0.0
        blue  = 1.0
    elif waveLength >= 440 and waveLength < 490:
        red   = 0.0
        green = (waveLength - 440.0) / (490.0 - 440.0)
        blue  = 1.0
    elif waveLength >= 490 and waveLength < 510:
        red   = 0.0
        green = 1.0
        blue  = -(waveLength - 510.0) / (510.0 - 490.0)
    elif waveLength >= 510 and waveLength < 580:
        red   = (waveLength - 510.0) / (580.0 - 510.0)
        green = 1.0
        blue  = 0.0
    elif waveLength >= 580 and waveLength < 645:
        red   = 1.0
        green = -(waveLength - 645.0) / (645.0 - 580.0)
        blue  = 0.0
    elif waveLength >= 645 and waveLength < 781:
        red   = 1.0
        green = 0.0
        blue  = 0.0
    else:
        red   = 0.0
        green = 0.0
        blue  = 0.0
    
    factor = 0.0
    if waveLength >= 380 and waveLength < 420:
        factor = 0.3 + 0.7*(waveLength - 380.0) / (420.0 - 380.0)
    elif waveLength >= 420 and waveLength < 701:
        factor = 1.0
    elif waveLength >= 701 and waveLength < 781:
        factor = 0.3 + 0.7*(780.0 - waveLength) / (780.0 - 700.0)
 
    gamma = 0.80
    R = (red   * factor)**gamma if red > 0 else 0
    G = (green * factor)**gamma if green > 0 else 0
    B = (blue  * factor)**gamma if blue > 0 else 0
    
    return R, G, B

ونتيجة لذلك ، نحصل على توزيع الألوان التالي:

باختصار ، يوضح الرسم البياني كم ولون ما يوجد في موجة بطول محدد. على المحور الإحداثي ، نحصل على نفس الأوزان التي تحدثت عنها سابقًا. الآن يمكننا تنفيذ الخوارزمية بالكامل ، مع مراعاة ما سبق ذكره:

half3 accumulator = (half3) 0;
half2 offset = (half2) 0;
half3 WeightSum = (half3) 0;
half3 Weight = (half3) 0;
half3 color;
half waveLength;
 
for (int i = 0; i < sampleCount; i++)
{
    waveLength = lerp(startWaveLength, endWaveLength, (half)(i) / (sampleCount - 1.0));
    Weight.r = GetRedWeight(waveLength);
    Weight.g = GetGreenWeight(waveLength);
    Weight.b = GetBlueWeight(waveLength);
        
    offset -= offsetDecrement;
        
    color = tex2Dlod(baseMap, half4(IN.baseTC + offset, 0, 0)).rgb;
    accumulator.rgb += color.rgb * Weight.rgb; 
        
    WeightSum.rgb += Weight.rgb;
}
 
OUT.Color.rgb = half4(accumulator.rgb / WeightSum.rgb, 1.0);

أي ، الفكرة هي أنه كلما كان لدينا sampleCount، كلما كانت الخطوة بين نقاط العينة أصغر ، وكلما قمنا بتفريق الضوء (نأخذ في الاعتبار المزيد من الموجات ذات الأطوال الموجية المختلفة).

إذا كان لا يزال غير واضح، ثم السماح نظرة لفي المثال محددة، وهي أول محاولة لدينا، وسوف أشرح ما لاتخاذ ل startWaveLengthو endWaveLength، وكيف سيتم تنفيذ المهام GetRed(Green, Blue)Weight.

تركيب الطيف المرئي بالكامل

لذا ، من الرسم البياني أعلاه ، نعرف النسبة التقريبية والقيم التقريبية للوحة RGB لكل طول موجة. على سبيل المثال ، لطول موجة 380 نانومتر (البنفسجي) (انظر نفس الرسم البياني) ، نرى أن RGB (0.4 ، 0 ، 0.4). هذه هي القيم التي نأخذها للأوزان التي تحدثت عنها سابقًا.

الآن دعنا نحاول التخلص من وظيفة الحصول على اللون عن طريق كثير الحدود من الدرجة الرابعة بحيث تكون الحسابات أرخص (نحن لسنا استوديو Pixar ، ولكن استوديو الألعاب: كلما كانت الحسابات أرخص ، كان ذلك أفضل). يجب أن يقترب كثير الحدود من الدرجة الرابعة من الرسوم البيانية الناتجة. لبناء كثير الحدود ، استخدمت مكتبة SciPy:

wave_arange = numpy.arange(380, 780, 0.001)
red_func = numpy.polynomial.polynomial.Polynomial.fit(wave_arange, red, 4)

ونتيجة لذلك ، يتم الحصول على النتيجة التالية (لقد قسمت إلى 3 رسوم بيانية منفصلة تقابل كل قناة منفصلة ، بحيث يكون من السهل المقارنة بالقيمة الدقيقة):

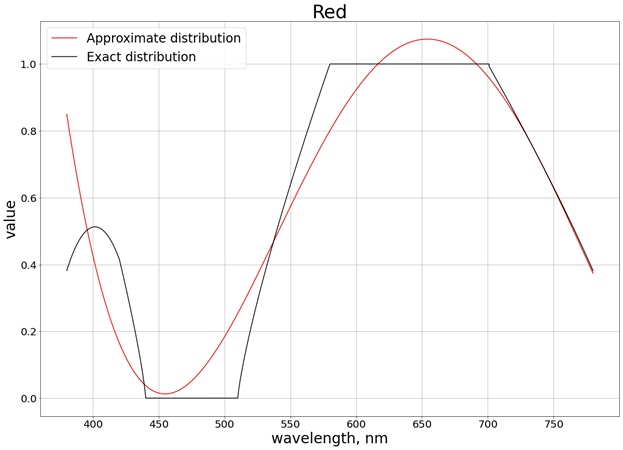
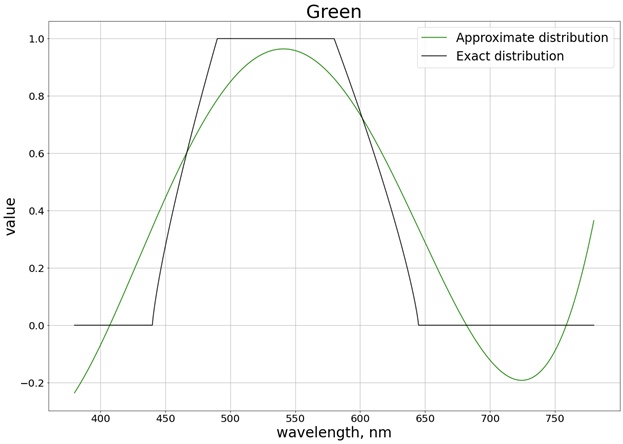
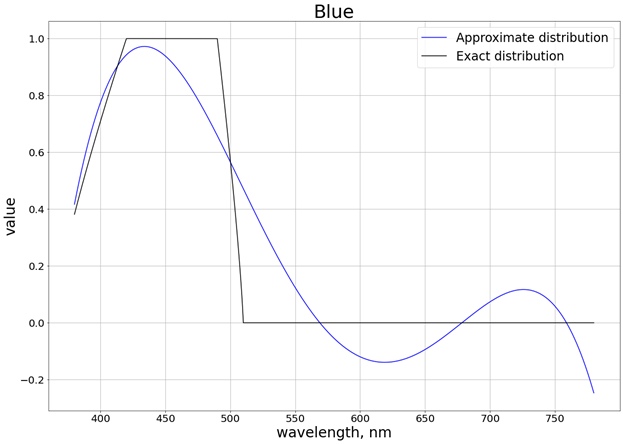
لضمان عدم تجاوز القيم لحد المقطع [0 ، 1] ، نستخدم الدالة saturate. بالنسبة للأحمر ، على سبيل المثال ، يتم الحصول على الوظيفة:

half GetRedWeight(half x)
{
    return saturate(0.8004883122689207 + 
    1.3673160565954385 * (-2.9000047500568042 + 0.005000012500149485 * x) - 
    1.244631137356407 * pow(-2.9000047500568042 + 0.005000012500149485 * x, 2) - 1.6053230172845554 * pow(-2.9000047500568042 + 0.005000012500149485*x, 3)+ 1.055933936470091 * pow(-2.9000047500568042 + 0.005000012500149485*x, 4));
}

المعلمات المفقودة startWaveLengthوفي endWaveLengthهذه الحالة هي 780 نانومتر و 380 نانومتر على التوالي. النتيجة في الممارسة sampleCount=3هي ما يلي (انظر حواف الصورة):

إذا قمنا بتعديل القيم ، فارتفع sampleCountإلى 400 ، ثم يصبح كل شيء أفضل:

للأسف ، لدينا عرض في الوقت الفعلي لا يمكننا فيه السماح بـ 400 عينة (حوالي 3-4) في جهاز تظليل واحد. لذلك ، قمنا بتقليل نطاق الطول الموجي قليلاً.

جزء من الطيف المرئي

لنأخذ مجموعة حتى ننتهي بكل من اللون الأحمر النقي والأزرق النقي. نرفض أيضًا الذيل الأحمر على اليسار ، لأنه يؤثر كثيرًا على كثير الحدود النهائي. ونتيجة لذلك نحصل على التوزيع على المقطع [440 ، 670]:

أيضًا ، ليست هناك حاجة إلى الاستيفاء على المقطع بالكامل ، حيث يمكننا الآن الحصول على كثير الحدود فقط للقطاع حيث تتغير القيمة. على سبيل المثال ، بالنسبة إلى اللون الأحمر ، هذا هو المقطع [510 ، 580] ، حيث تختلف قيمة الوزن من 0 إلى 1. في هذه الحالة ، يمكنك الحصول على كثير الحدود من الدرجة الثانية ، والذي يتم saturateتقليله أيضًا بواسطة الوظيفة إلى نطاق القيم [0 ، 1]. لجميع الألوان الثلاثة نحصل على النتيجة التالية مع مراعاة التشبع:

ونتيجة لذلك ، نحصل ، على سبيل المثال ، على كثير الحدود التالي للأحمر:

half GetRedWeight(half x)
{
    return saturate(0.5764348105166407 + 
    0.4761860550080825 * (-15.571636738012254 + 0.0285718367412005 * x) - 
    0.06265740390367036 * pow(-15.571636738012254 + 0.0285718367412005 * x, 2));
}

وعمليًا مع sampleCount=3:

في هذه الحالة ، مع الإعدادات الملتوية ، يتم الحصول على نفس النتيجة تقريبًا عند أخذ العينات عبر النطاق الكامل للطيف المرئي:

وهكذا ، مع كثيرات الحدود من الدرجة الثانية ، حصلنا على نتيجة جيدة في نطاق الطول الموجي من 440 نانومتر إلى 670 نانومتر.

الاقوي

بالإضافة إلى تحسين الحسابات من خلال كثيرات الحدود ، يمكنك تحسين عمل تظليل ، بالاعتماد على الآلية التي وضعناها على أساس الانحراف اللوني الجانبي لدينا ، أي عدم إجراء حسابات في المنطقة التي لا يتجاوز فيها الإزاحة الكلية البكسل الحالي ، وإلا فإننا سنأخذ نفس العينة بكسل ، ونحصل عليه.

تبدو هكذا:

bool isNotAberrated = abs(offsetDecrement.x * g_VS_ScreenSize.x) < 1.0 && abs(offsetDecrement.y * g_VS_ScreenSize.y) < 1.0;
if (isNotAberrated)
{
    OUT.Color.rgb = tex2Dlod(baseMap, half4(IN.baseTC, 0, 0)).rgb;
    return OUT;
}

التحسين صغير ولكنه فخور جدًا.

خاتمة

الزيغ اللوني الجانبي يبدو رائعًا جدًا ؛ هذا العيب لا يتداخل مع الرؤية في المركز. تعتبر فكرة تحليل الضوء في الأوزان تجربة مثيرة للغاية يمكن أن تعطي صورة مختلفة تمامًا إذا كان محركك أو لعبتك تسمح بأكثر من ثلاث عينات. في حالتنا ، كان من الممكن عدم الإزعاج والخروج بخوارزمية مختلفة ، لأنه حتى مع التحسينات لا يمكننا تحمل العديد من العينات ، وعلى سبيل المثال ، الفرق بين 3 و 5 عينات غير واضح للغاية. يمكنك تجربة الطريقة الموصوفة بنفسك ورؤية النتائج.

Armored Warfare: مشروع Armata. انحراف لوني