
يرتبط التحسين في الأعمال في الغالبية العظمى من الحالات باستخدام طريقة البرمجة الخطية. الطريقة مباشرة إلى حد ما. بالإضافة إلى ذلك ، هناك نظرية حول وجود وتفرد الحل.
ومع ذلك ، من الناحية العملية ، كل شيء ليس بسيطًا تمامًا.
المشكلة الأولى هي عدم خطية ظروف العالم الحقيقي. لكي تكون طريقة البرمجة الخطية قابلة للتطبيق ، يجب أن تكون خطية. هناك طرق لتعيين اللاخطية بشكل معقول من خلال المعادلات الخطية وعدم المساواة من خلال إدخال متغيرات جديدة ، وتحديد معاملات الوزن ، إلخ. عند حل مشاكل الإنتاج في هذه الحالة ، من الضروري العمل مع عدد كبير من المتغيرات ، وبالتالي المعادلات (عدم المساواة).
في نظرية حل المشاكل المتطرفة ، هناك نظرية حول استقرار الحلول لمشاكل البرمجة الخطية. وفقا لذلك ، فإن الحل يكون مستقرا فقط إذا كان مجال المشكلة محدبا. مع وجود عدد كبير من المتغيرات وعدم المساواة ، لا يمكن تحديد ما إذا كان نطاق المشكلة محدبًا. علاوة على ذلك ، فإن احتمال عدم التحدب مرتفع.
إذا لم تكن المشكلة مستقرة ، فعندئذٍ سيتم الحصول على نتائج مختلفة اعتمادًا على نقطة البداية لاجتياز القمم.
المشكلة الثانية- تقييد المتغير من الأسفل (x> h> 0). أي تطبيق لطريقة البرمجة الخطية سيوفر دائمًا قيمة غير صفرية. إذا كانت x تساوي بالضبط h ، فهذا يعني أن قيمة المتغير x يجب أن تكون صفرًا في الأساس. من الناحية العملية ، تتناثر هذه الأحجام "الخيالية" (طريقة التفرز) على متغيرات "ذات مغزى". نتيجة هذه الممارسة هي تآكل مفهوم الحل الأمثل ، وهو أمر مهم بشكل خاص إذا كان مثل هذا الحل واحدًا من العديد من الحلول في سلسلة القرار.
المشكلة الثالثة إدارية. تعطي طريقة البرمجة الخطية نتيجة واحدة فقط. وكيف ننظر إلى النتائج القريبة من المثلى؟ على سبيل المثال ، في الحل الناتج ، يكون تصنيف البائع ضعيفًا. كيفية فهم ما إذا كانت هناك حلول قريبة ، ولكن لموردين موثوق بهم.
مهمة النقل
يطابق المثال مشكلة البرمجة الخطية للنقل.
هناك 5 ناقلات (تم تحديد المهمة لنقل الفحم) ، والتي لها حسابان للتعريفة الجمركية. يمكن تغيير حدود التعريفات والتعريفات نفسها (يتم تعيينها بشكل بارزمي).

يتم تحديد النقل من نقطة إلى نقطة (وفقًا للطريقة المقبولة لنقل الفحم) والحجم.
نظرة عامة على الواجهة.

منطقة مهمة النقل.
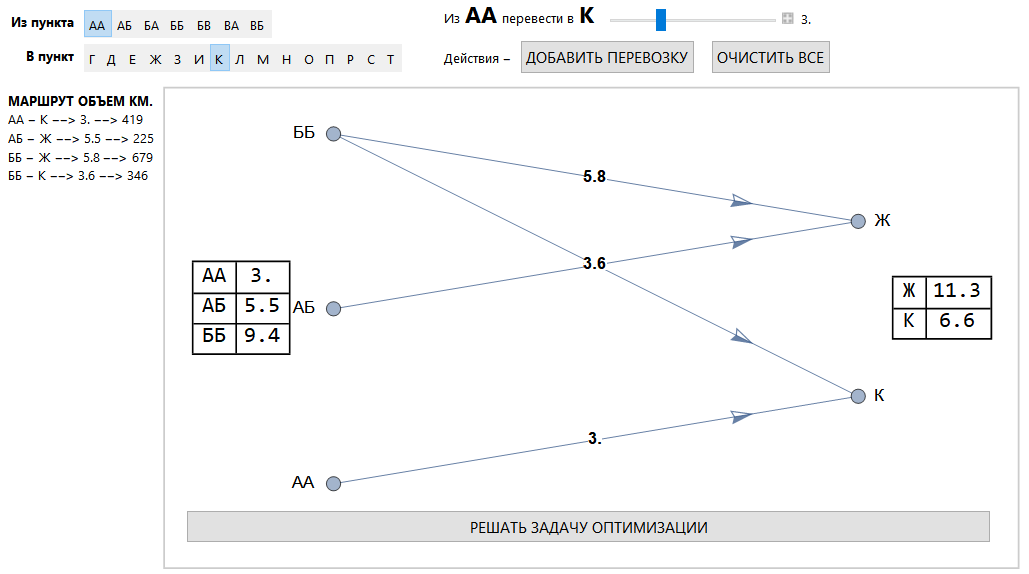
طريقة حل الكتلة
بدلاً من مشكلة برمجة خطية واحدة ، يتم حل مجموعة من المشاكل ، والتي يتوافق عددها مع جميع مجموعات التعريفات الممكنة. في الشحنة أعلاه ، يوجد 127 منها (القيمة الثانية في المستطيل الأيسر العلوي).

يتم اختيار الحلول المثلى من مجموعة المشاكل الصحيحة المتبقية. توفر كل مهمة حلاً مثالياً لمجموعة محددة من التعريفات. تشكل الحلول المعروضة أعلاه مجموعة معينة من الحدود القصوى.
لماذا طريقة الكتلة جيدة:
- هناك فهم لاستقرار الحل.
- لا توجد مجلدات "وهمية" للمتغيرات المحددة من الأسفل ، حيث سيكون هناك تركيبة أخرى حيث تكون هذه الحالة غائبة (حيث أن هذا المتغير غائب).
- يمكن إدخال الشروط الذاتية (التصنيفات ، التفضيلات) باستخدام طريقة البرمجة الخطية القياسية.
مع وجود عدد أكبر من الشحنات ، لدينا الصورة التالية (جزء).
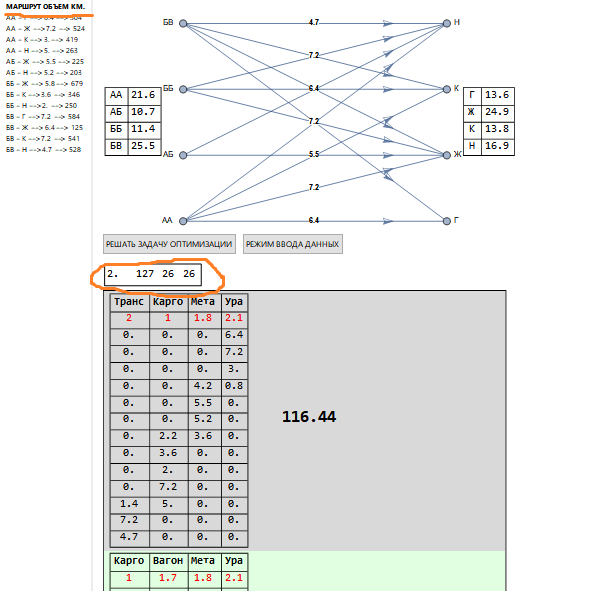
في الزاوية اليسرى العليا في المستطيل فوق الحلول (مظللة باللون البرتقالي) ، يشار إلى قيم أخرى أكثر من قبل: 127 - تركيبات (كما كان من قبل ، والتي تتعلق ببنية جداول التعريفات) ، 26 - تتوافق مع عدد المشاكل الصحيحة التي يتم حلها. يشار إلى التعريفة المستخدمة باللون الأحمر تحت اسم الناقل ، وأعمدة النقل تتوافق مع قائمة المسارات (مسطرة باللون البرتقالي).
من المهم ملاحظة أن الطريقة المستخدمة تسمح لك بفهم النتيجة وتقييم الحلول المماثلة واستخدام تجربتك المهنية عند اختيار البدائل ، مع الأخذ في الاعتبار تعقيدات إدارة عمل معين.