التعلم الآلي (ML) يغير العالم بالفعل. تستخدم Google IO لتقديم وعرض الردود على عمليات بحث المستخدم. تستخدمه Netflix للتوصية بالأفلام في المساء. ويستخدمه Facebook لاقتراح أصدقاء جدد قد تعرفهم.
لم يكن التعلم الآلي أكثر أهمية من أي وقت مضى ، وفي الوقت نفسه ، كان من الصعب جدًا تعلمه. هذه المنطقة مليئة بالمصطلحات اللغوية ، ويتزايد عدد خوارزميات ML المختلفة كل عام.
ستعرفك هذه المقالة على المفاهيم الأساسية في التعلم الآلي. وبشكل أكثر تحديدًا ، سنناقش المفاهيم الأساسية لأهم 9 خوارزميات ML اليوم.
نظام التوصية
يتطلب بناء نظام توصية كامل من 0 معرفة عميقة بالجبر الخطي. ولهذا السبب ، إذا لم تكن قد درست هذا النظام من قبل ، فقد يكون من الصعب عليك فهم بعض المفاهيم الواردة في هذا القسم.
ولكن لا تقلق - مكتبة Python-scikit للتعلم تجعل من السهل جدًا إنشاء CP. لذلك لا تحتاج إلى تلك المعرفة العميقة بالجبر الخطي لبناء CP عامل.
كيف يعمل CP؟
هناك نوعان رئيسيان من أنظمة التوصيات:
- قائم على المحتوى
- تصفية التعاونية
يقدم النظام المستند إلى المحتوى توصيات بناءً على تشابه العناصر التي استخدمتها بالفعل. تتصرف هذه الأنظمة تمامًا بالطريقة التي تتوقع أن يتصرف بها الإنتاج الأنظف.
توفر تصفية CP التعاونية توصيات تستند إلى المعرفة بكيفية تفاعل المستخدم مع العناصر (* ملاحظة: يتم أخذ التفاعلات مع عناصر المستخدمين الآخرين التي تتشابه في السلوك مع المستخدم كأساس). وبعبارة أخرى ، يستخدمون "حكمة الجمهور" (ومن ثم "التعاونية" باسم الطريقة).
في العالم الحقيقي ، تعد تصفية CP التعاونية أكثر شيوعًا من النظام القائم على المحتوى. هذا يرجع بشكل رئيسي إلى حقيقة أنها عادة ما تعطي نتائج أفضل. يجد بعض الخبراء أيضًا أن النظام التعاوني أسهل في الفهم.
يحتوي التصفية التعاونية CP أيضًا على ميزة فريدة لا توجد في نظام قائم على المحتوى. أي أن لديهم القدرة على تعلم الميزات بأنفسهم.
وهذا يعني أنها قد تبدأ في تعريف التشابه في العناصر بناءً على الخصائص أو السمات التي لم توفرها حتى يعمل هذا النظام.
هناك فئتان فرعيتان للتصفية التعاونية:
- على أساس النموذج
- على أساس الجوار
الخبر السار هو أنك لست بحاجة إلى معرفة الفرق بين هذين النوعين من التصفية التعاونية CP للنجاح في ML. يكفي فقط أن تعرف أن هناك عدة أنواع.
لخص
في ما يلي ملخص سريع لما تعلمناه عن نظام التوصيات في هذه المقالة:
- أمثلة على نظام التوصيات الواقعي
- أنواع مختلفة من نظام التوصيات ولماذا يتم استخدام التصفية التعاونية في كثير من الأحيان أكثر من النظام القائم على المحتوى
- العلاقة بين نظام التوصية والجبر الخطي
الانحدارالخطي
يستخدم الانحدار الخطي للتنبؤ بقيمة y بناءً على مجموعة من قيم x.
تاريخ الانحدار الخطي
اخترع فرانسيس جالتون الانحدار الخطي (LR) في عام 1800. كان غالتون عالماً يدرس العلاقة بين الآباء والأطفال. وبشكل أكثر تحديدًا ، درس غالتون العلاقة بين نمو الآباء ونمو أبنائهم. كان اكتشاف غالتون الأول هو حقيقة أن نمو الأبناء ، كقاعدة عامة ، كان تقريبًا مثل نمو آبائهم. وهو ليس مفاجئا.
في وقت لاحق ، اكتشف غالتون شيئًا أكثر إثارة للاهتمام. كان نمو الابن ، كقاعدة عامة ، أقرب إلى متوسط الارتفاع الكلي لجميع الناس منه إلى نمو والده.
دعا غالتون هذه الظاهرة الانحدار . على وجه التحديد ، قال: "يميل ارتفاع الابن إلى التراجع (أو التحول نحو) متوسط الارتفاع".
أدى هذا إلى مجال كامل في الإحصاء وتعلم الآلة يسمى الانحدار.
رياضيات الانحدار الخطي
في عملية إنشاء نموذج الانحدار ، كل ما نحاول القيام به هو رسم خط قريب من كل نقطة في مجموعة البيانات قدر الإمكان.
مثال نموذجي على هذا النهج هو الانحدار الخطي "المربعات الصغرى" ، التي تحسب قرب خط في الاتجاه من أعلى إلى أسفل.
مثال للتوضيح:
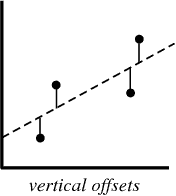
عند إنشاء نموذج انحدار ، فإن منتجك النهائي عبارة عن معادلة يمكنك استخدامها للتنبؤ بقيم y للقيمة x دون معرفة القيمة y مقدمًا.
الانحدار اللوجستي
يتشابه الانحدار اللوجستي مع الانحدار الخطي ، باستثناء حقيقة أنه بدلاً من حساب قيمة y ، فإنه يقيم الفئة التي تنتمي إليها نقطة بيانات معينة.
ما هو الانحدار اللوجستي؟
الانحدار اللوجستي هو نموذج للتعلم الآلي يستخدم لحل مشاكل التصنيف.
فيما يلي بعض الأمثلة على مهام تصنيف MO:
- البريد الإلكتروني العشوائي (البريد العشوائي أم لا
- مطالبة التأمين على السيارات (تعويض أم إصلاح؟)
- تشخيص الأمراض
من الواضح أن لكل مهمة من هذه المهام فئتان ، مما يجعلها أمثلة على مهام التصنيف الثنائية.
يعمل الانحدار اللوجستي بشكل جيد مع مشاكل التصنيف الثنائي - نحن ببساطة نقوم بتعيين فئات مختلفة إلى 0 و 1 ، على التوالي.
لماذا الانحدار اللوجستي؟ لأنه لا يمكنك استخدام الانحدار الخطي لتوقعات التصنيف الثنائي. لن يعمل ببساطة لأنك ستحاول رسم خط مستقيم من خلال مجموعة بيانات ذات قيمتين محتملتين.
يمكن أن تساعدك هذه الصورة في فهم سبب أن الانحدار الخطي سيئ بالنسبة للتصنيف الثنائي:
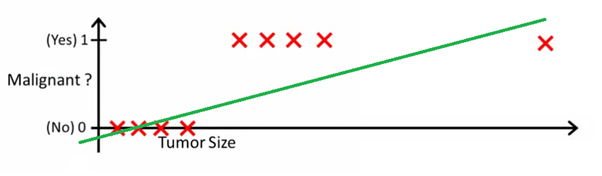
في هذه الصورة ، يمثل المحور ص احتمالية أن يكون الورم خبيثًا. تمثل قيم 1-y احتمالية أن يكون الورم حميداً. كما ترى ، فإن أداء نموذج الانحدار الخطي ضعيف جدًا للتنبؤ باحتمالية معظم الملاحظات في مجموعة البيانات.
هذا هو السبب في أن نموذج الانحدار اللوجستي مفيد. لديها انحناء نحو أفضل خط مناسب ، مما يجعلها أكثر ملاءمة للتنبؤ بالبيانات النوعية (الفئوية).
فيما يلي مثال يقارن بين نماذج الانحدار الخطي واللوجستي على نفس البيانات:
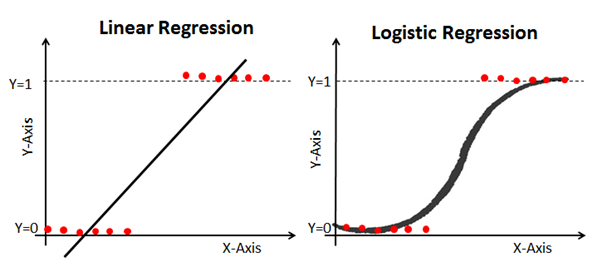
السيني (وظيفة السيني)
سبب الانحدار اللوجستي هو أنه لا يستخدم معادلة خطية لحسابها. بدلاً من ذلك ، تم بناء نموذج الانحدار اللوجستي باستخدام السيني (يسمى أيضًا دالة لوجستية لأنه يُستخدم في الانحدار اللوجستي).
لست مضطرًا إلى حفظ السيني تمامًا للنجاح في ML. ومع ذلك ، سيكون من المفيد الحصول على فكرة عن هذه الميزة.
الصيغة السينية:
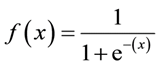
السمة الرئيسية للسيني السيني ، والتي تستحق التعامل معها - بغض النظر عن القيمة التي تمررها إلى هذه الوظيفة ، فإنها ستعيد دائمًا القيمة في النطاق 0-1.
استخدام نموذج الانحدار اللوجستي للتنبؤات
من أجل استخدام الانحدار اللوجستي للتنبؤات ، تحتاج عادةً إلى تحديد نقطة القطع بدقة. عادة ما تكون نقطة القطع 0.5.
دعونا نستخدم مثال تشخيص السرطان من الرسم البياني السابق لرؤية هذا المبدأ في الممارسة. إذا أعاد نموذج الانحدار اللوجستي قيمة أقل من 0.5 ، فسيتم تصنيف نقطة البيانات هذه على أنها حميدة. وبالمثل ، إذا أعطى السيني قيمة أعلى من 0.5 ، فسيتم تصنيف الورم على أنه خبيث.
استخدام مصفوفة خطأ لقياس فعالية الانحدار اللوجستي
يمكن استخدام مصفوفة الخطأ كأداة لمقارنة العلامات الإيجابية والسلبية الحقيقية والسلبية الكاذبة والسلبية الكاذبة في MO.
مصفوفة الخطأ مفيدة بشكل خاص عند استخدامها لقياس أداء نموذج الانحدار اللوجستي. في ما يلي مثال لكيفية استخدام مصفوفة الخطأ:
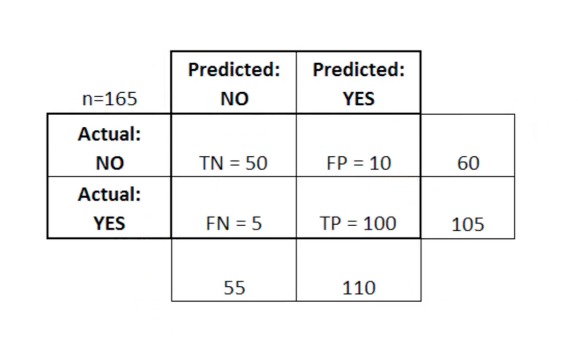
في هذا الجدول ، يشير TN إلى سلبي حقيقي ، و FN يشير إلى سلبي كاذب ، و FP يشير إلى إيجابي كاذب ، TP يشير إلى إيجابي حقيقي.
مصفوفة الخطأ مفيدة لتقييم نموذج إذا كان هناك أرباع "ضعيفة" في مصفوفة الخطأ. كمثال ، قد يكون لديها عدد غير طبيعي من الإيجابيات الكاذبة.
من المفيد أيضًا في بعض الحالات التأكد من أن نموذجك يعمل بشكل صحيح في منطقة خطرة بشكل خاص من مصفوفة الخطأ.
في هذا المثال لتشخيص السرطان ، على سبيل المثال ، ترغب في التأكد من أن نموذجك لا يحتوي على الكثير من الإيجابيات الخاطئة لأن هذا يعني أنك قمت بتشخيص الورم الخبيث لشخص ما على أنه حميد.
لخص
في هذا القسم ، كان لديك أول معارفك لنموذج ML - الانحدار اللوجستي.
في ما يلي ملخص سريع لما تعلمته عن الانحدار اللوجستي:
- أنواع مشاكل التصنيف المناسبة لحل الانحدار اللوجستي
- تعطي الوظيفة اللوجستية (السينية) دائمًا قيمة بين 0 و 1
- كيفية استخدام نقاط التوقف للتنبؤ بنموذج الانحدار اللوجستي
- لماذا تعتبر مصفوفة الخطأ مفيدة لقياس أداء نموذج الانحدار اللوجستي
خوارزمية K- أقرب الجيران
يمكن أن تساعد خوارزمية k- الجوار الأقرب في حل مشكلة التصنيف في الحالة عندما يكون هناك أكثر من فئتين.
ما هي خوارزمية الجيران الأقرب؟
هذه خوارزمية تصنيف مبنية على مبدأ بسيط. في الواقع ، المبدأ بسيط للغاية بحيث أنه من الأفضل إظهاره بمثال.
تخيل أن لديك بيانات الطول والوزن للاعبي كرة القدم ولاعبي كرة السلة. يمكن استخدام خوارزمية أقرب الجيران للتنبؤ بما إذا كان اللاعب الجديد لاعب كرة قدم أم لاعب كرة سلة. للقيام بذلك ، تحدد الخوارزمية نقاط بيانات K الأقرب إلى كائن الدراسة.
توضح هذه الصورة هذا المبدأ مع المعلمة K = 3:
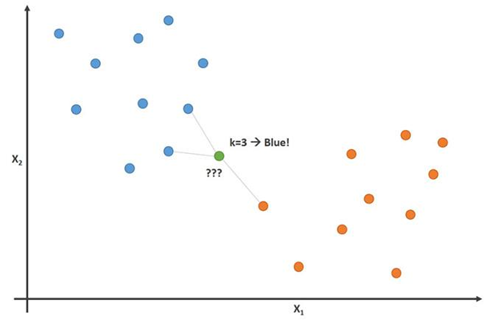
في هذه الصورة ، لاعبو كرة القدم أزرقون ولاعبو كرة السلة برتقاليون. النقطة التي نحاول تصنيفها هي باللون الأخضر. نظرًا لأن معظم (2 من 3) العلامات الأقرب إلى النقطة الخضراء هي اللون الأزرق (لاعبي كرة القدم) ، فإن خوارزمية K المجاورة الأقرب تتوقع أن اللاعب الجديد سيكون أيضًا لاعب كرة قدم.
كيفية بناء خوارزمية K المجاورة الأقرب
الخطوات الرئيسية لبناء هذه الخوارزمية:
- اجمع كل البيانات
- احسب المسافة الإقليدية من نقطة البيانات الجديدة x إلى جميع النقاط الأخرى في مجموعة البيانات
- فرز النقاط من مجموعة البيانات بترتيب تصاعدي للمسافة إلى x
- توقع الإجابة باستخدام نفس الفئة مثل معظم البيانات الأقرب لـ K إلى x
أهمية المتغير K في خوارزمية الجوار K- الأقرب
على الرغم من أن هذا قد لا يكون واضحًا منذ البداية ، إلا أن تغيير قيمة K في هذه الخوارزمية سيغير الفئة التي تقع فيها نقطة البيانات الجديدة.
وبشكل أكثر تحديدًا ، ستتسبب قيمة K المنخفضة جدًا في أن يتنبأ نموذجك بدقة في مجموعة بيانات التدريب ، ولكن تكون غير فعالة للغاية في بيانات الاختبار. أيضًا ، وجود ارتفاع عالٍ في K سيجعل النموذج معقدًا بلا داع.
يوضح الرسم التوضيحي أدناه هذا التأثير بشكل مثالي:
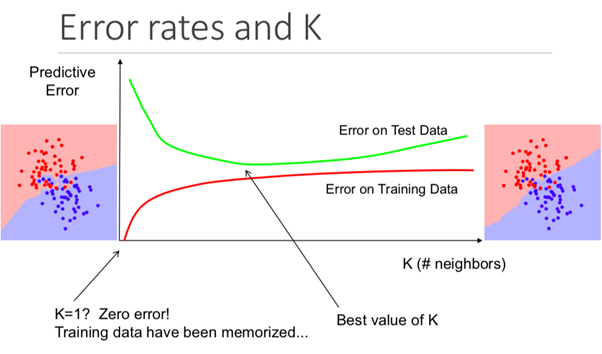
إيجابيات وسلبيات خوارزمية K المجاورة الأقرب
لتلخيص الألفة مع هذه الخوارزمية ، دعنا نناقش بإيجاز إيجابيات وسلبيات استخدامها.
الإيجابيات:
- الخوارزمية بسيطة وسهلة الفهم
- تدريب نموذج تافه على بيانات التدريب الجديدة
- يعمل مع أي عدد من الفئات في مهمة تصنيف
- أضف المزيد من البيانات بسهولة إلى الكثير من البيانات
- يأخذ النموذج معلمتين فقط: K ومقياس المسافة الذي ترغب في استخدامه (عادة المسافة الإقليدية)
السلبيات:
- تكلفة حساب عالية ، لأن تحتاج إلى معالجة كمية البيانات بالكامل
- لا يعمل بشكل جيد مع المعلمات الفئوية
لخص
ملخص لما تعلمته للتو عن خوارزمية K-Nearest Neighbor:
- مثال على مشكلة التصنيف (لاعبي كرة القدم أو كرة السلة) التي يمكن أن تحلها الخوارزمية
- كيف تستخدم الخوارزمية المسافة الإقليدية إلى النقاط المجاورة للتنبؤ بالفئة التي تنتمي إليها نقطة البيانات الجديدة
- لماذا تعتبر قيم K مهمة للتنبؤ
- إيجابيات وسلبيات استخدام خوارزمية K المجاورة الأقرب
أشجار القرار والغابات العشوائية
شجرة القرار والغابة العشوائية مثالان لطريقة الشجرة. بتعبير أدق ، أشجار القرار هي نماذج ML تستخدم للتنبؤ من خلال التكرار عبر كل وظيفة في مجموعة بيانات واحدة تلو الأخرى. الغابة العشوائية هي مجموعة (لجنة) من أشجار القرار التي تستخدم أوامر عشوائية من الكائنات في مجموعة بيانات.
ما هي طريقة الشجرة؟
قبل أن نغوص في الأسس النظرية للطريقة القائمة على الشجرة في ML ، من المفيد أن نبدأ بمثال.
تخيل أنك تلعب كرة السلة كل يوم إثنين. علاوة على ذلك ، فأنت دائمًا تدعو نفس الصديق للمجيء واللعب معك. في بعض الأحيان يأتي صديق ، في بعض الأحيان لا يأتي. يعتمد قرار القدوم أو لا على عدة عوامل: أي نوع من الطقس ودرجة الحرارة والرياح والتعب. تبدأ في ملاحظة هذه الميزات وتتبعها مع قرار صديقك اللعب أم لا.
يمكنك استخدام هذه البيانات للتنبؤ بما إذا كان صديقك قادم اليوم أم لا. إحدى التقنيات التي يمكنك استخدامها هي شجرة القرار. هكذا تبدو:
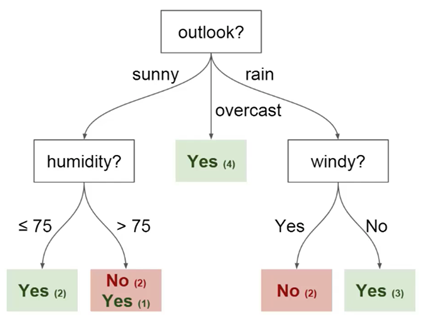
تحتوي كل شجرة قرارات على نوعين من العناصر:
- العقد: الأماكن التي يتم فيها تقسيم الشجرة بناءً على قيمة معلمة معينة
- الحواف: نتيجة الانقسام المؤدي إلى العقدة التالية
يمكنك أن ترى أن الرسم البياني يحتوي على عقد للتوقعات والرطوبة
والعاصفة. وكذلك الجوانب لكل قيمة محتملة لكل من هذه المعلمات.
إليك بعض التعريفات الأخرى التي يجب أن تفهمها قبل أن نبدأ:
- الجذر - العقدة التي يبدأ منها تقسيم الشجرة
- الأوراق - العقد النهائية التي تتنبأ بالنتيجة النهائية
لديك الآن فهم أساسي لما هي شجرة القرار. سنلقي نظرة على كيفية بناء مثل هذه الشجرة من البداية في القسم التالي.
كيفية بناء شجرة القرار من الصفر
بناء شجرة القرار أصعب مما يبدو. وذلك لأن تحديد العواقب (الخصائص) لتقسيم بياناتك إلى (وهو موضوع من الإنتروبيا والحصول على البيانات) هو مهمة صعبة من الناحية الرياضية.
لحل هذه المشكلة ، يستخدم متخصصو ML عادة العديد من أشجار القرار ، ويطبقون مجموعات عشوائية من الخصائص المختارة لتقسيم الشجرة إليهم. وبعبارة أخرى ، يتم اختيار مجموعات عشوائية جديدة من الخصائص لكل شجرة منفصلة ، في كل قسم منفصل. تسمى هذه التقنية الغابات العشوائية.
بشكل عام ، يختار الخبراء عادةً حجم مجموعة عشوائية من الميزات (يُشار إليها بـ m) بحيث يكون الجذر التربيعي لإجمالي عدد الميزات في مجموعة البيانات (يُشار إليه بـ p). باختصار ، m هو الجذر التربيعي لـ p ، ثم يتم اختيار خاصية معينة بشكل عشوائي من m.
فوائد استخدام غابة عشوائية
تخيل أنك تعمل مع الكثير من البيانات التي لها خاصية "قوية" واحدة. وبعبارة أخرى ، هناك خاصية في مجموعة البيانات هذه يمكن توقعها من حيث النتيجة النهائية أكثر من الخصائص الأخرى لمجموعة البيانات هذه.
إذا كنت تقوم ببناء شجرة قرارات يدويًا ، فمن المنطقي استخدام هذه الخاصية للقسم "العلوي" في شجرتك. هذا يعني أنه سيكون لديك العديد من الأشجار التي ترتبط تنبؤاتها ارتباطًا وثيقًا.
نريد تجنب هذا بسبب باستخدام متوسط المتغيرات عالية الارتباط لا يقلل التباين بشكل كبير. باستخدام مجموعات عشوائية من الخصائص لكل شجرة في غابة عشوائية ، نقوم بتزيين الأشجار وتقليل تباين النموذج الناتج. تعتبر علاقة الديكور هذه ميزة رئيسية في استخدام الغابات العشوائية على أشجار القرار المصنوعة يدويًا.
لخص
إذن هذا ملخص سريع لما تعلمته للتو عن أشجار القرار والغابات العشوائية:
- مثال على مشكلة يمكن توقع حلها باستخدام شجرة قرارات
- عناصر شجرة القرار: العقد والوجوه والجذور والأوراق
- كيف يسمح لنا استخدام مجموعة عشوائية من الخصائص ببناء غابة عشوائية
- لماذا يمكن أن يكون استخدام غابة عشوائية لربط المتغيرات مفيدًا في تقليل تباين النموذج الناتج
دعم آلات المتجهات
آلات ناقلات الدعم هي خوارزمية تصنيف (على الرغم من أنها ، من الناحية الفنية ، يمكن استخدامها أيضًا لحل مشاكل الانحدار) التي تقسم مجموعة من البيانات إلى فئات في أكبر "الفجوات" بين الفئات. يصبح هذا المفهوم أكثر وضوحًا عند إلقاء نظرة على المثال التالي.
ما هو دعم آلة النواقل؟
جهاز ناقل الدعم (SVM) هو نموذج ML خاضع للإشراف مع خوارزميات تعلم مناسبة تحلل البيانات وتتعرف على الأنماط. يمكن استخدام SVM لكل من مهام التصنيف وتحليل الانحدار. في هذه المقالة ، سوف ننظر على وجه التحديد في استخدام آلات ناقلات الدعم لحل مشاكل التصنيف.
كيف تعمل مذكرة التفاهم؟
دعونا نتعمق أكثر في كيفية عمل مذكرة التفاهم حقًا.
يتم إعطاؤنا مجموعة من الأمثلة التدريبية ، يتم تمييز كل منها على أنه ينتمي إلى واحدة من فئتين ، وباستخدام هذه المجموعة من SVMs نقوم ببناء نموذج. يصنف هذا النموذج أمثلة جديدة في واحدة من فئتين. وهذا يجعل SVM مصنفًا ثنائيًا غير محتمل.
تستخدم مذكرة التفاهم الهندسة لإجراء التنبؤات حسب الفئة. بشكل أكثر تحديدًا ، تقوم آلة المتجه الداعمة بتعيين نقاط البيانات كنقاط في الفضاء وتصنيفها بحيث يتم فصلها بأكبر فجوة ممكنة. يعتمد التوقع بأن نقاط البيانات الجديدة ستنتمي إلى فئة معينة على أي جانب من نقطة الاستراحة.
في ما يلي مثال مرئي لمساعدتك على فهم حدس مذكرة التفاهم:
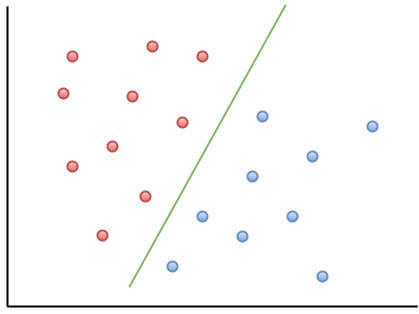
كما يمكنك أن تلاحظ ، إذا وقعت نقطة بيانات جديدة على يسار الخط الأخضر ، فسيتم الإشارة إليها على أنها "حمراء" ، وإذا كانت على اليمين ، فسيتم الإشارة إليها باسم "أزرق". يُطلق على هذا الخط الأخضر اسم "hyperplane" وهو مصطلح مهم للعمل مع مذكرات التفاهم.
دعنا نلقي نظرة على التمثيل المرئي التالي لـ SVM:
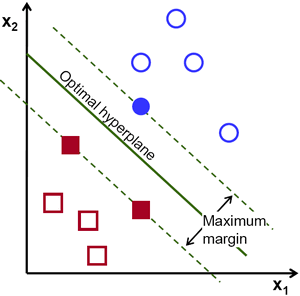
في هذا الرسم البياني ، يتم وصف الطائرة الزائدة بأنها "الطائرة الزائدة المثلى". تحدد نظرية الدعم لآلة المتجهات السطح الزائد المثالي على أنه السطح الزائد الذي يزيد من المجال بين أقرب نقطتي بيانات من فئات مختلفة.
كما ترى ، تؤثر حدود المجال بالفعل على 3 نقاط بيانات - 2 من الفئة الحمراء و 1 من اللون الأزرق. تسمى هذه النقاط ، التي تتلامس مع حدود المجال ، نواقل الدعم - ومن هنا جاء الاسم.
لخص
في ما يلي لقطة سريعة لما تعلمته للتو عن دعم أجهزة المتجه:
- مذكرة التفاهم هي مثال لخوارزمية ML خاضعة للإشراف
- يمكن استخدام ناقل الدعم لحل مشاكل التصنيف وتحليل الانحدار.
- كيف تقوم مذكرة التفاهم بتصنيف البيانات باستخدام طائرة مفرطة تضخم الهامش بين الفئات في مجموعة البيانات
- تسمى نقاط البيانات التي تلمس حدود مجال التقسيم ناقلات الدعم. هذا هو المكان الذي يأتي منه اسم الطريقة.
K- يعني التكتل
طريقة K-Means هي خوارزمية تعلم آلي بدون إشراف. هذا يعني أنه يقبل البيانات غير المميزة ويحاول تجميع مجموعات من الملاحظات المماثلة في بياناتك. تعتبر طريقة K-Means مفيدة للغاية في حل التطبيقات الواقعية. فيما يلي أمثلة على العديد من المهام التي تناسب هذا النموذج:
- تجزئة العملاء لفرق التسويق
- تصنيف الوثائق
- تحسين طرق الشحن لشركات مثل Amazon أو UPS أو FedEx
- التعرف على المواقع الإجرامية في المدينة والرد عليها
- تحليلات رياضية محترفة
- التنبؤ بالجرائم الإلكترونية ومنعها
الهدف الرئيسي من طريقة K-Means هو تقسيم مجموعة البيانات إلى مجموعات مميزة بحيث تكون العناصر داخل كل مجموعة متشابهة مع بعضها البعض.
فيما يلي تمثيل مرئي لما يبدو عليه في الممارسة:
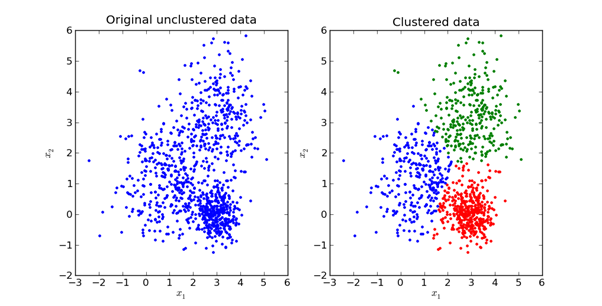
سنستكشف الرياضيات الكامنة وراء طريقة K-Means في القسم التالي من هذه المقالة.
كيف تعمل طريقة K-Means؟
الخطوة الأولى في استخدام طريقة K-Means هي اختيار عدد المجموعات التي تريد تقسيم بياناتك إليها. هذه الكمية هي قيمة K ، تنعكس في اسم الخوارزمية. إن اختيار قيمة K في طريقة K-Means أمر مهم للغاية. سنناقش كيفية اختيار قيمة K الصحيحة بعد ذلك بقليل. بعد
ذلك ، يجب عليك تحديد نقطة بشكل عشوائي في مجموعة البيانات وتعيينها لمجموعة عشوائية. سيمنحك هذا موضع بيانات البدء الذي تقوم فيه بتشغيل التكرار التالي حتى تتوقف المجموعات عن التغيير:
- حساب السنتويد (مركز الثقل) لكل عنقود بأخذ متجه النقاط في تلك المجموعة
- إعادة تعيين كل نقطة بيانات إلى الكتلة التي يكون مركزها المركزي هو الأقرب إلى النقطة
اختيار قيمة K مناسبة في طريقة K-Means
بالمعنى الدقيق للكلمة ، فإن اختيار قيمة K المناسبة أمر صعب للغاية. لا توجد إجابة "صحيحة" في اختيار القيمة "الأفضل" لـ K. إحدى الطرق التي يستخدمها متخصصو ML في كثير من الأحيان تسمى "طريقة الكوع".
لاستخدام هذه الطريقة ، فإن أول شيء عليك القيام به هو حساب مجموع الأخطاء المربعة - الانحراف المعياري لخوارزميتك لمجموعة من قيم K. يتم تعريف الانحراف المعياري في طريقة K-يعني مجموع مربعات المسافات بين كل نقطة بيانات في المجموعة. ومركز ثقل هذه الكتلة.
كمثال على هذه الخطوة ، يمكنك حساب الانحراف المعياري لقيم K من 2 و 4 و 6 و 8 و 10. بعد ذلك ، ستحتاج إلى إنشاء رسم بياني للانحراف المعياري وقيم K هذه. سترى أن الانحراف ينخفض كلما زادت قيمة K.
ومن المنطقي: أنه كلما زاد عدد الفئات التي تقوم بإنشائها من مجموعة بيانات ، زادت احتمالية أن تكون كل نقطة بيانات قريبة من مركز مجموعة تلك النقطة.
مع ذلك ، فإن الفكرة الرئيسية وراء طريقة الكوع هي اختيار القيمة K التي ستبطئ RMS عندها بشكل كبير من معدل الانخفاض. يشكل هذا الانخفاض الحاد "كوعًا" على الرسم البياني.
كمثال ، هنا مخطط RMS مقابل K. في هذه الحالة ، ستقترح طريقة الكوع استخدام قيمة K تبلغ حوالي 6. من
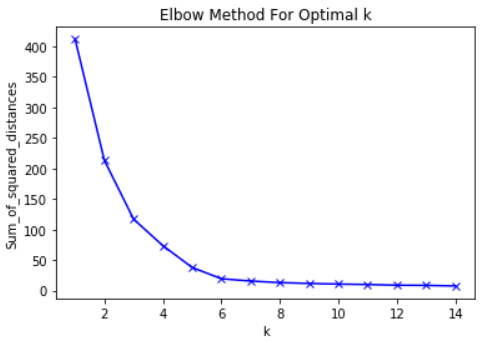
المهم أن K = 6 هو مجرد تقدير لقيمة K مقبولة. لا توجد قيمة K "أفضل" في طريقة K-Means. مثل العديد من الأشياء في ML ، هذا قرار ظرفية للغاية.
لخص
إليك رسم سريع لما تعلمته للتو في هذا القسم:
- أمثلة لمهام ML بدون معلم يمكن حلها بطريقة K-يعني
- المبادئ الأساسية لطريقة K- الوسائل
- كيف يعمل K-Means
- كيفية استخدام طريقة الكوع لتحديد القيمة المناسبة للمعلمة K في هذه الخوارزمية
تحليل المكونات الرئيسية
يتم استخدام تحليل المكون الرئيسي لتحويل مجموعة البيانات مع العديد من المعلمات إلى مجموعة بيانات جديدة مع معلمات أقل ، وكل معلمة جديدة في مجموعة البيانات هذه هي مزيج خطي من المعلمات الموجودة مسبقًا. تميل هذه البيانات المحولة إلى تبرير الكثير من التباين في مجموعة البيانات الأصلية مع المزيد من البساطة.
ما هي طريقة المكون الرئيسي؟
تحليل المكون الرئيسي (PCA) هو تقنية ML تُستخدم لدراسة العلاقات بين مجموعات المتغيرات. وبعبارة أخرى ، تدرس PCA مجموعات من المتغيرات لتحديد البنية الأساسية لهذه المتغيرات. ويطلق على الأنيسول الخماسي الكلور أحيانًا تحليل العوامل.
بناءً على هذا الوصف ، قد تعتقد أن الأنيسول الخماسي الكلور يشبه إلى حد كبير الانحدار الخطي. ولكن هذا ليس هو الحال. في الواقع ، هناك اختلافات مهمة بين هاتين التقنيتين.
الاختلافات بين الانحدار الخطي والأنيسول الخماسي الكلور
يحدد الانحدار الخطي الخط الأكثر ملاءمة عبر مجموعة البيانات. يحدد تحليل المكون الرئيسي العديد من الخطوط المتعامدة الأكثر ملاءمة لمجموعة بيانات.
إذا لم تكن على دراية بمصطلح التعامدي ، فهذا يعني ببساطة أن الخطوط بزاوية قائمة لبعضها البعض ، مثل الشمال والشرق والجنوب والغرب على الخريطة.
دعونا نلقي نظرة على مثال لمساعدتك على فهم هذا بشكل أفضل.

ألق نظرة على ملصقات المحور في هذه الصورة. يشرح المكون الرئيسي للمحور السيني 73٪ من التباين في مجموعة البيانات هذه. يشرح المكون الرئيسي للمحور ص حوالي 23٪ من التباين في مجموعة البيانات.
وهذا يعني أن 4٪ من التباين يبقى غير مبرر. يمكنك تقليل هذا الرقم عن طريق إضافة المزيد من المكونات الرئيسية إلى التحليل الخاص بك.
لخص
ملخص لما تعلمته للتو عن تحليل المكون الرئيسي:
- يحاول PCA العثور على العوامل المتعامدة التي تحدد التباين في مجموعة البيانات
- الفرق بين الانحدار الخطي والأنيسول الخماسي الكلور
- كيف تبدو المكونات الرئيسية المتعامدة عند تقديمها في مجموعة بيانات
- يمكن أن تساعد إضافة مكونات رئيسية إضافية في تفسير التباين بشكل أكثر دقة في مجموعة البيانات