
مقالات دورة أخرى
في هذا الجزء الرابع ، نكمل وصف تشفير AES - 128. بالنسبة للقراء الذين ليسوا على دراية بالأجزاء السابقة من العمل ، سأوضح أن المادة مقدمة للأغراض التعليمية وهذا يفرض عددًا من الميزات (التفاصيل والأمثلة العددية والأسس الرياضية ، وما إلى ذلك) ليس المقصود فقط التعرف على المعيار ، واستخدام المواد المقدمة لتطوير خوارزميات التشفير وفك التشفير (في حالة عدم وجود مفتاح). لم يضع مؤلفو العديد من المنشورات المعروفة على الإنترنت (وغير المتصلة بالإنترنت) أنفسهم مثل هذه الأهداف ، مما يجعل هذه المنشورات قليلة الاستخدام لأغراضنا.
تسمى العملية العكسية للتشفير فك تشفير الرسائل. لفك تشفير (مع مفتاح) التشفير (PCT) ، يتم إنشاء جدول استبدال عكسي ومفاتيح مستديرة ، والتي يتم استخدامها بترتيب عكسي بالنسبة لمخطط التشفير ، ولكنها تشبه عملية التشفير.
فك تشفير رسائل AES
تظل قائمة عمليات فك تشفير إحدى الرسائل كما هي بالنسبة للتشفير. يمكن العثور على مزيد من التفاصيل حول العمليات هنا . هذا هو مبدأ عام إلى حد ما من الشفرات - تنفيذ جهاز واحد للتشفير وفك التشفير ، والذي يتم توفيره من خلال مجموعات من نفس الوظائف لكلتا العمليتين. يتم تغيير النص المصدر وتسلسل تسليم المفتاح فقط.
يتم تنفيذ عملية فك تشفير الرسائل كتسلسل للتحويلات العكسية (العكسية) المستخدمة للتشفير ، بالترتيب العكسي لتسلسلها أثناء التشفير. من الواضح أيضًا أن المفاتيح الدائرية تُستخدم بالتسلسل المناسب: أولاً ، المفتاح الذي تم استلامه أخيرًا ، ثم المفتاح قبل الأخير ، وهكذا حتى المفتاح الدائري الأول.
تظل جميع أسماء التحويل كما هي ، ولكن مسبوقة بـ Inv. سننظر فيها في نفس التسلسل كما كان من قبل. يسمح تشفير AES بخيارين لفك التشفير ، للخلف وللأمام ، والتي تتم مناقشتها بالتفصيل أدناه.
خيار فك التشفير العكسي
يعد فك التشفير العكسي للرسالة عملية طبيعية لعكس عملية التشفير.
تظل عملية AddRoundKey كما هي (بدون تغيير) S + Ki لكل 16 بايت من الولاية كما فعلت عند تشفير الرسالة ، أي هو عكس نفسه. هذا يرجع إلى حقيقة أن منطق XOR يستخدم في العملية ، ويمكن تمثيل البايت في أرقام ثنائية.
يتم إضافة مفتاح الجولة الأخيرة (تلخيص) ببساطة إلى الرسالة المشفرة.
InvSubBytes. لم يتغير جوهر هذا التحول ، أي أن كل بايت من الرسالة التي يتم تحويلها يتم استبدالها بآخر مأخوذ من الجدول (S -1).-كتلة) استبدال. بالطبع ، جدول الاستبدال مختلف هنا. يتم استبدال البايت {x، y} بالبايت من Inv S (x، y) وفقًا لنفس المبدأ: x - صف الجدول ، y - عموده. يتم استرداد البايتة البديلة من الخلية عند تقاطع الصف (x) والعمود (y) من جدول Inv S (x، y).
كما كان من قبل ، حجم الجدول هو 16 × 16 = 256 بايت ، يتم الحصول على كل منها عن طريق الضرب والصفائح المتجهية (تحويل الألفة) من منتج ناقل التحول C. في الحقول الثنائية ، عمليات الجمع والطرح متكافئة ، لذلك يمكن ببساطة إضافة المتجه C إلى المنتج. يظهر الجدول InvSubBytes أدناه. العقدة المحددة للاستبدال S -1 معروضة في الجدول التالي 1 ، والقيم معطاة بالتنسيق الست عشري:
الجدول 1. جدول الاستبدالات للكتلة S -1 المعكوسة

يوضح الجدول أمثلة لاستبدال وحدتي بايت 4A → 5C و 9 F → 6E مليئة باللون الأخضر.
InvShiftRows. يغير هذا التحول الصفوف في الجدول (مربع الولاية) إلى اليمين (في الاتجاه المقابل للتحول الأصلي). تظل قيمة النقل لكل صف كما هي: لا يتم تغيير الصف الأول (العلوي) c0 = 0 ، ويتم إزاحة الثاني بمقدار c1 = 1 ، ويتم تحويل الصف التالي بواسطة c2 = 2 ، والصف الأخير هو c3 = 3 مواضع (خلايا). تم إعطاء القيم c0 و c1 و c2 و c3 في الجدول وفي الشكل السابق للجولة الأولى من تحويل الرسالة.

نتيجة هذا الضرب في التمثيل القياسي هي:
S'0C = ({0l} · S0C) ⊕ ({0b} · S1C) ⊕ ({0d} · S2C) ⊕ ({09} · S3C)؛
S'1C = ({09} S0C) ⊕ ({0l} S1C) ⊕ ({0b} S2C) ⊕ ({0d} S3C) ؛
S'2C = ({0d} S0C) ⊕ ({09} S1C) ⊕ ({0l} S2C) ⊕ ({0b} S3C) ؛
S'3C = ({0b} S0C) ⊕ ({0d} S1C) ⊕ ({09} S2C) ⊕ ({0l} S3C).
للحصول على تكنولوجيا المعلومات من أجهزة الكمبيوتر ، تستخدم خوارزمية فك التشفير نفس قيم المعلمات التي تم استخدامها في عملية التشفير. لتشكيل المفتاح الموسع ، تبقى القواعد كما هي.
خيار فك التشفير المباشر
خصوصيات خوارزمية فك التشفير لبعض التحولات العكسية تجعل من الممكن الحفاظ على نفس تسلسل العمليات كما هو الحال في خوارزمية التشفير ، ولكن بعض قيم المعلمات تتطلب تغييرات. بادئ ذي بدء ، نحن نتحدث عن المفتاح (تتكشف).
أظهر البحث أن ترتيب الدالتين SubBytes () و ShiftRows () لا يغير قيمة النتيجة ، أي أن هذه الوظائف قابلة للتبديل (وهي تتنقل). ينطبق هذا الموضع (الخاصية) أيضًا على الدالات InvSubBytes () و InvShiftRows (). من السهل شرح هذا النمط. النقطة هي أن كلا الوظيفتين تعملان على وحدات بايت صحيحة ، ويتم تنفيذ التحولات بواسطة عدد صحيح مضاعف من وحدات البايت ، ولا تغير قيمة وحدات البايت نفسها.
لاحظ ما يلي حول عملية MixColumns (). إنه خطي إلى بايت الإدخال (البيانات).
InvMixColumns (State XOR Round Key) = InvMixColumns (State) XOR
InvMixColumns (Key Round).
تسمح ميزات الوظائف (الخصائص) هذه بتغيير ترتيب تطبيقها ، أي
InvSubBytes (InvShiftRows ()) = InvShiftRows (InvSubBytes ()).
AddRoundKey (InvMixColumns ()) = InvMixColumns (AddRoundKey ()) ،
ولكن بشرط أن تكون الأعمدة (كلمات 32 بت) لمفتاح فك التشفير الموسع قد تم تمريرها مسبقًا من خلال وظيفة
InvMixColumns ().
ما سبق يعني أن طريقة فك تشفير الكمبيوتر يمكن أن تكون فعالة من خلال الحفاظ على ترتيب استخدام الوظائف المعتمدة للتشفير. من الواضح ، في هذه الحالة ، يتم تخفيض تكاليف تنفيذ الأجهزة والبرمجيات بشكل كبير. تتعلق التغييرات فقط الإجراء لتوليد نشر المفتاح.
في دالة InvMixColumns () ، تحتاج إلى تحويل نوع المتغير ، ومعلمة الإدخال للدالة هي صفيف بايت ثنائي الأبعاد (مربع) ، ويتم تشكيل المفتاح الموسع كمصفوفة خطية (سلسلة) من كلمات 32 بت. لهذا السبب ، من الضروري إجراء مطابقة النوع مع المربع.
دعونا نظهر ، باستخدام مثال التحول من جولتين ، نسختين متكافئتين من إجراء فك تشفير RIJNDAEL. الخيار الأول هو معكوس وظيفة التشفير المعتاد. يتم الحصول على الخيار الثاني من الأول عن طريق تغيير ترتيب العمليات في ثلاثة أزواج من التحويلات
InvShi ftRows () → InvSubBytes () مرتين و
AddRoundKey () → InvMixColumns () 1 مرة.
يتم حفظ نتيجة التحويل عند الانتقال من الأصل إلى
التسلسل العكسي للعمليات في الأزواج المحددة.
من الجدول نرى أن إجراء التشفير والمتغير الثاني لإجراء فك التشفير يتطابقان مع ترتيب استخدام المفاتيح المستديرة (عند تنفيذ عمليات AddRoundKey) والجداول البديلة (عند تنفيذ عمليات SubBytes () و InvSubBytes ()) ومصفوفات التحويل (عند تنفيذ MixColumns ( ) و InvMixColumns ()).
الجدول 2 - تسلسل التحولات في إصدار جولتين من RIJNDAEL

وتبين نتيجة مماثلة أنها صحيحة لأي عدد من الجولات.
استعادة مفتاح التشفير باستخدام المفتاح الفرعي الأخير
توليد مفاتيح التشفير AES المستديرة. الجدول الزمني الرئيسي لتوليد مفاتيح دائرية من مفتاح تشفير أصلي 128 بت هو وظيفة عودية. تتم مناقشة هذه الوظيفة بالتفصيل هنا . الشروط الأولية لإطلاقه هي الكلمات 4 4 بايت الأولى للمفتاح (الكلمات 4 × 32 بت) ، أي W [0] ، W [1] ، W [2] ، W [3].
دعونا نقوم بصياغة مشكلة استعادة مفتاح التشفير 128 بت هذا كالتالي: دع مكونات مفتاح الجولة المستديرة 10 W [43] ، W [42] ، W [41] ، W [40].
يلزم استرداد مفتاح التشفير الكامل باستخدام هذا المفتاح الدائري فقط.
من المناسب النظر في حل المشكلة أولاً على البيانات العددية. لنأخذ المثال الرقمي الوارد في FIPS PUB 197 كأساس.... يحتوي الجدول 3 على مفتاح الجولة 10.
يتم تنظيم إجراء توليد المفاتيح المستديرة بطريقة توفر حركة أمامية (تتكشف المفتاح) إلى جانب عدد من قيم المفاتيح السابقة. للانتقال للخلف من نقطة ما من سلسلة من القيم ، من الضروري الحصول على البيانات الأولية لعملية الحساب في هذه النقطة من العودة. دع نقطة العودة تكون الخطوة الأخيرة من الجولة العاشرة الأخيرة ، أي أربع كلمات من 4 بايت من مفتاح الجولة العاشرة Nk = Nb = 4 معروفة.
الجدول 3 - مفتاح 128 بت من الجولة العاشرة من تشفير AES

علاوة على ذلك ، يتم وضع نتائج وإجراءات خوارزمية الاسترداد الرئيسية الراحة في الجدول 4 ، والذي يشبه جدول توليد المفاتيح (المنقلب).
الجدول 4 - استعادة مفتاح التشفير من المفتاح المعروف للجولة العاشرة

شرح للجدول 4. يتم حساب الأعداد التقريبية بترتيب عكسي من العاشر إلى الأول. تحتوي ثلاثة أعمدة (3 ، 8 ، 9) من الجدول على مفاتيح جاهزة بأرقام حالية مختلفة اعتمادًا على رقم السطر i. تحتوي الخلايا المتبقية على بيانات مساعدة للحسابات المتوسطة. وبالتالي ، تظهر قيمة المفتاح W [i] في الجدول ثلاث مرات في ثلاثة أعمدة.
العمودان 1 و 2 هما الرقم r للجولة والرقم الترتيبي i للكلمة الرئيسية المكونة من 4 بايت. آخر كلمة من هذا القبيل أثناء التشفير لها الرقم i = 43. في الجدول نكتبها في السطر العلوي من العمود (9) الأيمن. الأرقام i من صفوف الجدول في تناقص وفي العمود 9 تتوافق مع كلمات المفتاح W [i]. يحتوي العمود الثامن على الكلمة W [i - Nk] للمفتاح بعدد مخفض W [43 - 4] = W [39] ، والعمود الثالث - الكلمة الرئيسية W [i - 1] = W [42] ، السابق W [i] = W [43].
معنى كلمة W [39] في العمود الثامن غير معروف ونجدها من البيانات الأولية باستخدام الصيغة:
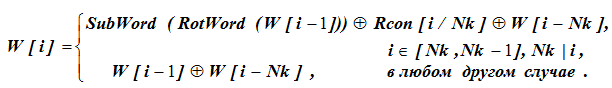
بالنسبة لحسابات الصيغة ، يتم التحقق أولاً من شروط تحديد سطر الصيغة. بالنسبة إلى W [43] و i = 43 و Nk لا تقسم القيمة 43 تمامًا ، أي بالنسبة لـ i = 43 ، يتم تحديد قيمة W [i] من خلال الخط السفلي للصيغة: W [43] = W [42] W [39]. هنا ، بالنسبة لقيم W [42] و W [43] ، لم يتم تعريف المصطلح الأخير W [39].
ثم W [39] = W [43] W [42] = b6630ca6 - e13f0cc8.
في العمليات الحسابية الثنائية mod2 ، تكون عمليات الجمع والطرح متكافئة ، لذا فإن حسابات البت لكل 4 بايت من الكلمة الرئيسية W [39] تأخذ الشكل (الجدول 5):
الجدول 5 - حسابات بايت للكلمة الرئيسية W [39].

وبالتالي ، تم العثور على قيمة الكلمة الرئيسية W [39] = 575c006e. ننقل هذه القيمة إلى العمود الثالث ، إلى الصف i = 40 وإلى العمود التاسع إلى
الصف i = 39. ويتم إجراء العمليات الحسابية في الصف i = 40 كما هو الحال عند توسيع المفتاح.
يجب تحديد الكلمة غير المعروفة W [i - Nk] = W [40 –Nk] = W [i = 36] كما في الحالة السابقة عن طريق الاختلاف W [36] = W [40] 7 عمود من السطر 40.
وفي المقابل ، القيمة في 7 يتكون العمود العشر من السطر 40 من مجموع العمودين الخامس والسادس. يتم الحصول على قيمة العمود الخامس من W [39] بعد التحول الدوري لـ RotWord (العمود الرابع) وعملية استبدال كلمة فرعية (العمود الخامس).
تأخذ نتائج هذه الإجراءات الشكل
RotWord (575c006e) = 5c006e57 ؛ Subword (5c006e57) = 4a639f5b.
يتم الحصول على القيمة في العمود السادس كثابت
Rcon [j = i / Nk] = Rcon [j = 40/4] = 2 j-1 = 2 9 .
يتم تمثيل هذا الثابت بواسطة بايت سداسي عشري
2 9 ≈100000000 = x 9 ، ولكن لا يوجد مثل هذا البايت في حقل GF (2 8 ): تحتاج إلى إيجاد ما تبقى من القسمة بواسطة كثيرات الحدود غير القابلة للاختزال ، أي.
بعد تضمين الثابت في الكلمة الرئيسية ، لدينا
Rcon [j = 40 / Nk] = 36000000 (العمود السادس). يتم الحصول على قيمة العمود السابع على أنها (العمود السابع) = (العمود الخامس) ⊕ (العمود السادس) = 4a639f5b⊕36000000 = 7c639f5b.
وأخيرًا ، بالنسبة لـ
W [36] = W [40] (العمود السابع من الصف 40) = d014f9a8 7c639f5b = ac7766f3.
مزيد من الحسابات عن طريق القياس تؤدي إلى النتيجة النهائية - مفتاح التشفير.
هناك المزيد من المعلومات حول وظائف w و RotWord و Rcon و SubWord. لنفترض أننا أشرنا إلى Kr [j] - البايت j للمفتاح المستدير r و w [i] كما هو الحال في الوثائق.
نحصل على: Kr = (w [Nk ∙ r]، w [Nk ∙ r + 1]، · · ·، w [Nk ∙ r + Nk - 1]).
بالنسبة إلى i مختلفة ، لدينا العلاقات التالية
لـ i ≠ 0 mod Nk و Nk ≤ i <Nb ∙ (Nr +1) و w [i] = w [i - Nk] xor w [i - 1] و
for i = 0 mod Nk، w [i] = w [i - Nk] xor SubWord (RotWord (w [i - 1])) xorRcon [i / Nk].
لذلك ، بالنسبة إلى i ≠ 0modNk و Nk 0≤i <Nb ∙ (Nr + 1) –Nk، w [i] = w [i + Nk] xor w [i + Nk - 1] ول i = 0modNk، w [i] = w [i + Nk] xorSubWord (RotWord (w [i + Nk - 1])) xorRcon [i + Nk / Nk]
مع AES-256 ، تحتاج إلى إضافة عملية كلمة فرعية عندما تكون قابلة للمقارنة بـ 4mod Nk. لذلك من الممكن استنتاج المفتاح السابق من المفتاح الفرعي النهائي والحصول خطوة بخطوة على القيمة K0 لمفتاح التشفير.
الأسس الرياضية للشفرات AES-128 كاملة ومفصلة هنا .
دعونا ننتقل إلى رسم الخرائط الميدانية ℓ: GF (2 8 ) → GF (2 8 )؛ x → x 2 + x. صورة هذه الخريطة
1 = Im (l) ذات أبعاد خافتة GF (2) (1) = 7.
المعادلة x2 + x = θ ، حيث θ 1 له حلان مختلفان (جذور المعادلة) 1 ، 2є GF (2 8 ).
بواسطة نظرية وايث h1⊕h2 = 1 ، يكون مجموع الجذور مساويًا لمعامل المعادلة لـ x 2 بعلامة معاكسة ، وناتج الجذور h1⊗h2 = θ يساوي الحد الثابت للمعادلة (في هذه المعادلة مع العلامة المعاكسة).
من المعروف أن عمليات الجمع والطرح للعناصر mod2 متكافئة في حساب الحقول الثنائية.

وبالتالي ، ترتبط جذور المعادلة بنسبة x2 = x1⊕1 ، حيث أن المعامل عند x في المعادلة هو 1. وهذا يعني أنه في التمثيل العشري لعناصر المجال بترتيبها المعجمي ، فإنها تقع واحدة تلو الأخرى ، وتختلف واحدًا تلو الآخر.
لذا بالنسبة لـ x = 0 و x = 1 وبالنسبة لـ x = 2 و x = 3 نحصل على:

نتائج (صور) التعيين في أزواج مخفضة (0 ، 1) ؛ (2 ، 3) تزامنت تمامًا ، أي نوعان يتوافقان مع صورة واحدة. وبالتالي ، فإن أصالة الصورة هي مرتين أقل من أصالة الصورة المسبقة وأبعادها من عناصرها هي 7. يتم
تحديد نتاج أزواج من الجذور ، أي المصطلح الحر لمعادلة تربيعية بشكل ملائم من خلال تمثيل القوة لعناصر المجال (الصور المعكوسة). في هذه الحالة ، يتم تلخيص الأسس mod255 ، أي modulo ترتيب مجموعة الضرب من الحقل GF (2 8 ).