أذكر خوارزمية ديكسترا
خوارزمية ديكسترا هي واحدة من خوارزميات نظرية الرسم البياني الأكثر شعبية. يتم استخدامه للعثور على أقصر مسار بين العقد على رسم بياني موجه. سنبدأ بالعقدة الأصلية وأطوال الحواف المعروفة بين العقد.
أولاً ، نقوم بتعيين قيمة المسافة من المصدر إلى جميع العقد. العقدة s تحصل على القيمة 0 لأنها المصدر ؛ البقية تحصل على قيم ∞ لتبدأ بها.
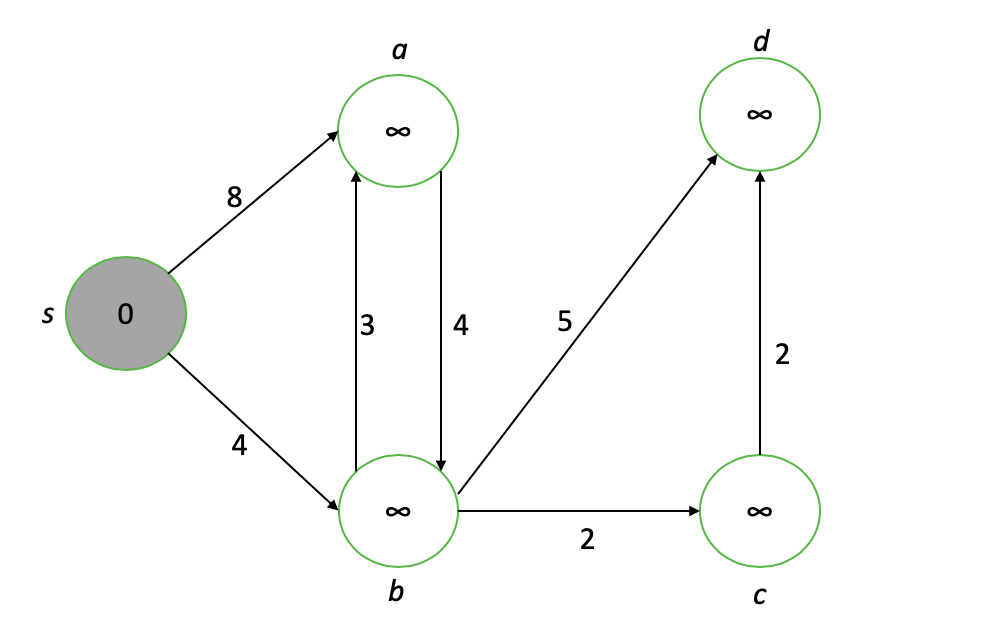
عقدة اهتمامنا هي العقدة الخام ذات القيمة الأقل (كما هو موضح باللون الرمادي) ، أي s. أولاً ، "نقوم بإضعاف" كل قمة متجاورة إلى عقدة الاهتمام الخاصة بنا ، وتحديث قيمهم إلى الحد الأدنى لقيمتها الحالية أو قيمة العقدة ذات الاهتمام بالإضافة إلى طول حافة الاتصال ...
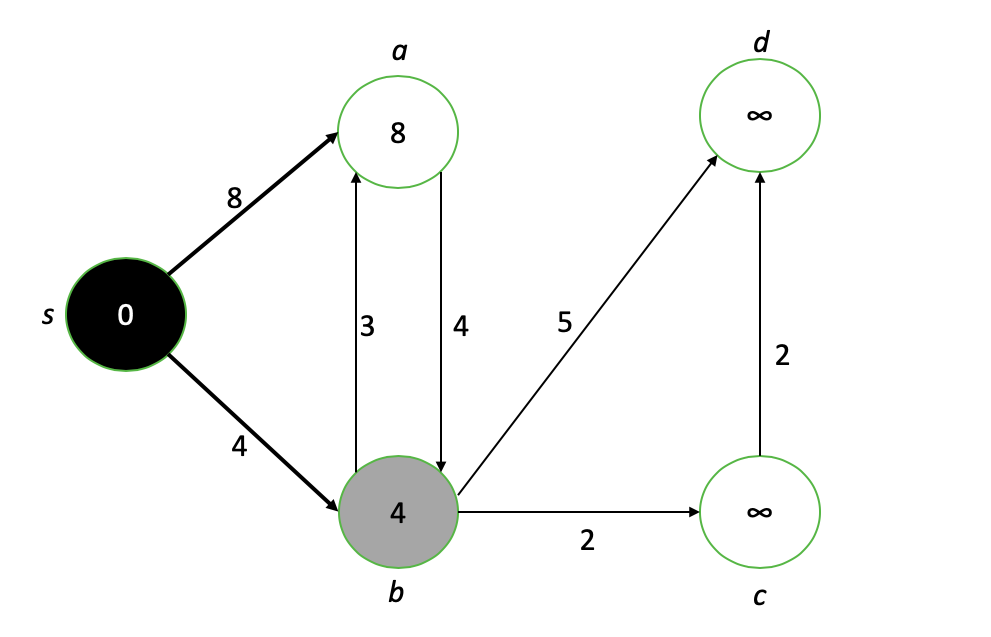
العقدة s مكتملة الآن (أسود) ، وجيرانها أ و ب لديهم قيمهم الجديدة. العقدة الجديدة ذات الاهتمام هي b ، لذا نكرر عملية "إضعاف" جيران b ووضع اللمسات الأخيرة على أقصر قيمة لمسار b.

بعد المرور عبر كل عقدة ، سنحصل أخيرًا على رسم بياني يوضح أقصر طول للمسار من المصدر إلى كل عقدة.
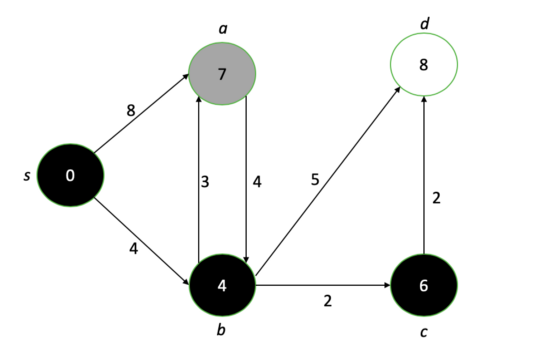


مخططنا النهائي بعد تشغيل خوارزمية ديكسترا. تمثل الأرقام في كل عقدة أقصر مسافة ممكنة من العقدة الأصلية.
تصور صور متاهة

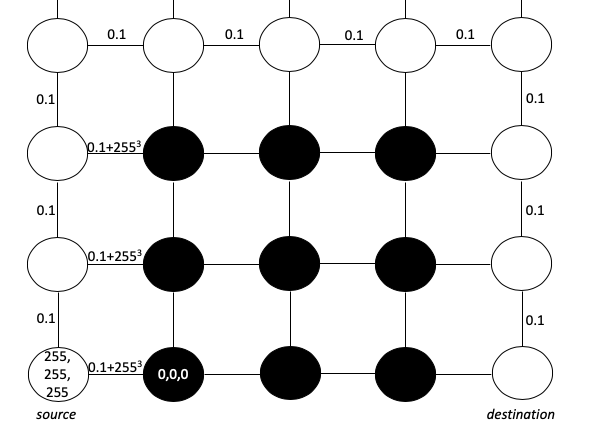
يمكننا أن نتخيل الصورة كمصفوفة من البكسل. كل بكسل (للبساطة) له قيمة RGB 0،0،0 (أسود) أو 255،255،255 (أبيض). هدفنا هو إنشاء مسار أقصر يبدأ باللون الأبيض ولا يعبر إلى الحدود السوداء. لتمثيل هذا الهدف ، يمكننا التعامل مع كل بكسل كعقدة ورسم حواف بين وحدات البكسل المتجاورة مع أطوال الحواف بناءً على الاختلاف في قيم RGB. سنستخدم صيغة Euclidean للمسافة المربعة ونضيف 0.1 لضمان عدم وجود طول مسار 0 - (وهو شرط لخوارزمية Dijkstra):
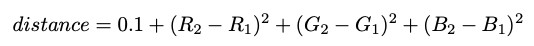
تجعل هذه الصيغة مسافة التقاطع عبر حدود المتاهة كبيرة للغاية. كما نرى ، فإن أقصر مسار من المصدر إلى الوجهة سيمر بوضوح حول الحاجز وليس من خلاله.
التنفيذ
يمكننا استخدام OpenCV ، مكتبة رؤية الكمبيوتر الشائعة لـ Python ، لاستخراج قيم البكسل وعرض صورنا المتاهة. دعونا أيضا تحديد إحداثيات مواقع البداية والنهاية من خلال إضافة نقاط إلى متاهتنا
import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread('maze.png') # read an image from a file using
cv2.circle(img,(5,220), 3, (255,0,0), -1) # add a circle at (5, 220)
cv2.circle(img, (25,5), 3, (0,0,255), -1) # add a circle at (5,5)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image
plt.show()
نقوم بإنشاء فئة Vertex التي ستساعدنا في تتبع الإحداثيات. نريد أيضًا تتبع العقدة الأصلية حتى نتمكن من إعادة بناء المسار بالكامل بمجرد العثور على قيم المسافة.
class Vertex:
def __init__(self,x_coord,y_coord):
self.x=x_coord
self.y=y_coord
self.d=float('inf') #current distance from source node
self.parent_x=None
self.parent_y=None
self.processed=False
self.index_in_queue=Noneنحتاج إلى إنشاء مصفوفة قمة تمثل الترتيب الثنائي الأبعاد لوحدات البكسل في الصورة. سيكون هذا هو الأساس لخوارزمية ديكسترا. نحافظ أيضًا على قائمة انتظار منخفضة الأولوية لتتبع العقد غير المعالجة.
def find_shortest_path(img,src,dst):
pq=[] #min-heap priority queue
imagerows,imagecols=img.shape[0],img.shape[1]
matrix = np.full((imagerows, imagecols), None)
#access matrix elements by matrix[row][col]
#fill matrix with vertices
for r in range(imagerows):
for c in range(imagecols):
matrix[r][c]=Vertex(c,r)
matrix[r][c].index_in_queue=len(pq)
pq.append(matrix[r][c])
#set source distance value to 0
matrix[source_y][source_x].d=0
#maintain min-heap invariant (minimum d Vertex at list index 0)
pq = bubble_up(pq, matrix[source_y][source_x].index_in_queue)نحتاج إلى بعض الوظائف المساعدة لمساعدتنا في العثور على الحواف وطول الحواف بين القمم:
#Implement euclidean squared distance formula
def get_distance(img,u,v):
return 0.1 + (float(img[v][0])-float(img[u][0]))**2+(float(img[v][1])-float(img[u][1]))**2+(float(img[v][2])-float(img[u][2]))**2
#Return neighbor directly above, below, right, and left
def get_neighbors(mat,r,c):
shape=mat.shape
neighbors=[]
#ensure neighbors are within image boundaries
if r > 0 and not mat[r-1][c].processed:
neighbors.append(mat[r-1][c])
if r < shape[0] - 1 and not mat[r+1][c].processed:
neighbors.append(mat[r+1][c])
if c > 0 and not mat[r][c-1].processed:
neighbors.append(mat[r][c-1])
if c < shape[1] - 1 and not mat[r][c+1].processed:
neighbors.append(mat[r][c+1])
return neighborsيمكننا الآن تنفيذ خوارزمية Dijkstra وتعيين قيم المسافة (د) لجميع رؤوس وحدات البكسل في صورة المتاهة:
while len(pq) > 0:
u=pq[0] #smallest-value unprocessed node
#remove node of interest from the queue
pq[0]=pq[-1]
pq[0].index_in_queue=0
pq.pop()
pq=bubble_down(pq,0) #min-heap function, see source code
u.processed=True
neighbors = get_neighbors(matrix,u.y,u.x)
for v in neighbors:
dist=get_distance(img,(u.y,u.x),(v.y,v.x))
if u.d + dist < v.d:
v.d = u.d+dist
v.parent_x=u.x #keep track of the shortest path
v.parent_y=u.y
idx=v.index_in_queue
pq=bubble_down(pq,idx)
pq=bubble_up(pq,idx)الآن يمكننا استدعاء أقصر وظيفة للمسار ورسم الحل في متاهتنا:
img = cv2.imread('maze.png') # read an image from a file using opencv (cv2) library
p = find_shortest_path(img, (25,5), (5,220))
drawPath(img,p)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image on the screen
plt.show()

لنجرب متاهات أخرى من جميع أنحاء الإنترنت.

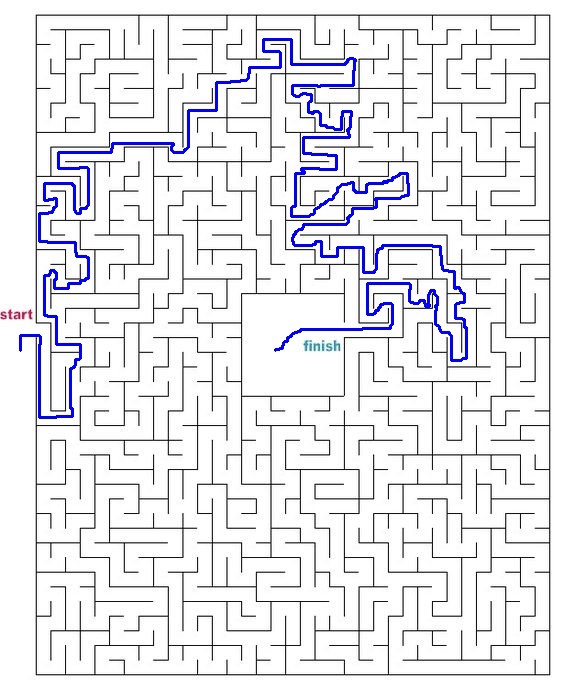


الكود المصدري الكامل متاح على GitHub هنا .
تابع: Python Learning Project: 40 Lines of Code Interface (Part 2)

تعرف على تفاصيل كيفية الحصول على مهنة رفيعة المستوى من نقطة الصفر أو المستوى الأعلى في المهارات والمرتبات من خلال أخذ دورات SkillFactory المدفوعة عبر الإنترنت:
- دورة تعلم الآلة (12 أسبوعًا)
- تدريب مهنة علوم البيانات من الصفر (12 شهرًا)
- مهنة التحليلات مع أي مستوى بداية (9 أشهر)
- «Python -» (9 )