🎆 💒 ⚡️ AES هو معيار التشفير الأمريكي. الجزء الخامس. الهجوم ♌️ ☝️ 🏊

مقالات أخرى في الدورة

AES — . I

ES — . II

AES — . III

AES — . IV

AES — . V.

بعد عرض تقديمي مفصل مع تفاصيل التحولات الفردية ، مع عناصر محدودة ، وليست مجردة (كما هو الحال في العديد من المنشورات ، وليس باستثناء حقل Khabrovsky) ، ولكن ( ملموس ) ، يتم من خلاله تنفيذ RIJNDAEL و AES-128 و ( تنفيذ عمليات معيار AES-128 ) ، يمكننا الانتقال إلى دراسة الهجمات المحتملة على التشفير. في الوقت الحالي ، سنقتصر على هجوم واحد ، في رأينا ، هو هجوم هبر الأكثر قابلية للفهم والشفافية (على الرغم من أنه ربما ليس لجميع القراء).

لقد تعودت بالفعل على المساوئ ، لكن ما لا يمزح به الشيطان. تم إجراء تحليل للهجمات المحتملة والنتائج المتوقعة من قبل العديد من المؤلفين ، لكن من الواضح أن الأمثلة الناجحة الملموسة أو التصاميم الرائعة ببساطة ليست كافية. هنا سننظر من وجهة نظر رياضية في هجوم باستخدام خطأ أدخله الدخيل في النص المشفر. عند اختيار هجوم لمظاهرة ، حاول المؤلف عدم إشراك أولئك الذين يستخدمون أشياء رياضية ملتوية وغامضة للغاية ، لكن الموضوع المعني نفسه خطير للغاية ولا يسمح بالانتقال إلى التفسيرات على "الأصابع".

يتمثل أحد الأغراض المهمة للنشر في إظهار تطبيق الرياضيات ، الذي يشكل أساس AES-128 ، والذي ، للأسف ، يتجاهل العديد من المؤلفين أو يفسرون خطأ لا أساس له من الصحة ولا أساس له ، مسترشدين بحقيقة أن قلة من الناس يمكنهم التحقق من اختراعاتهم والإشارة إليها.

مادة المقال ليست بالكامل المفهوم الأصلي للهجوم ، الإجراءات الرئيسية مأخوذة من العمل ، لكن تم إعدادها بعناية واستكمالها واختبارها تجريبياً من قبل طلابي. لقد حصلوا على تدريب جيد في كل من الجبر العالي وعلم التشفير.

1. هجوم على مفتاح تشفير AES

أولاً ، يتم وصف هجوم على AES في حالة بسيطة ، ثم يتضح بعد ذلك كيف يمكن تعميم مثل هذا الهجوم. الهدف من الهجوم قيد النظر هو استعادة مفتاح K (Nr) من التشفير. بمجرد تحديد المفتاح الجزئي (الدائري) K (Nr) ، يصبح من السهل الحصول على المفتاح K.

1.1 مبدأ الهجوم

يُفترض أنه من الممكن التغيير عن طريق إدخال الخطأ "" في بايت منفصل من المصفوفة S للحالة (واحدة من 16) بعد عملية ShiftRows (Nr - 1) ، أي الجولة قبل الأخيرة ، والفهرس (# من الخلية) للبايت التالف (عنصر ) حالة. يمكن حذف هذه الفرضية الأخيرة ؛ تم تقديمها من أجل شرح آلية الهجوم بسهولة أكبر. من المفترض أن تكون القيمة الجديدة لعنصر الحالة غير معروفة.

لا يمتد الخطأ "ε" إلى أكثر من أربعة بايت من حالة الخروج من العملية. لجميع العناصر الأربعة المتغيرة لحالة الإخراج ، تم العثور على مجموعة من القيم (مجموعة) من نواقل الخطأ المحتمل "" في القسم 1.4. بالإضافة إلى ذلك ، يصبح من الممكن تقاطع مجموعات القيم الممكنة "" (التعريف 1) لهذه العناصر الأربعة. عندما تتقاطع هذه المجموعات ، يتم الحصول على مجموعة أصغر ، وبالتالي يتم تقليل عدد النصوص المشفرة المطلوبة للتحليل الكامل.

أخيرًا ، لكل خطأ ، نقوم بطباعة بعض القيم المشوهة المحتملة للعناصر الأربعة للمفتاح الدائري السابق. بتكوين نصوص مشفرة أخرى ، نجد أربعة بايت من المفتاح الدائري K (10). يظل هذا الهجوم ناجحًا حتى مع وجود الكثير من الافتراضات العامة حول موقع الخطأ. مثل نقص المعلومات حول موقع الخطأ قبل التحويل التاسع MixColumns (). سيكشف الفرق بين مصفوفة نص التشفير مع وبدون تشوهات التشوهات وموضعها (في المثال ، هذه المواقف 0،7،10،13).

يُقترح أيضًا أن أخطاء "" التي تم تقديمها في الجولة 8 (قبل تحويل الأعمدة المختلطة الثامن ()) يمكن أن تكون مفيدة في التحليل. ولكن في الوقت نفسه ، يزداد عدد نصوص التشفير المطلوبة لتحليل أكثر اكتمالاً. بالنسبة للمثال العددي قيد الدراسة ، هناك حاجة إلى حوالي عشرة نصوص مشفرة للحصول على أربعة بايت من المفتاح الدائري K (10) ، في ظل ظروف لا تؤخذ فيها في الاعتبار فرضية مواقع الخطأ.

1.2 مثال رقمي لتأثير خطأ على رسالة

هنا يتم استخدام نفس المثال على النحو الوارد في ملحق العمل المسمى . يتم النظر في الجولتين قبل الأخيرة والأخيرة من عملية التشفير (تمثيل بايت البيانات له الشكل):

الإدخال = '32 43 F6 A8 88 5A 30 8D 31 31 98 A2 E0 37 07 34 '؛

مفتاح التشفير = '2B 7E 15 16 28 AE D2 A6 AB F7 15 88 09 CF 4F 3C' ؛

الإخراج = '39 25 84 1D 02 DC 09 FB DC 11 85 97 19 6A 0B 32 '؛

خطأ "ε" = '1E 00 00 00 00 00 00 00 00 00 00 00 00'.

يوضح الرسم البياني التالي القيم الموجودة في مصفوفات الحالة وفقًا لطول كتلة التشفير وطول مفتاح التشفير البالغ 16 بايت لكل منهما (أي ، Nb = 4 و Nk = 4).

يتم عرض انتشار الخطأ بالتدوين الغامق والسداسي العشري. فيما يلي مربعات الدولة في المواقف المختلفة:

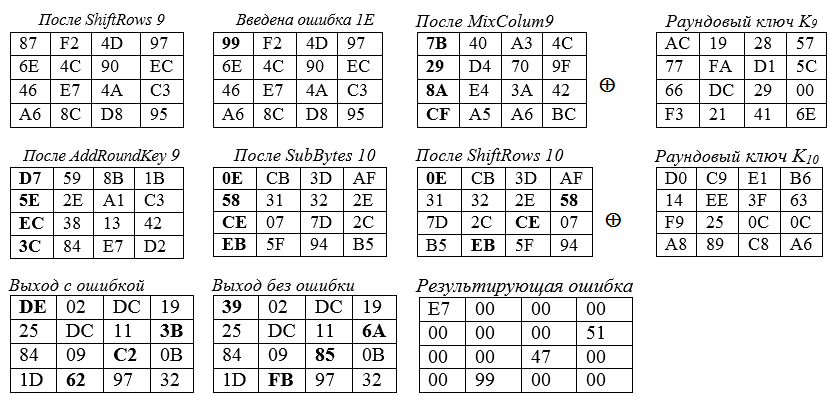
الخطأ "ε" = 1E ، المدرج في البايت 0 من حالة الجولة التاسعة ، ينتج عنه تغييرات في البايتات الأربعة للحالة النهائية. أمثلة على حسابات خلايا الزاوية للقطر الرئيسي لـ "مربع" الحالة:

- الخطأ "ε" = 1E

87 ⊕ 1E = 1000 0111⊕ 0001 1110 = 1001 1001 = 99

تم إدخالها في الخلية اليسرى العلوية (الزاوية) لمربع الولاية للدور التاسع - أسفل اليمين يتم تلخيص حالة زاوية الجولة التاسعة بعد MixColum9 بالبايت الرئيسي K (9):

BC ⊕ 6E = 1011 1100⊕ 0110 1110 = 1101 0010 = d2.

- حساب قيم الخطأ الناتج.

في حالة وجود نصين للرسالة بهما خطأ وبدون أخطاء ، يتم تحديد قيم ومواضع وحدات بايت الحالة التالفة بطرح نص واحد من الآخر. في حالتنا ، يمكن استبدال هذا الطرح بجمع النصوص بالوحدة الثانية. نحصل على نتيجة غير صفرية فقط للبايتات التي تم تغييرها بواسطة خطأ تم إدخاله في النص المصدر.

على سبيل المثال ، في شكل سداسي عشري ، نجد قيم الخطأ:

الجدول 7 - حساب قيم الخطأ

نتيجة لذلك ، أخطاء الاختلاف

ε_{0}^{'} = E 7, ε_{1}^{'} = 51, ε_{2}^{'} = 47, ε_{3}^{'} = 99

$ε_0’=E7, ε_1’=51, ε_2’=47, ε_3’=99$ ... دعنا نعطي مثالاً لحساب بايت الخطأ الأخير:

62 ⊕ FB = 01100010 ⊕11111011 = 1001 1001 = 99.

تغيرت مواضع بايت الحالة بسبب الخطأ

ε_{0}^{'} = E 7, ε_{1}^{'} = 51, ε_{2}^{'} = 47, ε_{3}^{'} = 99

$ε_0’=E7, ε_1’=51, ε_2’=47, ε_3’=99$ . تشير إلى مؤشرات عناصر المفتاح الدائري (الجولة الأخيرة) ، مثل K [0] ، K [7] ، K [10] ، K [13]. هنا ، 0 ، 7 ، 10 ، 13 هي أرقام خلايا مصفوفة الحالة ، والمصفوفة Ao هي مصفوفة التحويل لخلط أعمدة عملية التشفير ، العمود الأول منها على الشكل: '02' ، '01' ، '01' ، '03'.

كيف يؤثر الخطأ المحقون على الحالة النهائية

تحليل المعلومات التي تم الحصول عليها عند حدوث خطأ

العملية الوحيدة التي يمكن أن تحتوي على معلومات تتعلق بالمفتاح K (Nr) هي آخر تحويل SubBytes (). لذلك ، لدينا أربع معادلات ، حيث x0 ، x1 ، x2 ، x3 ، ε متغيرات غير معروفة.

نريد الحصول على حلول للمعادلات الأربع التالية:

s (x_{0} + 2 ε) + s (x_{0}) = ε_{0}^{'},

$s(x_0 +2ε) + s(x_0) =ε_0’,$

s (x_{1} + ε) + s (x_{1}) = ε_{1}^{'},

$s(x_1 +ε) + s(x_1) =ε_1’,$

s (x_{2} + ε) + s (x_{2}) = ε_{2}^{'},

$s(x_2 +ε) + s(x_2) =ε_2’,$

s (x_{3} + 3 ε) + s (x_{3}) = ε_{3}^{'},

$s(x_3 +3ε) + s(x_3) =ε_3’,$

بايت

ε_{0}^{'}, ε_{1}^{'}, ε_{2}^{'}, ε_{3}^{'}

$ε_0’, ε_1’, ε_2’, ε_3’$ تم تعديله بواسطة خطأ يحتوي على معلومات حول المفتاح غير المعروف الذي أنشأ هذه البايت.

يمكن تعميم كل هذه المعادلات في معادلة واحدة

s (x + cε) + s (x) = ε '، (1)

حيث القيمة الثابتة =' 01 'أو' 02 'أو' 03 'وهذه هي المعادلة التي سنحلها بشكل أكبر و تحليل.

التعريف 1 . مجموعة حلول المعادلة (1) للأخطاء ε يُرمز لها بالرمز B (cε ') ويتم تعريفها بالتعبير:

B (cε') = S (cε ') = {ε є GF [2 ⁸ ]: ∃ x є GF [2 ⁸ ] ، ث (س + جε) + ث (س) = ε '} ، | ب (جε') | = 127.

هذه منطقة خطأ فردية تقابل خطأ محدد '. بالنسبة إلى 'الأخرى ، ستكون مناطق الخطأ مختلفة.

التعريف 2 . النظر في تحويل خطي ℓ فوق الحقل GF (2):

ℓ: GF [2 ⁸ ] → GF [2 ⁸ ] ؛

س → س ² + س.

صورة ℓ عبارة عن تعيين لمساحة Im (ℓ) GF (2) - متجه ، أي ، مجموعة العناصر

(x ² + x) من GF [2 ⁸ ] نشير إلى 1 = Im (ℓ) وبعدها قاتم GF (2) (E1) = 7. إذا كانت θ є 1 ، فهناك حلان مختلفان x1 ، x2 є GF [ 2 ⁸ ] المعادلات x ² + x = θ ، والحلول تحقق العلاقة x2 = x1 + 1 و x2 ∙ x1 = θ (modd φx، (2 ⁸ -1)) بواسطة نظرية فييتا .

المتغير θ هو مصطلح مجاني في المعادلة التربيعية ،

دعونا نوضح التحويل الخطي المدروس بمثال.

مثال تم تعيين حقل GF [2 ⁸] ، يتم إجراء التحويل x → x ² + x على عناصرها .

الجدول 8 - الجزء الأولي من الحقل GF [2 ⁸ ] ونتائج تحول العناصر.

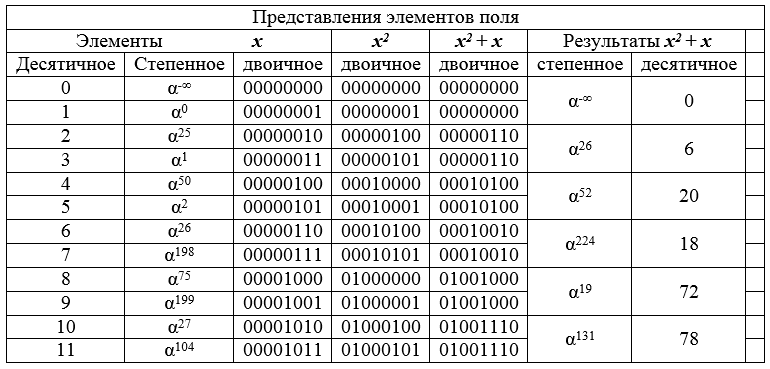
يوضح الجدول 8 كيف يغير التحويل الأزواج المجاورة في قائمة مرتبة عشرية إلى نفس عنصر الحقل. ويترتب على ذلك أن نتيجة التحويل (الصورة) أقل مرتين من الصورة السابقة (الحقل ، كما كان ، مضغوط مرتين). يشكل مبدأ تقلص أبعاد المجموعات أساس الهجوم المقترح.

الاقتراح 2 . العبارة التالية صحيحة لـ λ1، λ2 є GF [2 ⁸ ] - {0}:

2. التعميم والتنفيذ

بادئ ذي بدء ، باستخدام تطبيق برمجي خاص ، يتم إنشاء 20 نصًا مشفرًا بها خطأ. للقيام بذلك ، يتم إدخال النص المصدر والمفتاح والخطأ في النموذج (البرنامج) ويتم تعيين رقم الموضع الذي تم وضع الخطأ فيه. بالضغط على زر "ابدأ" ، يقوم البرنامج بتنفيذ الخوارزمية ويعرض نتائج جولتي التشفير الأخيرتين في شكل موسع للنص مع وجود خطأ ، ونص بدون خطأ ، والفرق بينهما. بعد ذلك ، يتم حفظ النص المشفر بدون خطأ وبخطأ. يتم تغيير قيمة الخطأ دوريًا وبالضغط على الزر "ابدأ" ، يتم الحصول على النص المشفر التالي مع وجود خطأ. على قيمة واحدة للعمود ، تم تكوين 5 نصوص مشفرة بها خطأ.

لتنفيذ الهجوم ، يجب فتح ملف به نص مشفر بدون خطأ ونص مشفر مع وجود خطأ في استخدام البرنامج (يتم تقديم البيانات في الملف في شكل سداسي عشري) ، يتم عرض النصوص المشفرة والفرق بينها كمصفوفة مربعة من البايت (الحالة). يؤدي الضغط على الزر "بحث عن مفتاح" إلى بدء إجراء البحث عن وحدات البايت الممكنة للمفتاح. يتم عرض الحالة الحالية للعمليات في مربع نص. بعد ذلك ، يتم فتح نص مشفر مع وجود خطأ آخر ، ويتم تكرار الإجراء. عند تلقي مستدير 10 بايت مفتاح ، فإنه يظهر أيضًا في صفيف بايت المربع المقابل. عند تشغيل جميع النصوص المشفرة العشرين التي تم إنشاؤها في المرحلة السابقة مع وجود خطأ ، هناك احتمال كبير للحصول على قيم جميع وحدات البايت الخاصة بمفتاح الجولة 10 (وإلا ، هناك حاجة أيضًا إلى نصوص مشفرة بها أخطاء).بعد ذلك ، قم باستعادة مفتاح التشفير وفقًا للخوارزمية "استرداد مفتاح التشفير باستخدام آخر مفتاح فرعي" المعطىهنا .

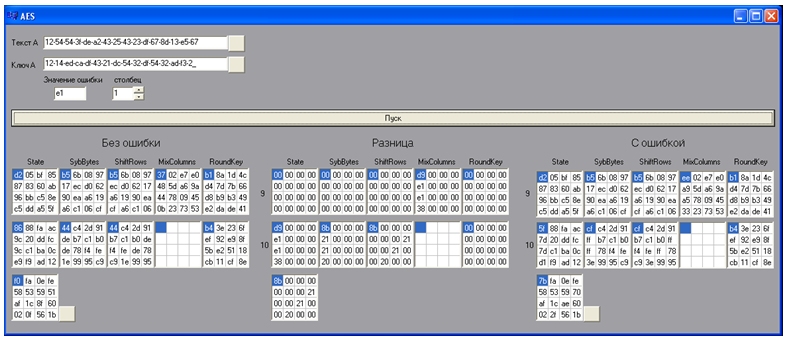
الشكل 11 - منتج برمجي لإنشاء نص مشفر به خطأ

لتسريع إجراء تعداد نصوص مشفرة مع وجود خطأ ، يمكنك وضع علامة أمام زر "البحث عن مفتاح"

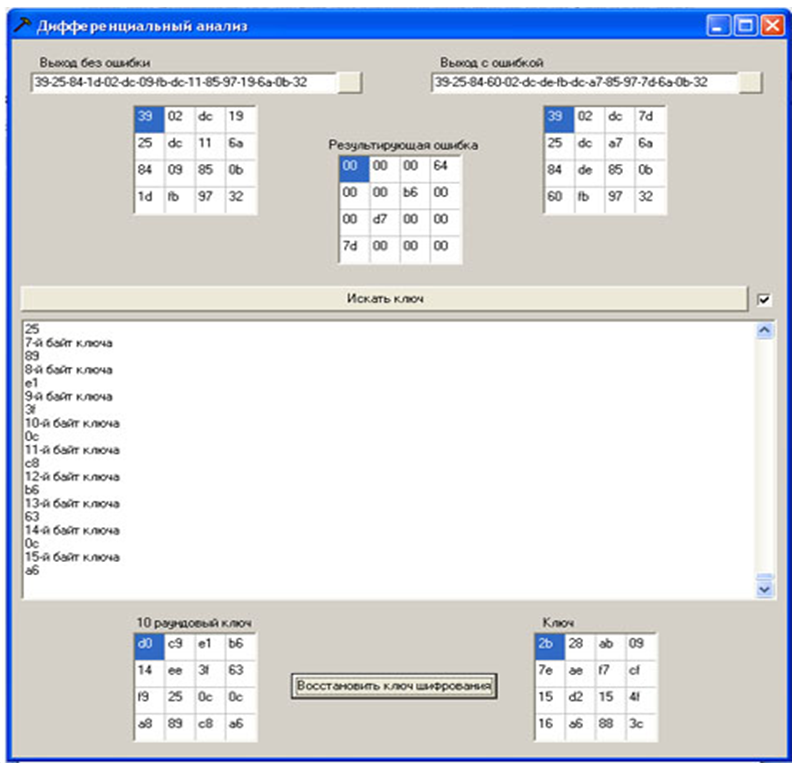
الشكل 12 - تنفيذ البرنامج للهجوم

مثال على منتج البرنامج:

كود المصدر 3243f6a8885a308d313198a2e0370734

المفتاح 2b7e151628aed2a6abf7158809cf4f3c

خطأ 1 1e000000000000000000000000000000

نص مجفر مع الخطأ 1

بايت ممكن de25841d0

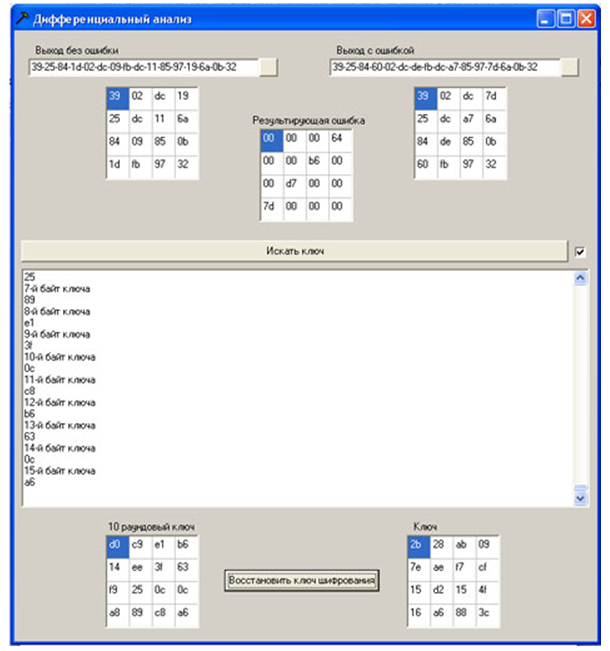
الشكل 13 - مثال على عملية البرنامج

جولة 10 مفتاح d014f9a8c9ee2589e13f0cc8b6630ca6 المفتاح المسترد بالكامل

2b7e151628aed2a6abf7158809cf4f3c ، كما هو متوقع ، يطابق المفتاح المحدد في جلسة التشفير.

2.1. الموقف عندما لا يكون هناك خطأ في معلومات الموقع

في هذه المرحلة ، يُفترض أن الخطأ موجود في بايت الحالة بين آخر عمليتي تنفيذ لعملية MixColumns. هذه هي الحالة نفسها ، باستثناء حقيقة أنه يمكن إحاطة الخطأ بين بايت من 1 إلى 16. يتم ضرب الخطأ في عملية MixColumns وينتشر إلى 4 بايت من الحالة.

يتم إنشاء خطأ إجباري في الصف الأول من مصفوفة الحالة التفاضلية. هنا من الممكن تحديد العمود الذي ينتمي إليه الخطأ الذي تم إدخاله من خلال النظر في عمود الخطأ القسري. يتم ذلك عن طريق فحص مواضع السطر الأربعة المحتملة للخطأ الذي تم إدخاله باستخدام الطريقة الموضحة في الوصف السابق.

2.2. جهاز الأجهزة

افترض أن لديك القدرة على التدخل فعليًا في جهاز AES. أولاً ، دعونا نحسب الأصفار لأكثر من عشرة نص عادي عشوائي باستخدام جهاز AES. ثم نقوم بتغيير مثال المشروع عن طريق قطع الخطوط وربطها بالأرض (أو Vcc) بشكل مؤقت بين بايتين خلال الجولة ، وتقع جولتان قبل الانتهاء. بعد كل شيء ، لدينا بايت في الجولة Nk -2 ، يتم استبداله دائمًا بـ "00" (أو "FF").

نحسب مرة أخرى نفس الرسالة مع جهاز التمثيل. بالنسبة للنص العادي العشوائي ، فإن البايت المعيب يشبه الخطأ العشوائي. يترجم هذا الخطأ الفردي إلى أربعة أخطاء في جولة Nk -1 وستة عشر خطأ في جولة Nk. في هذه الحالة ، يمكن الحصول على مصفوفة الانحراف (التفاضلية) ، والتي يمكن من خلالها ، من خلال تحليل الخطأ ، العثور على آخر مفتاح دائري.

الأدب:

[1] FIPS PUB 197: معيار التشفير المتقدم ، csrc.nist.gov/publications/fips/fips197/fips-197.pdf

[2] Boneh و DeMillo و Lipton ، حول أهمية فحص بروتوكولات التشفير للأخطاء ، ملاحظات محاضرة في علوم الكمبيوتر ، التقدم في علم التشفير ، وقائع EU-ROCRYPT'97 ، ص. 37-51 ، 1997.

[3] E. Biham & A. Shamir ، تحليل الأخطاء التفاضلية لأنظمة تشفير المفتاح السري ، CS 0910 ، Proceedings of Crypto'97.

[4] روس ج.أندرسون ، ماركوس جي كون: مقاومة العبث - ملاحظة تحذيرية ، ورشة عمل USENIX الثانية حول إجراءات التجارة الإلكترونية ، أوكلاند ، كاليفورنيا ، 18-21 نوفمبر ، 1996 ، ص 1-11 ، ISBN 1-880446- 83-9.

AES هو معيار التشفير الأمريكي. الجزء الخامس. الهجوم