😳 🌎 🔍 شبكات بايزي مع بايثون - ماذا ولماذا؟ 🛢️ 🏴󠁧󠁢󠁷󠁬󠁳󠁿 🌬️

تنويه: هذه المقالة ترجمة معدلة. يمكن قراءة الأصل هنا .

شبكات بايزي مع بيثون - شرح مع أمثلة

نظرًا لمحدودية المعلومات (خاصة باللغة الروسية الأصلية) وموارد العمل ، فإن شبكات بايزي محاطة بعدد من المشاكل. ويمكن للمرء أن ينام جيدًا إذا لم يتم تطبيقه في معظم التقنيات المتقدمة للعصر ، مثل الذكاء الاصطناعي والتعلم الآلي.

استنادًا إلى هذه الحقيقة ، تم تخصيص هذه المقالة تمامًا لعمل شبكات بايزي وكيف أنها لا تستطيع أن تشكل مشاكل ، ولكن يمكن تطبيقها في حلها ، حتى إذا كانت المشكلات التي يتم حلها مربكة للغاية.

هيكل المادة

ما هي شبكة بايزي؟
ما هي الرسوم البيانية الحلقية الموجهة؟
ما الرياضيات تكمن في شبكات بايزي
مثال يعكس فكرة شبكة بايزي
جوهر شبكة بايزي
شبكة بايزي في بيثون
تطبيق شبكات بايزي

لنذهب.

ما هي شبكة بايزي؟

تندرج شبكات بايزي في فئة النماذج الرسومية الاحتمالية (GPM). تستخدم VGMs لحساب التباين للتطبيق في مفاهيم الاحتمالية.

الاسم الشائع لشبكات Bayesian هو Deep Networks. يتم استخدامها لنمذجة الرسوم البيانية الحلقية الموجهة.

ما هي الرسوم البيانية الحلقية الموجهة؟

الرسم البياني الحلقي الموجه (مثل أي رسم بياني في الإحصائيات) هو هيكل من العقد والروابط ، حيث تكون العقد مسؤولة عن بعض القيم ، وتعكس الروابط العلاقات بين العقد.

الحلق == عدم وجود دورات موجهة. في سياق الرسوم البيانية ، يعني هذا الصفة أنه عند بدء مسار من نقطة واحدة ، فإننا لا نذهب من خلال الرسم البياني بأكمله للرسم البياني ، ولكن جزءًا منه فقط. (هذا ، على سبيل المثال ، إذا بدأنا من العقدة 2 في الصورة ، فلن نصل بالتأكيد إلى العقدة 1).

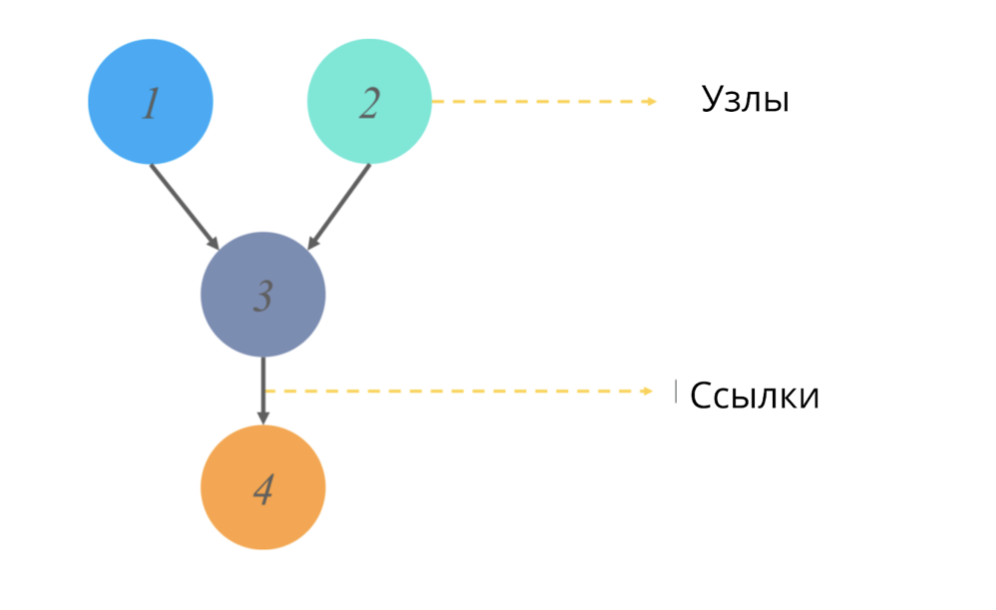
ما الذي تحاكيه هذه الرسوم البيانية وما قيمة المخرجات التي تعطيها؟

تستند نماذج الرسوم البيانية الموجهة غير المؤكدة أيضًا إلى تغيير في الأصل الاحتمالي لحدث ما لكل من القيم العشوائية. يمكن تطبيق جدول الاحتمالات الشرطية لتمثيل وتفسير كل قيمة ، وبالتالي يمكننا محاكاة تفرع احتمالية الأحداث المتسلسلة.

كل شيء جيد. أنا أيضا حصلت على الخلط في البداية. من أجل فهم أفضل ، دعنا نحلل المكون الرياضي لشبكات بايزي.

رياضيات شبكة بايزي

كما سبق ذكره في التعريف ، تقوم شبكات بايزي على نظرية الاحتمال ، لذلك ، قبل البدء في العمل مع شبكات بايزي ، يجب التعامل مع سؤالين:

ما هو الاحتمال المشروط؟

ما هو متوسط التوزيع الاحتمالي المشترك؟

الاحتمال

الشرطي الاحتمال الشرطي لحدث X هو القيمة العددية لاحتمال وقوع الحدث X ، بشرط أن يكون هناك حدث Y بالفعل.

الصيغة الاحتمالية القياسية لقيمة واحدة (غير معطاة في المقالة): P (X) = n (x) / N ، حيث n هي الأحداث قيد التحقيق ، و N كلها أحداث محتملة.

لقيمتين ، يتم تطبيق الصيغ التالية:

إذا كانت X و Y أحداثًا تابعة:

P (X أو Y) = P (X ⋂ Y) / P (Y) ، تقاطع احتمال X و Y / للاحتمال Y. (العلامة "في البسط تعني تقاطع الاحتمالات)

إذا كانت الأحداث X و Y مستقلة:

P (X) أو Y) = P (X) ، أي أن وقوع الأحداث قيد الدراسة متساوٍ على الأرجح.

الاحتمال المشترك الاحتمال

المشترك هو تعريف المقياس الإحصائي لحدثين أو أكثر في نفس الوقت. أي أن الأحداث X ، Y ، ولنفترض أن C تحدث معًا ونعكس الاحتمال التراكمي لها باستخدام القيمة P (X ⋂ Y ⋂ C).

كيف يعمل هذا في شبكات بايزي؟ لنلقي نظرة على مثال.

مثال يعكس جوهر شبكة بايزي

لنفترض أننا بحاجة إلى وضع نموذج لاحتمال الحصول على إحدى درجات درجات الطالب في الاختبار.

تتكون النتيجة من:

مستوى صعوبة الامتحان (هـ): متغير منفصل بتدرجين (صعب ، سهل)
معدل ذكاء الطالب: متغير منفصل بتدرجين (منخفض ، مرتفع)

سيتم استخدام قيمة التقييم الناتجة كمتنبئ (القيمة التنبؤية) لاحتمال دخول الطالب أو الطالبة إلى الجامعة.

ومع ذلك ، فإن متغير الذكاء سيؤثر أيضًا على القبول في القبول.

نحن نمثل جميع القيم باستخدام رسم بياني لا دوري موجه وجدول توزيع احتمالي مشروط.

باستخدام هذا التمثيل ، يمكننا حساب بعض الاحتمالات التراكمية ، التي تشكلت من ناتج الاحتمالات الشرطية لخمسة متغيرات.

الاحتمال التراكمي:

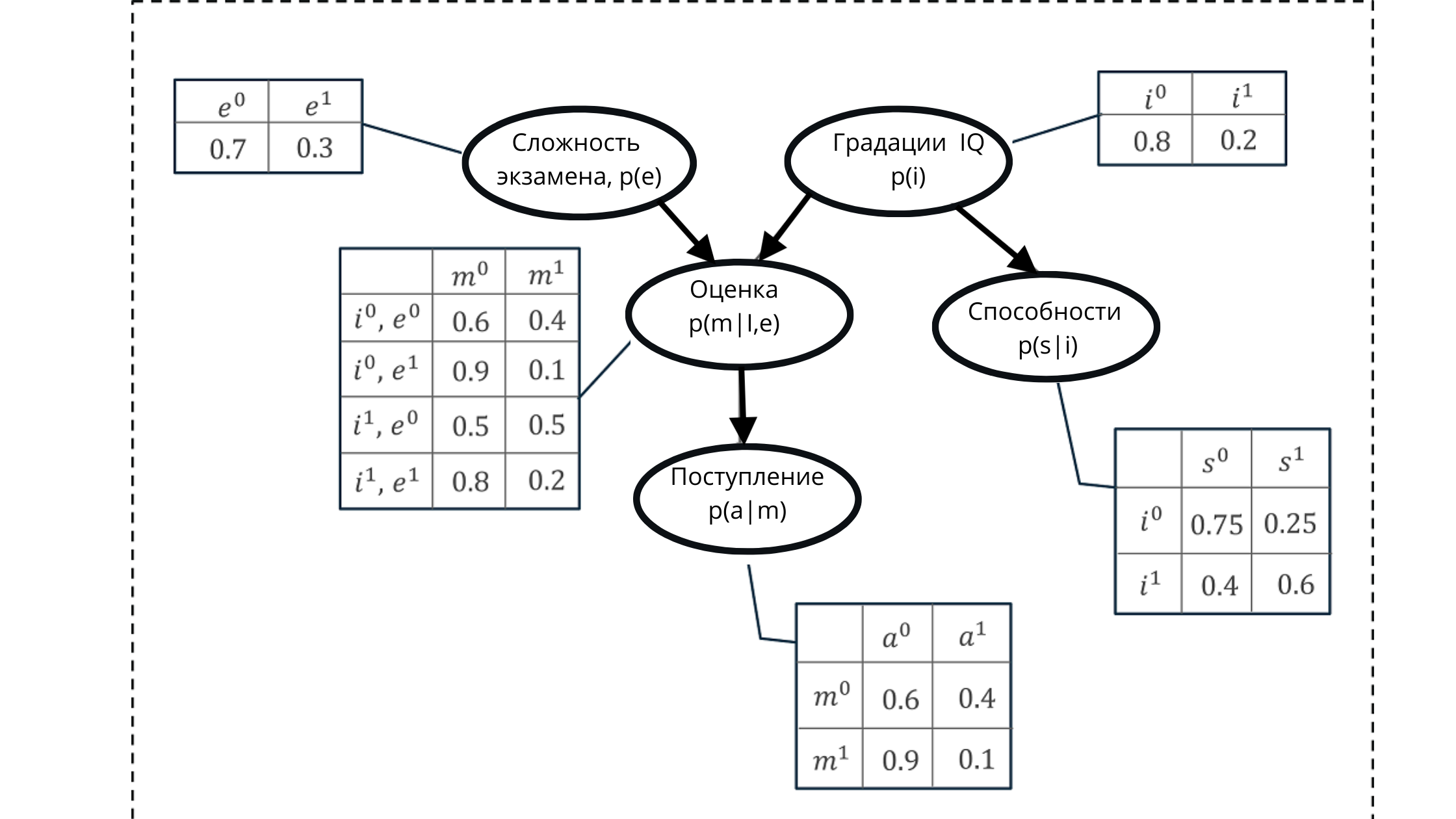
p (a, m, i, e, s) = p (i) * p (e) * p (s | i) * p (a | m) * p (m | i, e) p (a, m, i, e, s) = p (i) * p (e) * p (s | i) * p (a | m) * p (m | i, e)

$p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)p(a, m, i, e, s) = p(i)*p(e)*p(s|i)*p(a|m)*p(m| i,e)$

في الرسم التوضيحي:

p (e) هو التوزيع الاحتمالي لدرجات متغير الاختبار (يؤثر على الدرجة p (m | i، e)))

p (i) هو التوزيع الاحتمالي لدرجات متغير الذكاء (يؤثر على الدرجة p (m | i، e )))

p (m | i، e) - توزيع الاحتمالات لدرجات الصف ، بناءً على مستوى الذكاء وصعوبة الامتحان (يعتمد على p (i) و p (e))

p (s | i) - معاملات الاحتمال لقدرات الطالب ، بناءً على مستوى معدل ذكائه (يعتمد على متغير معدل الذكاء p (i))

p (a | m) هو احتمال قبول الطالب في الجامعة ، بناءً على تقديراته p (m | i، e)

هنا ، أذكر أن خاصية الرسم البياني الحلقي هي انعكاس صلة. في الشكل ، يمكننا أن نرى بوضوح كيف تؤثر العقد الأم على الأطفال وكيف يعتمد الأطفال على الوالدين.

ومن ثم ظهرت صياغة مجموعة القيم المولدة باستخدام شبكات بايزي.

جوهر شبكة بايزي

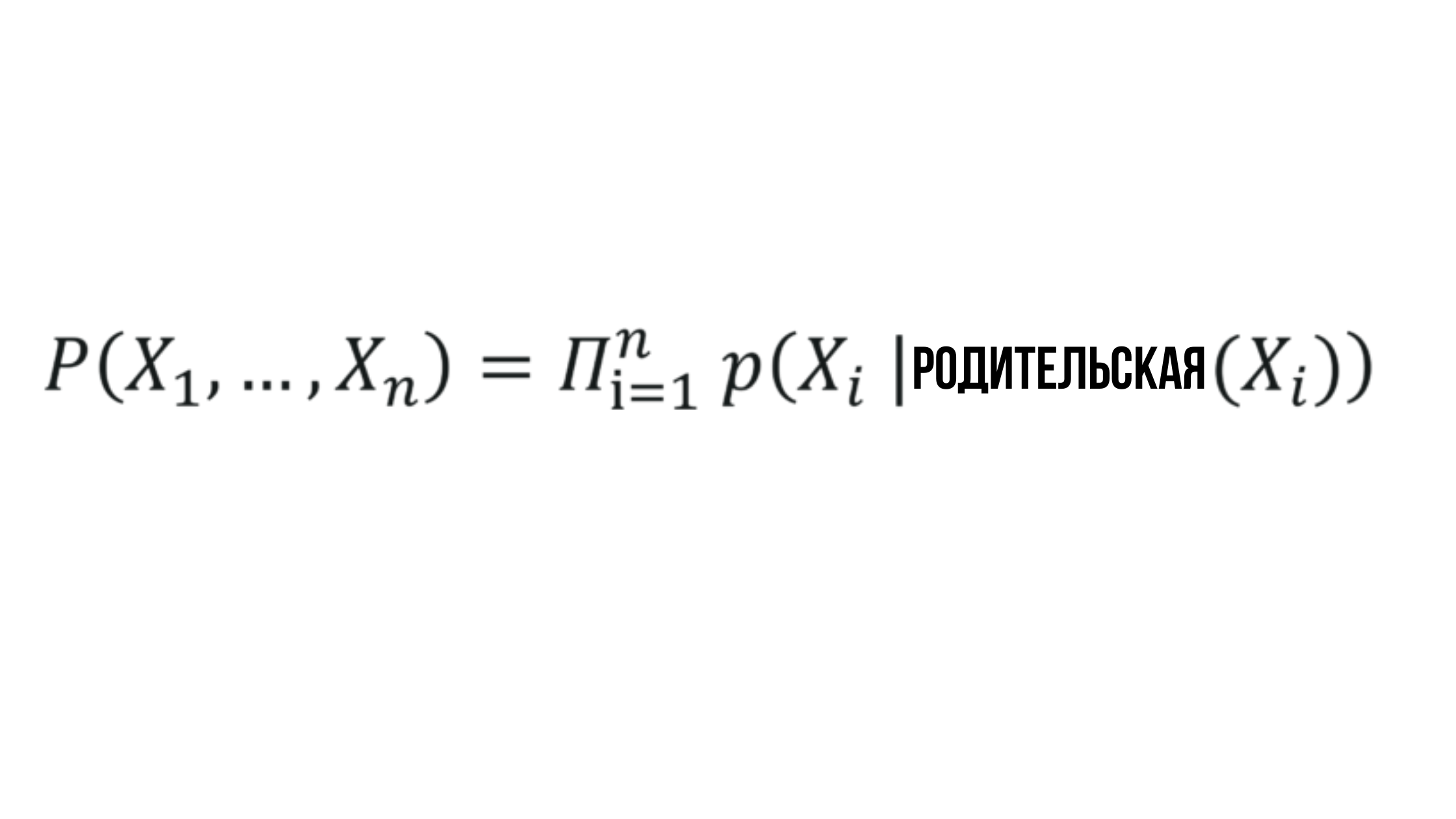
حيث يعتمد الاحتمال X_i على احتمال العقدة الرئيسية المقابلة ويمكن تمثيله بأي قيمة عشوائية.

تبدو بسيطة ، وهي على حق - شبكات بايزي هي واحدة من أبسط الطرق المستخدمة في التحليل الوصفي ، والنمذجة التنبؤية ، وأكثر من ذلك.

شبكة بايزي في بيثون

دعونا نلقي نظرة على تطبيق شبكة بايزي على مشكلة تسمى مفارقة مونتي هول.

خلاصة القول: تخيل أنك مشارك في تنسيق التحديث للعبة "حقل المعجزات". الأسطوانة لم تعد تدور - الآن لا يجب عليك تطبيق F ، ولكن اللعب مع p.

أمامك ثلاثة أبواب ، من المحتمل أن تكون خلفها سيارة واحدة. الأبواب ، التي لا توجد خلفها سيارة ، ستقودك إلى الماعز.

بعد الاختيار ، يفتح زعيم الباقي الذي يؤدي إلى الماعز (على سبيل المثال ، اخترت الباب 1 ، مما يعني أن القائد يفتح إما الباب 2 أو 3) ويدعوك لتغيير اختيارك.

السؤال: ماذا تفعل؟

الحل: في البداية احتمال اختيار باب بسيارة = 33٪ ومعز = 66٪.

إذا بلغت 33٪ ، فإن تغيير الباب يؤدي إلى خسارة => فرصة للفوز == 33٪
إذا بلغت 66٪ ، فإن التغيير يؤدي إلى الفوز => احتمال الفوز == 66٪

من وجهة نظر المنطق الرياضي ، فإن تغيير الباب بشكل إجمالي يؤدي إلى فوز بنسبة 66٪ في المائة وخسارة 33٪. لذلك ، فإن الإستراتيجية الصحيحة هي تغيير الباب.

لكننا نتحدث عن الشبكة هنا ، ويمكن أن يكون هناك الكثير من الأبواب ، لذلك سننقل الحل إلى النموذج.

لنقم ببناء رسم بياني حلقية موجه بثلاث عقد:

باب الجائزة (دائمًا مع سيارة)
باب قابل للتحديد (إما بسيارة أو بماعز)
باب قابل للفتح في الحدث 1 (دائمًا مع عنزة)

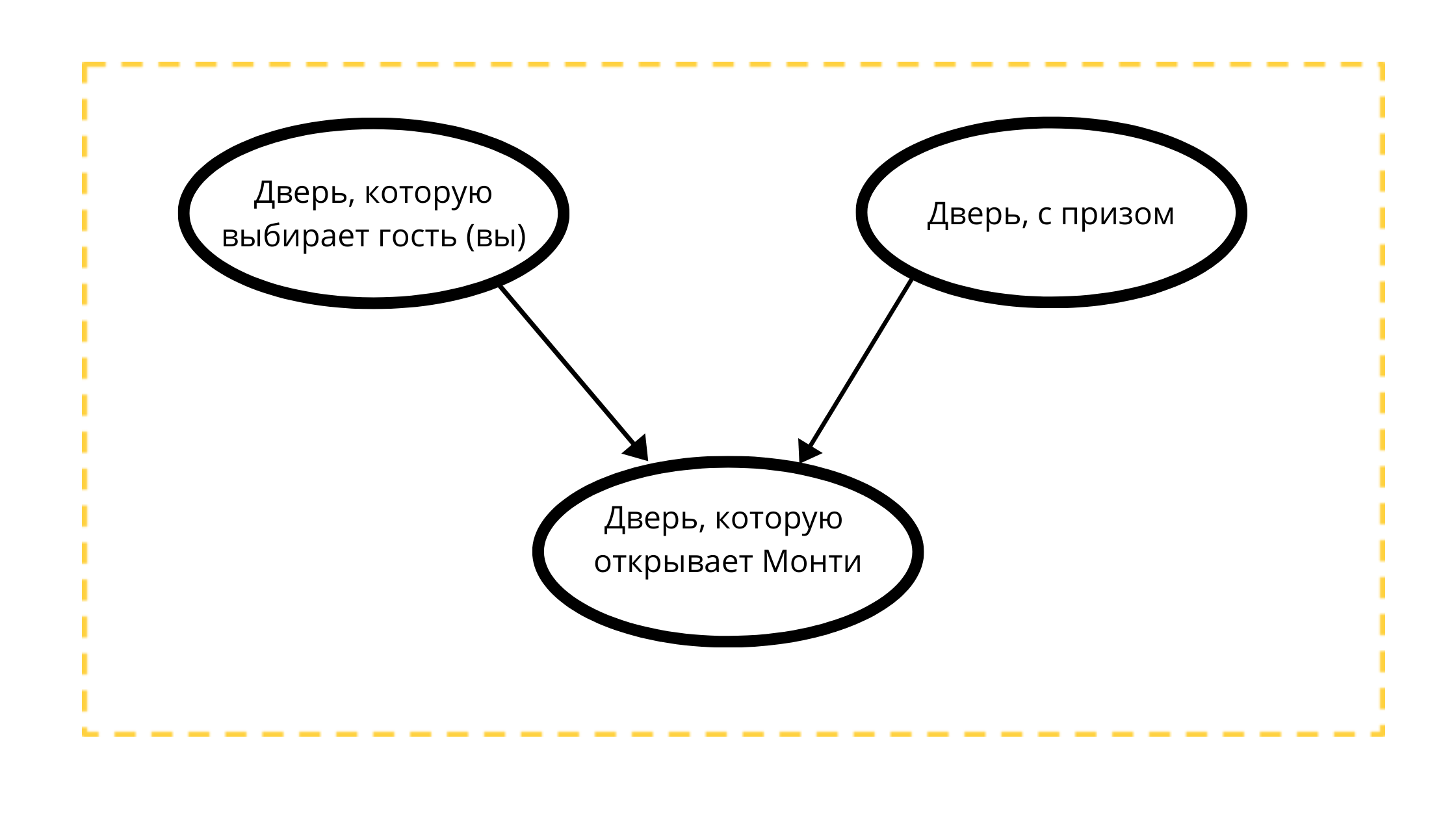
قراءة الكونت:

الباب الذي سيفتحه مونتي يتأثر بشدة بمتغيرين:

الباب الذي اختاره الضيف (أنت) tk Monti 100٪ لن يفتح اختيارك
باب مع جائزة ، ربما يفتح مونتي دائمًا بابًا غير جائزة.

وفقًا للظروف الرياضية للمثال الكلاسيكي ، يمكن تحديد موقع الجائزة على قدم المساواة خلف أي من الأبواب ، تمامًا كما يمكنك على الأرجح اختيار أي باب.

#   
import math
from pomegranate import *
 
#    "  " (   3)
guest =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
#    "   " (    )
prize =DiscreteDistribution( { 'A': 1./3, 'B': 1./3, 'C': 1./3 } )
 
#  ,       ,     
#    
monty =ConditionalProbabilityTable(
[[ 'A', 'A', 'A', 0.0 ],
[ 'A', 'A', 'B', 0.5 ],
[ 'A', 'A', 'C', 0.5 ],
[ 'A', 'B', 'A', 0.0 ],
[ 'A', 'B', 'B', 0.0 ],
[ 'A', 'B', 'C', 1.0 ],
[ 'A', 'C', 'A', 0.0 ],
[ 'A', 'C', 'B', 1.0 ],
[ 'A', 'C', 'C', 0.0 ],
[ 'B', 'A', 'A', 0.0 ],
[ 'B', 'A', 'B', 0.0 ],
[ 'B', 'A', 'C', 1.0 ],
[ 'B', 'B', 'A', 0.5 ],
[ 'B', 'B', 'B', 0.0 ],
[ 'B', 'B', 'C', 0.5 ],
[ 'B', 'C', 'A', 1.0 ],
[ 'B', 'C', 'B', 0.0 ],
[ 'B', 'C', 'C', 0.0 ],
[ 'C', 'A', 'A', 0.0 ],
[ 'C', 'A', 'B', 1.0 ],
[ 'C', 'A', 'C', 0.0 ],
[ 'C', 'B', 'A', 1.0 ],
[ 'C', 'B', 'B', 0.0 ],
[ 'C', 'B', 'C', 0.0 ],
[ 'C', 'C', 'A', 0.5 ],
[ 'C', 'C', 'B', 0.5 ],
[ 'C', 'C', 'C', 0.0 ]], [guest, prize] )
 
d1 = State( guest, name="guest" )
d2 = State( prize, name="prize" )
d3 = State( monty, name="monty" )
 
#  
network = BayesianNetwork( "Solving the Monty Hall Problem With Bayesian Networks" )
network.add_states(d1, d2, d3)
network.add_edge(d1, d3)
network.add_edge(d2, d3)
network.bake()

القيم في المقتطف هي:

أ- الباب الذي يختاره الضيف
ب- باب الجائزة
ج - باب اختاره مونتي

في الجزء ، نحسب قيمة الاحتمال لكل عقد من الرسم البياني. تخضع العقدتان العلويتان في مثالنا لتوزيع احتمالي متساوي ، وتعكس الثالثة التوزيع التابع. لذلك ، من أجل عدم فقدان القيمة ، يتم حساب احتمالات كل من المجموعات المحتملة للعبة لـ .

بعد إعداد البيانات ، أنشأنا شبكة بايزي.

من المهم أن نلاحظ هنا أن أحد خصائص هذه الشبكة هو الكشف عن تأثير المتغيرات المخفية على الملاحظات. في الوقت نفسه ، لا يجب تحديد المتغيرات المخفية أو القابلة للملاحظة أو تحديدها مقدمًا - فالنموذج نفسه يفحص تأثير المتغيرات المخفية وسيفعل ذلك بشكل أكثر دقة كلما زادت المتغيرات التي يتلقاها.

لنبدأ في عمل التنبؤات.

beliefs = network.predict_proba({ 'guest' : 'A' })
beliefs = map(str, beliefs)
print("n".join( "{}t{}".format( state.name, belief ) for state, belief in zip( network.states, beliefs ) ))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333333,
"B" :0.3333333333333333,
"C" :0.3333333333333333
}
],
}
 
monty {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"C" :0.49999999999999983,
"A" :0.0,
"B" :0.49999999999999983
}
],
}

دعونا نحلل الجزء باستخدام مثال المتغير A.

لنفترض أن الضيف اختارها (A).

حدث "هناك جائزة خلف الباب" في مرحلة اختيار باب من قبل ضيف لديه توزيع احتمالي == ⅓ (حيث يمكن أن يكون لكل باب جائزة على حد سواء).

بعد ذلك ، أضف قيمة احتمالات أن يكون الباب هو الجائزة في المرحلة التي يتم فيها اختيار الباب من قبل مونتي. نظرًا لأننا لا نعرف ما إذا كان باب الجائزة قد تم استبعاده من خلال اختيارنا (الضيف) في الخطوة 1 ، فإن احتمال أن يكون الباب جائزة في هذه المرحلة هو 50/50

beliefs = network.predict_proba({'guest' : 'A', 'monty' : 'B'})
print("n".join( "{}t{}".format( state.name, str(belief) ) for state, belief in zip( network.states, beliefs )))
 
guest A
prize {
"class" :"Distribution",
"dtype" :"str",
"name" :"DiscreteDistribution",
"parameters" :[
{
"A" :0.3333333333333334,
"B" :0.0,
"C" :0.6666666666666664
}
],
}
monty B

في هذه الخطوة ، سنقوم بتعديل قيم الإدخال لشبكتنا. الآن يعمل مع التوزيع الاحتمالي الذي تم الحصول عليه في الخطوتين 1 و 2 ، حيث

فرص الفوز على باب اختيارنا لم تتغير (33٪)
تم إلغاء فرص الفوز بالجائزة على الباب الذي فتحه مونتي (ب)
فرص أن تكون جائزة عند الباب ، والتي تركت بدون مراقبة ، أخذت القيمة 66٪

لذلك ، كما تم الاستنتاج أعلاه ، فإن الاستراتيجية الصحيحة من جانب الضيوف لهذه اللعبة هي تغيير الباب - أولئك الذين يغيرون الباب رياضياً لديهم فرص للفوز ضد أولئك الذين لن يغيروا الباب (⅓).

في المثال الذي يحتوي على ثلاث عقد ، تكون الحسابات اليدوية كافية بلا شك ، ولكن مع زيادة عدد المتغيرات والعقد والعوامل المؤثرة ، فإن شبكة بايزي قادرة على حل مشكلة القيمة التنبؤية.

تطبيق شبكات بايزي

1. التشخيص:

التنبؤ بالمرض القائم على الأعراض
نمذجة أعراض المرض الأساسي

2. البحث في الإنترنت:

تشكيل نتائج البحث بناء على تحليل سياق المستخدم (النوايا)

3. تصنيف الوثائق:

مرشحات البريد المزعج على أساس تحليل السياق
توزيع الوثائق حسب الفئة / الفئة

4. الهندسة الوراثية

نمذجة سلوك شبكات تنظيم الجينات على أساس الترابط والعلاقات بين قطاعات الحمض النووي

5. الأدوية:

المراقبة والقيمة التنبؤية للجرعات المقبولة

الأمثلة المذكورة أعلاه هي حقائق. لفهم كامل ، من المناسب أن نتخيل في أي مرحلة يرتبط إنشاء شبكة بايزي وما هي العقد التي يصفها الرسم البياني الذي يصفها.

إن مشكلة مفارقة مونتي هول هي مجرد أساس يسمح للمرء بتوضيح عمل السلاسل على أساس مجموعة من التوزيعات الاحتمالية المستقلة والمستقلة. أتمنى أن أحصل عليه.

ملاحظة: أنا لست آسكا في Python وأتعلم فقط ، لذلك لا يمكنني أن أكون مسؤولا عن كود المؤلف. يسعى نشر هذا المقال عن حبري إلى نشر العمل الفكري للترجمة في العالم. أعتقد في المستقبل أنني سأكون قادرًا على إنشاء دروس خاصة بي - وفيها سأكون بالفعل سعيدًا برؤية أفكار بناءة حول الشفرة.

شبكات بايزي مع بايثون - ماذا ولماذا؟