
ولادة الزحف لا يمكنها الطيران. يمكن استخدام هذه العبارة سواء بالمعنى المجازي أو بالمعنى الحرفي ، لأن المخلوقات التي ليس لها أجنحة (أو أجزاء الجسم المتشابهة في الوظائف) غير قادرة حقًا على التغلب على السماوات. معظمهم على الاقل. لن تكون القاعدة هي القاعدة إذا لم تكن هناك استثناءات. في جانب الرحلة التي لا تحلق ، هناك أيضًا استثناءات - ثعابين شجرة مزخرفة ( Chrysopelea). يمكن لممثلي هذا النوع من الثعبان أن يحلقوا - وهي مهارة مفيدة للغاية بالنظر إلى أنهم يعيشون في تيجان الأشجار المرتفعة فوق الأرض. قرر علماء من جامعة البوليتكنيك في فيرجينيا (الولايات المتحدة الأمريكية) التفكير في هروب ثعبان من حيث علم الحركة. ما هي الميزات التشريحية التي تسمح للأفاعي بالتحليق (السقوط المتحكم به ، ليكون أكثر دقة) ، وما يحدث أثناء الرحلة من وجهة نظر علم الحركة ، وكيف يمكن لهذه الدراسة مساعدة الروبوتات؟ الإجابات على هذه الأسئلة تنتظرنا في تقرير العلماء. اذهب.
أساس البحث
الثعابين المزخرفة هي جنس من ثعابين اعوج موجودة في جنوب وجنوب شرق آسيا. لا يمكن لممثلي هذا الجنس التفاخر بأبعاد كبيرة (طول الجسم فقط من 0.6 إلى 1.5 متر) والسم المميت. على الرغم من أن الفريسة التي يصطادونها في النهار ستختلف مع الأخير. بالنظر إلى الموائل (تيجان الأشجار) ، فإن هذه الثعابين لديها عدد قليل جدًا من الأعداء ، وبالتالي ليس لديهم حاجة خاصة للسم القوي. بالإضافة إلى ذلك ، لديهم تكتيك أكثر فعالية - يعرفون كيف يخططون.

الثعابين الطائرة ، كما يطلق عليها بشكل شائع ، تزحف عبر الأشجار باستخدام قشور قاسية على طول بطنها ، مما يسمح لها بالتحرك عموديا. إذا أراد الثعبان الانتقال من شجرة إلى أخرى ، فإنه يتسلل أولاً إلى حافة الفرع ، ثم يطوي الجسم على شكل الحرف اللاتيني "J" بهدف (لتحديد الزاوية المطلوبة "للإقلاع" وموقع الهبوط). تقول الأفعى ، "دعنا نذهب" ، تدفع جسمها للأمام وللأعلى ، وتسحب في بطنها وتبرز أضلاعها (لذلك يصبح جسمها أكثر استواءً ومقعرًا قليلاً). أثناء الانزلاق ، يقوم الثعبان باستمرار بتحركات جسم السربنتين من جانب إلى آخر ، مما يسمح له بالتحكم في الرحلة والهبوط بهدوء.
منظر جانبي لثعبان طائر مزلق طويل Chrysopelea paradisi.
ميزة إضافية لمثل هذه الطريقة غير المعتادة في الحركة للأفاعي هي توفير مثير للإعجاب للطاقة ، لأن الرحلة أسرع (وأكثر أمانًا) من الزحف ببطء من شجرة إلى أخرى على الأرض. من هذا الوصف الموجز وحده يتضح أن هناك العديد من العناصر المهمة في ميكانيكا طيران الثعبان. زاوية الإقلاع ، شكل الجسم أثناء الإقلاع والطيران ، حركة الجسم أثناء الطيران ، إلخ.
إن أكثر ما يلفت النظر ، وخاصة بالنسبة للمراقبين ، هو جانب حركة الأفعى هو الحركة المتموجة للجسم. يتم استخدام هذه التقنية من قبل العديد من المخلوقات على كوكب الأرض للتحرك على الأرض والمياه. ليس عليك أن تذهب بعيدًا ، لأن الثعابين نفسها تستخدمها بشكل مثالي. يلاحظ العلماء أن الحركة المتموجة على الأرض والمياه قد تم دراستها جيدًا ، لكن مثل هذه الطيور في الهواء لا تزال غامضة.
في الثعابين Chrysopelea ، يتميز التموج بشكل الجسم على شكل S ، وتردد موجي منخفض (1-2 هرتز) ، ومقطع عرضي مسطح من الجسم.
الصورة رقم 1
في الواقع ، تعمل الموجات الهوائية على إعادة ترتيب جسم الثعبان باستمرار ، وتحويله إلى جناح في الشكل ( 1e). أظهرت الأبحاث السابقة أن الطائرات الورقية الطائرة تقوم دائمًا بحركات متموجة أثناء الطيران. ومع ذلك ، لا يزال من غير الواضح ما إذا كان التموج هو الجزء الرئيسي من رحلة ناجحة أم أنه مجرد عادة ، أي الجانب السلوكي للحركة على الأرض ، هاجر إلى الفرار دون أي نوايا.
إذا أخذنا بعين الاعتبار التموج على الأرض والمياه ، فيمكننا أن نفترض أنه يولد قوة دفع في الهواء. على الوسائط الصلبة ، تحدث الحركة المتموجة بسبب قوى التلامس الموزعة على المناطق البطنية والجانبية من الجسم ، وفي الماء ، يتسبب إزاحة أو امتصاص السوائل على طول الجسم في الحركة إلى الأمام. في كلتا الحالتين ، تعمل القوة الدافعة النقية في المقام الأول في مستوى التموج. يمكن استخدام تعديل الجسم خارج المستوي (العمودي) لأغراض ثانوية مثل تقليل المقاومة أو زيادة القوة الطبيعية.
ولكن بالنسبة للطائرات الورقية الطائرة ، يتطلب التخطيط الناجح توليد قوى ديناميكية هوائية ضرورية لتعويض وزن الحيوان. يتم إنشاء قوى الرفع والمقاومة من خلال تدفق الهواء عبر الجسم المسطح عندما يتم تسريعه إلى أسفل بسبب الجاذبية ، ومن المحتمل ألا تؤدي الحركة التبادلية التي تسببها تقلصات العضلات إلى زيادة توليد القوة.
منظر أمامي للإقلاع وتسطيح الأفعى الطائرة Chrysopelea paradisi.
يجب أن تعمل القوى الديناميكية الهوائية الناتجة خارج مستوى الموجة ، ويجب على الموجة نفسها أن تغير باستمرار توزيع القوى على جسم الثعبان. تجدر الإشارة أيضًا إلى أن الطائرات الورقية الطائرة يمكن أن "ترفرف" ليس فقط أفقيًا ، بل عموديًا. وهذا يعني أنه في نموذج الطيران الثعبان هناك على حد سواء في الملعب عناصر * و لفة العناصر * .
الملعب * - الحركة الزاوية بالنسبة للمحور الأفقي المستعرض للقصور الذاتي.في هذه الدراسة ، قرر العلماء إلقاء نظرة فاحصة على دور التموج في تحليق طائرة ورقية. باستخدام لقطات عالية السرعة لرحلة الثعبان ، تمكن العلماء من تحديد كمية الموجة في الهواء. جعلت البيانات التي تم الحصول عليها من الممكن إنشاء نموذج دقيق ثلاثي الأبعاد لرحلة الطائرات الورقية.
لفة * - حركة زاوية حول محوره الطولي.
نتائج البحث
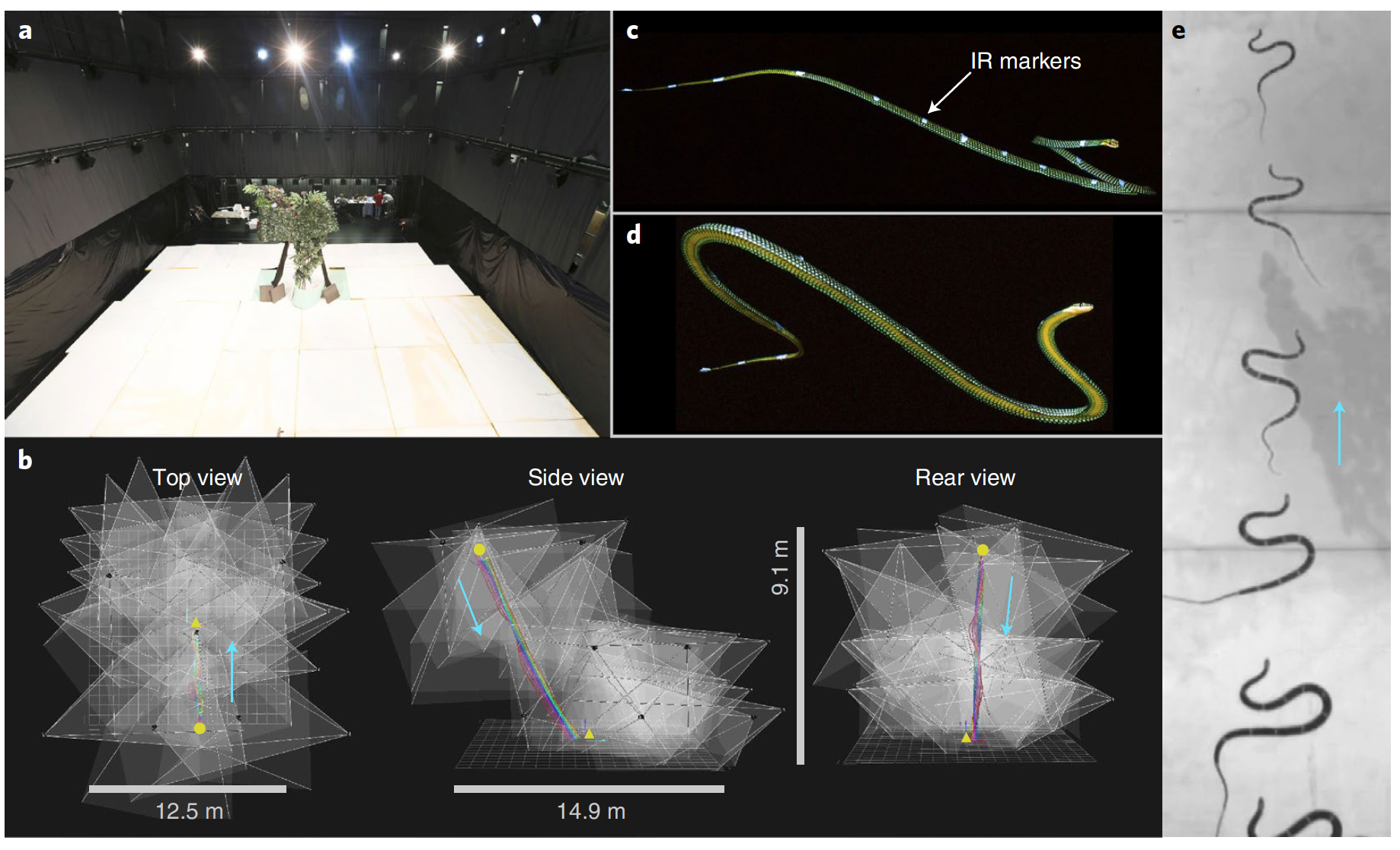
يتكون تموج الهواء من حزمة من موجات الانحناء الأفقي والرأسي. تم وضع علامات 17-17 على طول جسم الثعابين (7 أفراد) المشاركين في إطلاق النار على الطائرة (منطقة الإقلاع العالية من 8.3 م). يسمح لك تقييم التغيير في موضع هذه العلامات بتحديد بنية التموج بدقة أثناء الرحلة.
المنظر العلوي لاختبار انزلاق الأفعى الطائرة Chrysopelea paradisi.
تم الحصول على علامات الأشعة تحت الحمراء أثناء انزلاق ثعبان طائر ، Chrysopelea paradisi.
بعد 36 ملاحظة عملية ، ابتكر العلماء نموذجًا ثلاثي الأبعاد لجسم الثعبان ( ص ).
تطوير نموذج ثلاثي الأبعاد للطائرة الورقية الطائرة Chrysopelea paradisi وفقًا لبيانات التقاط الحركة.
باستخدام المتجه المماس (t̂ = ∂r / ∂s) ، كان من الممكن تحليل الموجة إلى موجتين منحنيتين زاويتين تتحرك على طول الجسم.
يتم إعطاء الموجات الأفقية والرأسية بالصيغ التالية:
θ̅ (s، t) = -tan -1 t̂ x / t̂ y
و
ψ̅ (s، t) = sin -1 t̂ z
حيث θ̅ (s، t) و ψ̅ (s، t ) هي الزوايا المحلية التي يشكلها الجسم بالنسبة للاتجاهين الأفقي والرأسي ، كدالة لطول القوس s والوقت t.
تشير البيانات إلى أن الطائرات الورقية الطائرة تستخدم موجتين: موجة أفقية بسعة كبيرة وموجة رأسية بسعة أقل ، وكلاهما ينتقلان بالتتابع إلى أسفل الجسم من الرأس إلى الذيل (الصورة رقم 2).

الصورة رقم 2
تتشكل هذه الموجات بعد العبور الأولي ، عندما تقفز الأفعى في وضع مستقيم نسبيًا ثم تشكل وضعًا مميزًا على شكل حرف S للتخطيط.
هناك أربع ميزات لتمايل الهواء تربط الموجة العمودية مع الموجة الأفقية ( 2 أ ). أولاً ، تحتوي الموجة العمودية على ترددات مكانية وزمنية ضعف تردد الموجة الأفقية. هذا يشير إلى أن الجسم لديه ضعف عدد الانحناءات الرأسية مثل الانحناءات الجانبية ( 2 أ ،2 هـ ). ثانيًا ، يمكن تحديد الانحناءات U على جسم طائرة ورقية تحلق على أنها التقاطع الصفري في الرسم البياني لزاوية الانحناء ( 2 ب ). ثالثًا ، هذه التقاطعات هي ارتفاعات الأمواج الرأسية ، مما يشير إلى أن الموجات الأفقية والرأسية خارج الطور 90 درجة. رابعًا ، يحدث الحد الأقصى للانحناء خارج المستوى عند الانحناءات U وحوالي منتصف الأجزاء المستقيمة. في U-bends ، يتم طي المقطع العرضي "لجناح" الثعبان بسبب حركة الجسم خارج الطائرة ( 1c ، 1d ).
يتغير شكل موجات السفر بمرور الوقت مع تسارع الطائرة الورقية وإنتاج قوى ديناميكية هوائية ، ولكن بعض الميزات لا تزال شائعة. الموجة الأفقية هي جيبية مسطحة السطح ، يعتمد اتساعها (80-120 درجة) على عدد الفترات المكانية ، مع فترات أقل تؤدي إلى زوايا انحناء أفقية أعلى. الموجة العمودية هي جيبية ضيقة الذروة مع أحواض واسعة بسعات تتراوح من 20 درجة إلى 45 درجة.
أظهر التقييم الكمي للخصائص المكانية والزمنية للموجات أن الثعابين تستخدم موجات أفقية تتراوح من 1 إلى 1.5 فترات مكانية وتردد موجي من 1 إلى 1.7 هرتز وموجات رأسية مع 2-3 فترات مكانية وتردد موجي من 2-3 إلى هرتز.
هناك عنصر إضافي في تموج الهواء ، والذي أطلق عليه العلماء "انحناء الظهراني" ، يمثل الحركة العلوية والسفلية للجزء الخلفي من الجسم بالنسبة للرأس. كانت زاوية الميل لهذا الانحناء من -20 درجة إلى 30 درجة. كان الانحناء الظهري المركزي موجودًا دائمًا في الرحلات الجوية المرصودة ، ولكن لم يكن له علاقة كبيرة بعدد الفترات المكانية.
لتحديد درجة تأثير العلاقة بين الموجات الأفقية والرأسية بدقة ، وكذلك تأثير الانحناء الظهري المركزي على ديناميكيات الطيران ، ابتكر العلماء نموذجًا دقيقًا تشريحيا لثعبان أثناء الطيران. تسمح السيطرة على النموذج ، وفقًا للعلماء ، بالتحقق المنهجي من كيفية تأثير مكونات الموجة (اتساع الموجة الأفقية ، وعدد الفترات المكانية وتواتر الموجة) على ديناميكيات التخطيط على المدى القصير والطويل.
تم تصميم الموجة الأفقية على أنها جيبية ذات ذروة مسطحة ذات سعة كبيرة ، والموجة الرأسية مصممة على أنها جيبية ذات سعة صغيرة:
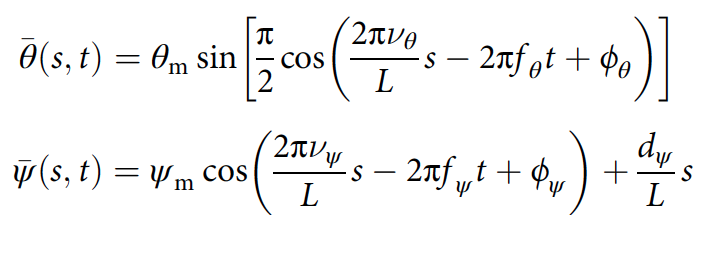
حيث θ m و ψ m هما الحد الأقصى لزاوية الانحناء الأفقي والرأسي ؛ ν هو عدد الفترات المكانية ؛ و - تردد الموجة ؛ ϕ - التحول الطوري ؛ d ψ - زاوية الانحناء الظهري المركزي ؛ L - طول الجسم ( 2f ، 2g ).
ترتبط الموجات الأفقية والعمودية في البيانات الحركية ( 2 ): ν ψ = 2ν θ ، f ψ = 2f θ و ϕ ψ = 2 (ϕ θ- π / 2). هذا يبسط النموذج بشكل كبير إلى 5 متغيرات تحدد شكل الجسم: θ m و ψ m و ν θ و f θ و d ψ .
يتم حساب الموضع r = [x، y، z] للجسم بالنسبة لمركز الكتلة على النحو التالي: ∂ s x = cosψ̅sinθ̅، y s y = -cosψ̅cosθ̅ و z s z = sinψ̅.
يتم تحديد موضع مركز الكتلة R 0 واتجاه الجسم (زوايا الانحراف * ، والانحدار واللف) من خلال دمج معادلات الحركة الانتقالية والدورانية.
ياو * - حركات زاوية حول المحور الرأسي.
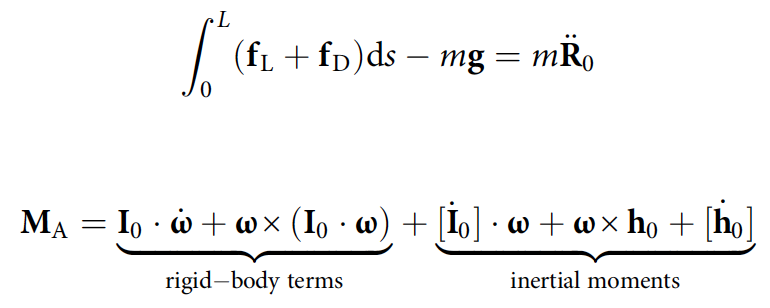
حيث f L و f D هما قوى الرفع والمقاومة اللامحدودة ؛ M A هي اللحظة الهوائية ؛ م هي كتلة الأفعى.
للتأكد من أن النموذج الرياضي يعطي نتائج واقعية جسديًا ، قام العلماء بنمذجة الرحلات الجوية باستخدام المعلمات التي تم الحصول عليها أثناء الملاحظات الفعلية لتخطيط الثعابين الحقيقية (يتم عرض مقارنة للنماذج والملاحظات في الصورة أدناه).

الصورة رقم 3 على
سبيل المقارنة ، يعمل النموذج ، ولكن لديه بعض عدم الدقة الطفيفة التي تحتاج إلى تصحيح في المستقبل.
للتحقق من تأثير التموج على خصائص التخطيط ، تم إجراء عمليتي محاكاة: مع f θ = 0 Hz (بدون تموجات) و f θ= 1.2 هرتز (متوسط تكرار الموجات في الثعابين). في كلتا الحالتين ، اختلفت ν θ و θ m ( 4a ).

الصورة №4
جعلت البيانات الحركية لشكل جسم الثعبان في النموذج من الممكن الحصول على 121 شكلًا مع 1 ≤ ν θ ≤ 1.5 من موجات الجسم واتساع الموجة الأفقية في النطاق 90 درجة ≤ θ م ≤ 119 درجة. علاوة على ذلك ، تم استخراج أشكال الجسم المرصودة (الجزء الأوسط من الرسم البياني ، مفصولة قطريًا ؛ 4 ب ) من هذا الصفيف . يحتوي جزء الرسم البياني الموضح أدناه على أشكال الجسم "المفتوحة" (التي تشبه الحرف S) ، والجزء العلوي - "مغلق" (يشبه علامة اللانهاية).
تم الحفاظ على اتساع الموجة العمودية والزاوية الظهرانية المركزية عند مستوى ثابت: 20 درجة و 10 درجة على التوالي. اعتبرت المحاكاة كاملة عندما لامس مركز كتلة جسم الثعبان الأرض (الهبوط) أو عندما تجاوزت أي من زوايا الاتجاه قيمة العتبة 85 درجة. إذا حدث ذلك ، فقد اعتبر التخطيط غير مستقر ، أي ليس مثل الطبيعة. أثناء المحاكاة ، تم اختبار كل من الديناميكيات قصيرة المدى (بدء الارتفاع 10 م) والديناميكيات طويلة المدى (ارتفاع البدء 75 م) مع / بدون تموج.
يوضح النموذج أن تموج الهواء له تأثير إيجابي على خصائص التخطيط ، وعادة ما يزيد المسافات الأفقية والرأسية التي تم قطعها قبل أن يصبح الثعبان المحاكي غير مستقر.
محاكاة ثعبان طائر ينزلق مع وتموج بدون تموج.
أظهرت الانزلاقات القصيرة بارتفاع إطلاق 10 أمتار معامل استقرار جيد في وجود تموجات (94٪). إذا لم يتم تضمين التموج في النموذج ، فإن 50 ٪ فقط من الرحلات الجوية كانت مستقرة. يزيد التموج أيضًا من مسافة التخطيط (من 4 م إلى 4.3 م).
عند تخطيط التخطيط من ارتفاع 75 م ، زاد التموج من المسافة الأفقية والرأسية قبل أن يتجلى عدم الاستقرار في 86 ٪ من عمليات الإطلاق. في هذه الحالة ، زاد التموج أيضًا من مسافة الرحلة في 92 ٪ من عمليات الإطلاق. كما زاد التموج متوسط المسافة الأفقية بمقدار 6.9 م.
لمعرفة تأثير اتساع الموجة العمودية والانحناء الظهري المركزي على الديناميات المنزلقة ، تم استخدام قيم مختلفة لهذه المعلمات في النمذجة وتم النظر في النتائج.
الصورة رقم 5
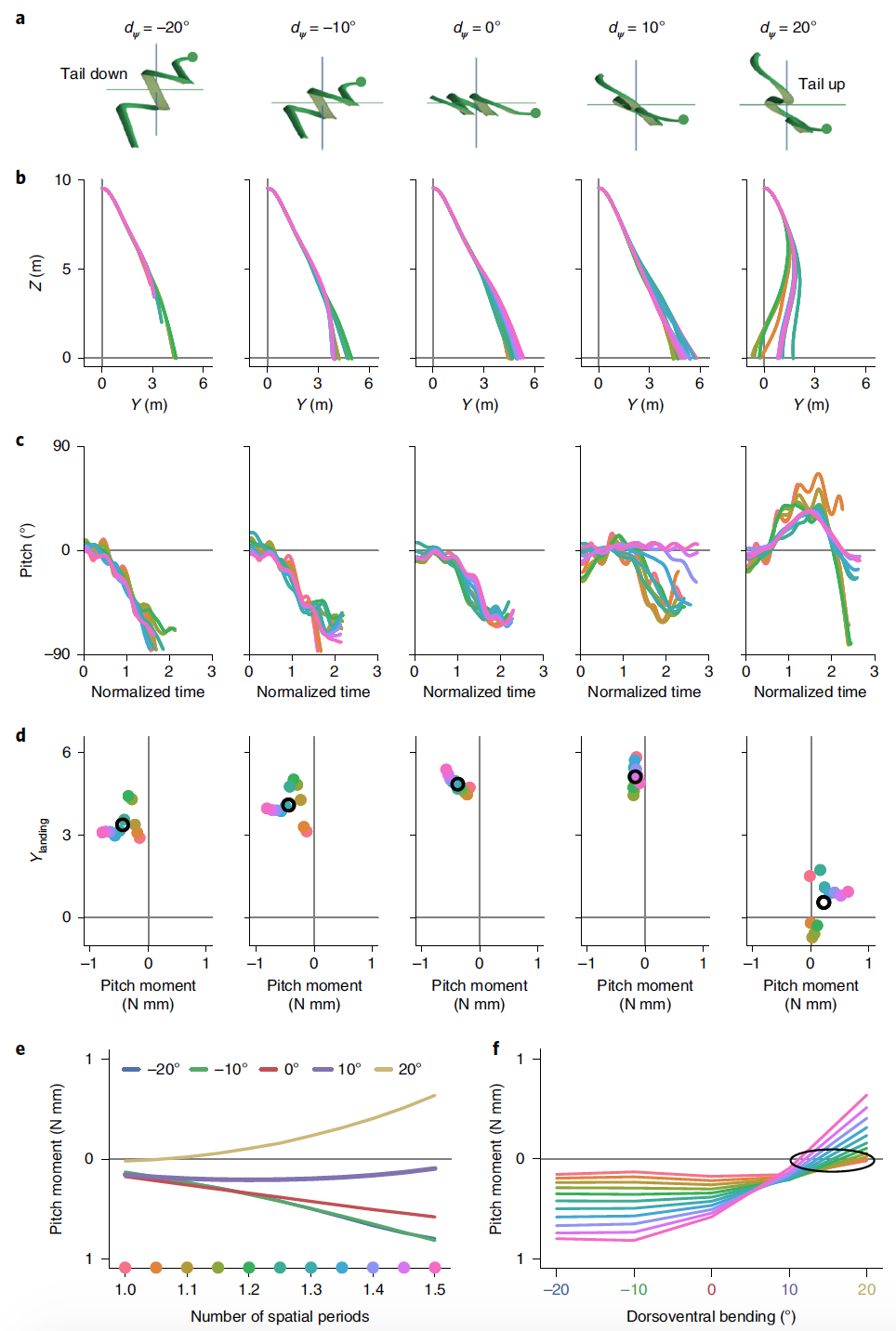
تمت محاكاة التخطيط باستخدام ψ m = 0 ° و 10 ° و 20 ° والانحناء الظهري المركزي من -20 ° إلى 20 ° في خطوات 10 درجات ( 5 أ ) لـ 11 شكل مختلف من الجسم.
التذبذب العمودي له تأثير ضئيل نسبيًا على مسار الانزلاق ، في حين أن الانحناء الظهري المركزي له تأثير كبير.
ثعبان مسطح تماما (. م= 0 °) ، الذي لم يلاحظ أبدًا أثناء الاختبارات التجريبية ، أظهر أسوأ النتائج المتوقعة. أدت زيادة اتساع الموجة العمودية إلى زيادة كفاءة التخطيط بسبب التواء المقطع العرضي في الطائرة ، مما يوفر زاوية أكثر ملاءمة لإنشاء القوة ( 2j ).
على النقيض من اتساع الموجة العمودية ، كان للانحناء الظهري المركزي تأثيرًا ملحوظًا على خصائص الانزلاق ، خاصة على الملعب.
في ψ م = -20 درجة مع الجزء الخلفي من الجسم تحت الرأس، وكان التخطيط لا الضحلة، بدلا من ذلك، أصبح غير مستقر في ارتفاع قبل أن تنخفض بنسبة 10 م في ψ. م= 20 درجة مع الجزء الخلفي من الجسم فوق الرأس ، يكون المسار منحنيًا للخلف ، مع هبوط بعض أشكال الجسم خلف القفزة. هذا التخطيط الضعيف يبرره الميل لأعلى في الجسم. ومع ذلك ، كان للطائرات الشراعية مع المعلمات المذكورة أعلاه استقرار دوران جيد.
تم إجراء المحاكاة غير الدورية لاختبار العلاقة بين ثني الجسم الظهري المركزي ، والأداء ، والانزلاق. بدلاً من حل النظام غير الخطي المقترن بالمعادلتين رقم 4 ورقم 5 ، أخذ العلماء عينات من القوى الديناميكية الهوائية في مراحل مختلفة من الجسم خلال دورة التموج. بعد ذلك ، تم دمج المعادلة رقم 4 هنا ، وتم حساب موضع وسرعة مركز الكتلة.
في الواقع ، هذا التلاعب هو تجربة "نفق رياح افتراضي" ، حيث يتم استخدام النموذج الديناميكي لحساب القوى الموزعة التي تعمل على الجسم أثناء تسارعه. تزيل هذه الطريقة العلاقة بين الحركة الانتقالية والحركة الدورانية من أجل تحديد المساهمات الأيرودينامية الفردية والقصور الذاتي في الحركة الدورانية.
مع زيادة الانحناء الظهري المركزي من -20 درجة إلى 10 درجة ، يزداد موضع جلوس الثعبان المحاكي مع زيادة درجة الملعب نحو الصفر ( 5 د ). عند الانحناء الظهري 20 درجة ، تصبح لحظة الرمي بمتوسط الطور إيجابية وينخفض أداء الانزلاق.
لكل زاوية انحناء دورانية مركزية ، تعتمد كفاءة التخطيط ومتوسط العزم المائل أيضًا على الشكل المستخدم ، ولا سيما على عدد الفترات المكانية واتساع الموجة الأفقية. بالنسبة لأي شكل جسم في لحظة التخطيط ، فإن الانحناء الظهري المركزي له تأثير كبير على متوسط لحظة الرمية ، ومع زيادة عدد الفترات المكانية ، تتباعد اللحظات ، وتصبح أكثر إيجابية أو سلبية اعتمادًا على d ψ . تتوافق
علامات لحظات الملعب التي تبلغ متوسط الطور عند 5e مع المنحدر الصاعد أو المنحدر الموضح عند 5c وأداء الانزلاق الناتج عند 5b . في 5 ويظهر أنه بالنسبة لأشكال الجسم ذات أصغر فترة مكانية ، فإن متوسط لحظة الرمية ستكون الأصغر.
من البيانات الموصوفة أعلاه ، يمكن افتراض أن الموجة العمودية تتسبب في خروج الجسم من المستوى ، وتغيير الاتجاه المحلي لـ "الجناح المسطح" (شكل جسم الثعبان أثناء الانزلاق) بمساعدة تدفق الهواء. يتحكم الانثناء Dorsoventral في حجم وعلامة اللحظة الرئيسية الديناميكية الهوائية التي تعمل على الجسم. يمكن للطائرة الورقية السيطرة على لحظة الرمي عن طريق تغيير زاوية الانحناء الظهري أو الشكل الموجي الأفقي أثناء الطيران.
ونتيجة لذلك ، يلعب انحناء الجسم الظهري المركزي دورًا مهمًا للغاية في استقرار الانزلاق والهبوط الناجح والقدرة على تغيير مسار الانزلاق أثناء تنفيذه.

الصورة رقم 6
يسمح لك تحليل المرحلة عن طريق حساب المتوسط بالمساهمة النسبية للحظات الديناميكية الهوائية والقصور الذاتي في ديناميكيات التخطيط.
المعادلات رقم 5 تعني أن اتجاه الجسم يتأثر بكل من القوى الديناميكية الهوائية والتوزيع الجماعي المتغير. تزداد المساهمة الديناميكية الهوائية ( 6 أ ) مع الوقت مع زيادة السرعة ، بينما تظل المساهمة القصور الذاتي ( 6 ب ) ثابتة. كلتا المرات دورية ، وحظة العرض فقط تظهر متوسط طور غير صفري.
في البداية ، تسود لحظات القصور الذاتي بالقرب من محاور الملعب واللف ، ولكن خلال دورة تشبه الموجة تتناقص مساهمتها بسرعة. لحظات الانحراف بالقصور الذاتي ، كقاعدة عامة ، هي مرتبة من حيث الحجم أكبر من لحظات الانقسام الديناميكي الهوائي وأكثر من لحظات القصور الذاتي حول محاور أخرى. تحدث لحظات الانحراف الذاتي بسبب موجة أفقية ذات سعة كبيرة وجسم عريض على شكل S. تشير هذه النتيجة إلى أن الطائرات الورقية الطائرة يمكن أن تستخدم دوران القصور الذاتي كآلية للمناورة.
لمعرفة أكثر تفصيلا مع الفروق الدقيقة في الدراسة، أوصي بأن تنظر في تقرير العلماء و مواد إضافية لذلك.
ويمكن لأولئك الذين يرغبون في التعرف على البرنامج المستخدم لتحليل التخطيط للطائرة الورقية الطائرة اتباع هذا الرابط .
الخاتمة
في هذه الدراسة ، استخدم الباحثون أحدث تقنيات التقاط الحركة والنمذجة ثلاثية الأبعاد لإنشاء نموذج دقيق تشريحيا لثعبان طائر.
كان من الصعب أيضًا في يوم من الأيام فهم ديناميكيات رحلة الطيور ، لكنها لم تربك العلماء مثلما تفعل الأفعى الطائرة. في الطبيعة ، لا توجد أمثلة كثيرة على الرحلات الجوية بدون أجنحة ، وكلها مرتبطة باستخدام آليات غير قياسية تسمح للحيوان بالتخطيط ، ولا تقع على الأرض بالحجر.
في حالة الثعابين الطائرة ، يلعب التموج الذي يتم ملاحظته في حركة الثعابين الزاحفة والعائمة دورًا مهمًا للغاية. آلية إضافية لتحقيق الاستقرار في التخطيط هي تصحيح الزاوية الظهريّة المركزيّة لثني الجسم. من خلال الجمع بين هذه العناصر معًا ، يمكن للطائرات الورقية الطائرة الطيران من شجرة إلى أخرى ، مع معرفة مكان الزراعة في المستقبل.
يعتقد مؤلفو هذا العمل أن بياناتهم لم تسمح لنا فقط بفهم أفضل لعادات ثعابين الأشجار المزينة ، ولكن أيضًا للحصول على إلهام إضافي لإنشاء روبوتات تشبه الثعابين. نعم ، هذه الروبوتات موجودة بالفعل. يزحفون ، ويمكنهم التحرك فوق الأسطح الصعبة واختراق الأماكن التي يصعب الوصول إليها ، ولكن هل يمكنهم الطيران؟
مع هذا المنطق ، سيشبه عالمنا قريبًا مدينة الآلات من "ماتريكس" ، حيث زحف مخلوقات روبوتية غير عادية للغاية (ومخيفة قليلاً) على طول الجدران ، وكان من الصعب فهم الغرض منها. لا يمكن خداع رغبة الشخص في صنع نسخة روبوتية من كل شيء يحيط به. هذه هي طبيعتنا - لفهم كل شيء ، لمعرفة كل شيء ، لتكون قادرة على خلق ما فعلته الطبيعة بشكل جميل أمامنا. إذا كانت هناك فائدة أكبر بكثير من الأذى من الأفاعي الآلية والعناكب والكلاب وغيرها من الحيوانات الروبوتية ، فإن هذه الدراسات لها ما يبررها تمامًا.
شكرًا على المشاهدة ، ابقوا فضوليين واستمتعوا بعطلة نهاية أسبوع رائعة يا رفاق!
الجمعة خارج القمة:
, .
, .
خارج 2.0:
, :)
, :)
القليل من الدعاية
أشكركم على البقاء معنا. هل تحب مقالاتنا؟ هل تريد مشاهدة محتوى أكثر إثارة للاهتمام؟ ادعمنا عن طريق تقديم طلب أو التوصية للأصدقاء ، VPS السحابي للمطورين من 4.99 دولارًا ، وهو نظير فريد لخوادم مستوى الدخول التي اخترعناها لك: الحقيقة الكاملة حول VPS (KVM) E5-2697 v3 (6 نوى) 10 جيجابايت DDR4 480 جيجابايت SSD 1 جيجابت في الثانية من $ 19 أو كيفية تقسيم الخادم بشكل صحيح؟ (تتوفر الخيارات مع RAID1 و RAID10 ، حتى 24 مركزًا وذاكرة DDR4 تصل إلى 40 جيجابايت).
Dell R730xd أرخص مرتين في مركز بيانات Equinix Tier IV في أمستردام؟ فقط لدينا 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV من 199 دولارًا في هولندا!Dell R420 - 2x E5-2430 بسرعة 2.2 جيجاهرتز 6C وسعة 128 جيجابايت DDR3 2x960 جيجابايت SSD 1 جيجابت في الثانية 100 تيرابايت - بدءًا من 99 دولارًا! اقرأ عن كيفية بناء مبنى البنية التحتية الطبقة باستخدام خوادم Dell R730xd E5-2650 v4 بتكلفة 9000 يورو مقابل بنس واحد؟