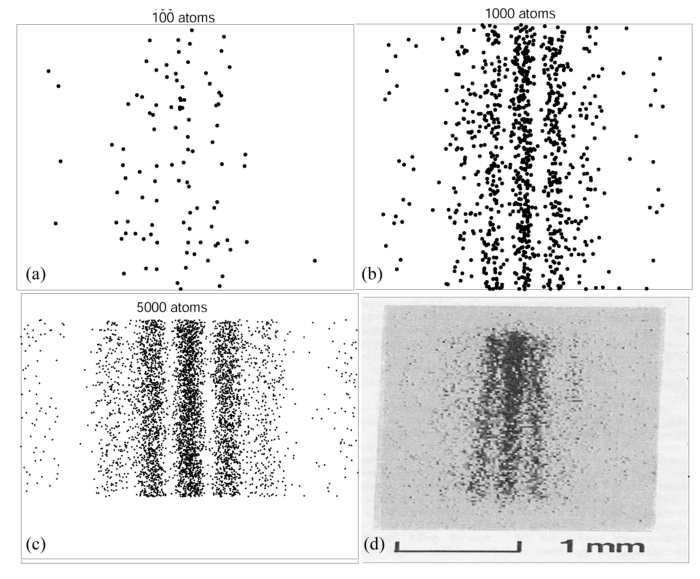
في ملحق المقال ، يوفر مسار الجسيم مواد قطع: تكامل المسار ، وتجربة ثنائية الفجوة على ذرات النيون الباردة ، وإطارات الانتقال الجسيمي ، ومشاهد أخرى من القسوة والطبيعة الجنسية.
في رأيي ، لا يمكن أن تكون هناك طريقة أخرى لاعتبار الشكلية الرياضية متسقة منطقيًا من إثبات أن عواقبها تنحرف عن التجربة ، أو لإثبات أن تنبؤاتها لا تستنفد إمكانيات الملاحظة.
نيلز بور
في الختام ، يود المؤلف أن يذكر أننا ندرك سببين جيدين فقط لرفض نظرية تفسر مجموعة واسعة من الظواهر. أولاً ، النظرية ليست متسقة داخليًا ، وثانيًا ، ليست متسقة مع التجارب.
ديفيد بوم
في وقت سابق ، تعلمنا من أين تأتي معادلة شرودنغر ، ولماذا يتم أخذها من هناك ، وكيف يتم أخذها بطرق مختلفة.
الآن ، نقسمها إلى معادلتين حقيقيتين. للقيام بذلك ، تخيل psi في شكل قطبي, :
, . , S -, - - :
, -, , , , S, , , , . , , . -.
— , . , , , . , , , .
, , , . . . , , , .
, , , . , ( - ). :
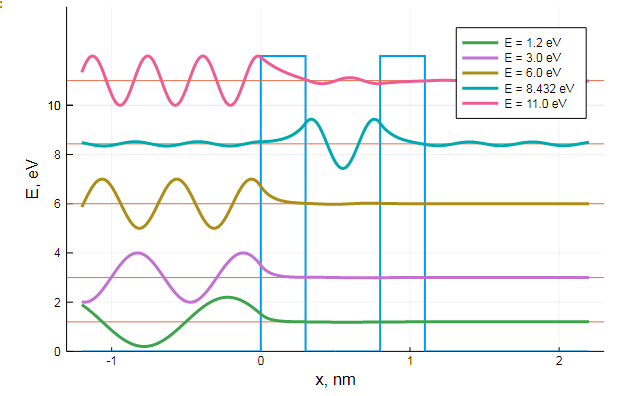
()
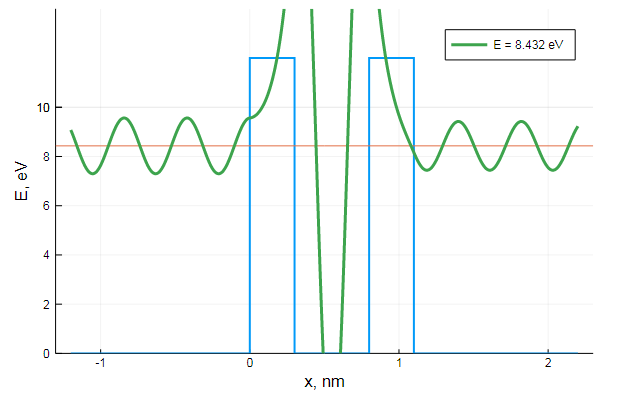
, , , : ,
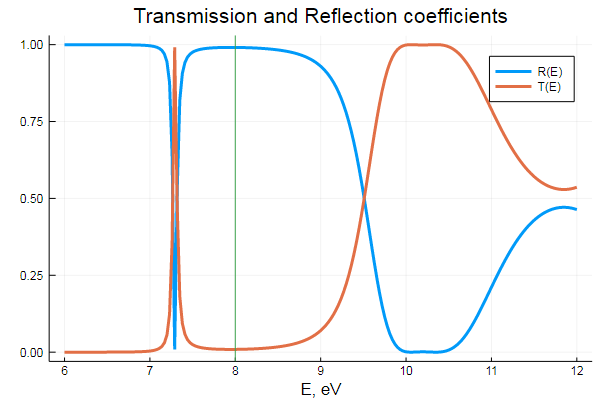
-, :
using LinearAlgebra, SparseArrays, Plots
const ħ = 1.0546e-34 # J*s
const m = 9.1094e-31 # kg
const q = 1.6022e-19 # Kl
const nm = 1e-9 # m
const fs = 1e-12; # s
function wavefun()
gauss(x) = exp( -(x-x0)^2 / (2*σ^2) + im*x*k )
k = m*v/ħ
#
Vm = spdiagm(0 => V )
H = spdiagm(-1 => ones(Nx-1), 0 => -2ones(Nx), 1 => ones(Nx-1) )
H *= ħ^2 / ( 2m*dx^2 )
H += Vm
A = I + 0.5im*dt/ħ * H #
B = I - 0.5im*dt/ħ * H #
psi = zeros(Complex, Nx, Nt)
psi[:,1] = gauss.(x)
for t = 1:Nt-1
b = B * psi[:,t]
# A*psi = b
psi[:,t+1] = A \ b
end
return psi
enddx = 0.05nm # x step
dt = 0.01fs # t step
xlast = 400nm
Nt = 260 # Number of time steps
t = range(0, length = Nt, step = dt)
x = [0:dx:xlast;]
Nx = length(x) # Number of spatial steps
a1 = 200nm
a2 = 200.5nm # 5
a3 = 205nm
a4 = 205.5nm
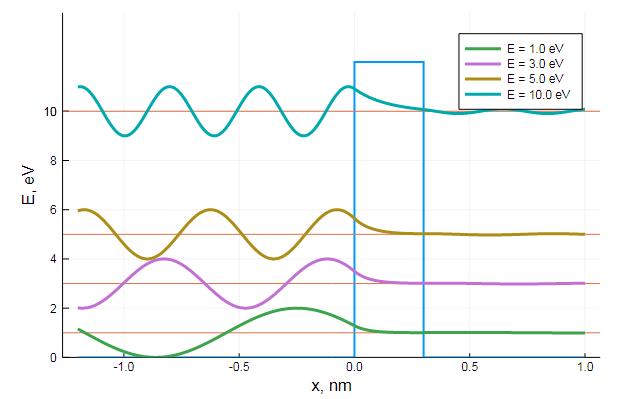
#V = [ a1<xi<a2 ? 2q : 0.0 for xi in x ] # 2 eV
V = [ a1<xi<a2 || a3<xi<a4 ? 2q : 0.0 for xi in x ] # 2 eV
x0 = 80nm # Initial position
σ = 20nm # gauss width
v = -120nm/fs;
@time Psi = wavefun()
P = abs2.(Psi);
function ψ(xi, j)
k = findfirst(el-> abs(el-xi)<dx, x)
k == nothing && ( k = 1 )
Psi[k, j]
end
function corpusculaz(n)
X = zeros(n, Nt)
X[:,1] = x0 .+ σ*randn(n)
for j in 2:Nt, i in 1:n
U = ħ/(2m*dx) * imag( ( ψ(X[i,j-1]+dx, j) - ψ(X[i,j-1]-dx, j) ) / ψ(X[i,j-1], j) )
X[i,j] = X[i,j-1] - U*dt
end
X
end
@time X = corpusculaz(20);
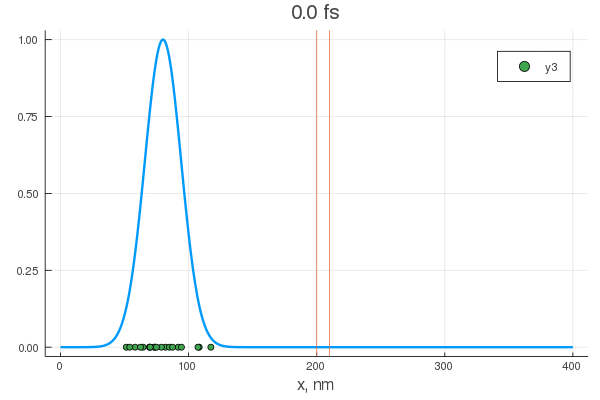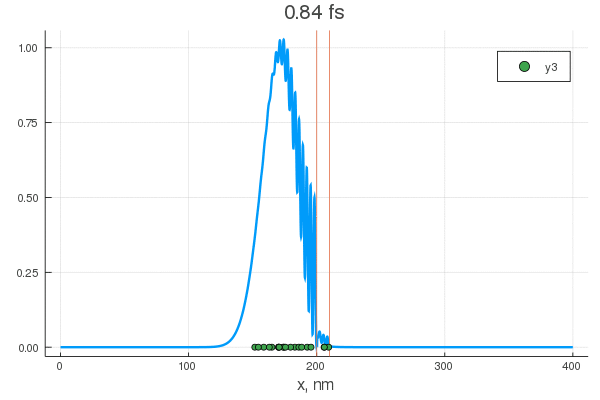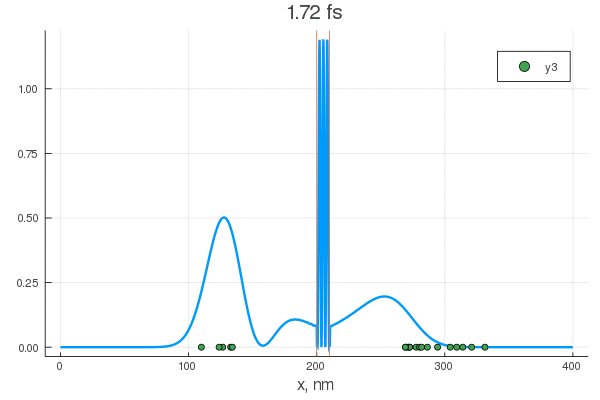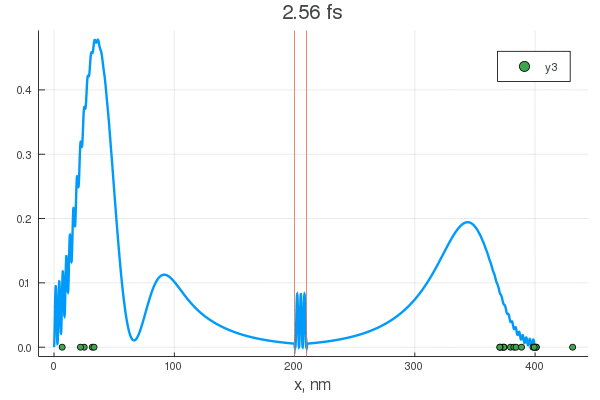
plot(x, P[:, 1], legend = false)
plot!(x, P[:, 80], legend = false)
scatter!( X[:,1], zeros(20) )
scatter!( X[:,80], zeros(20) )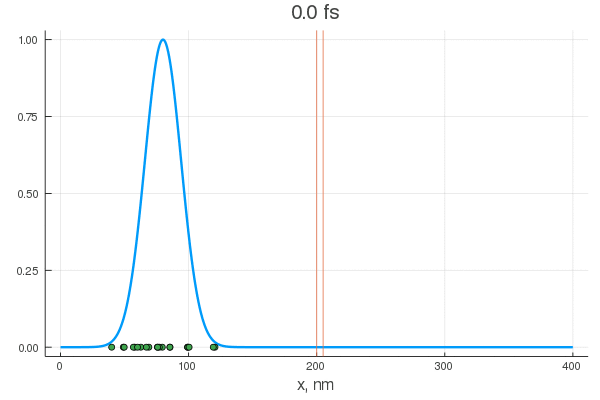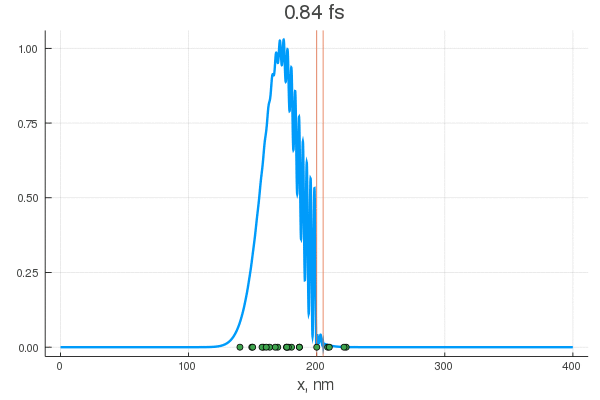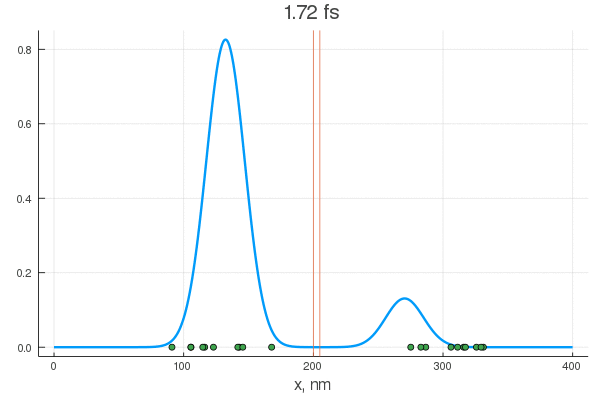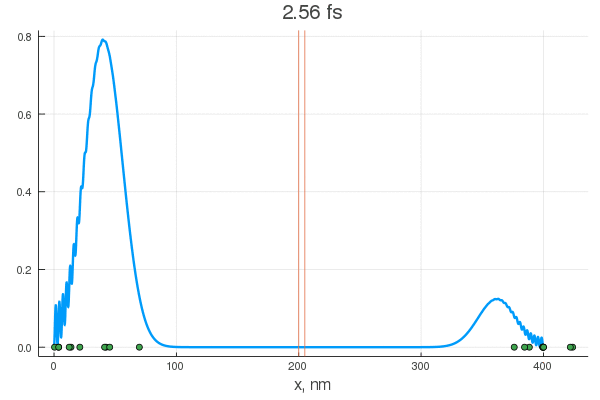
. — , . :
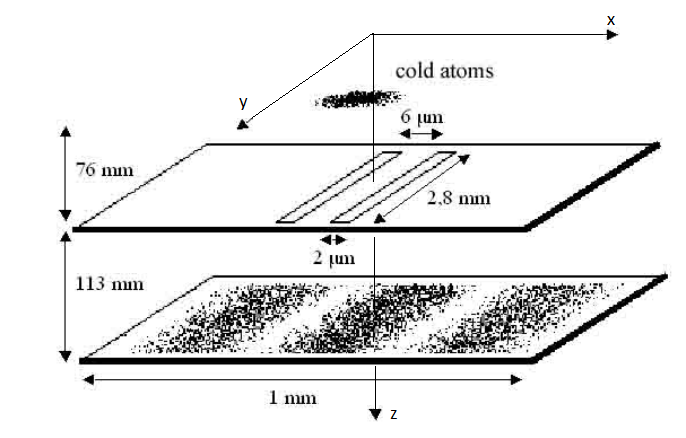
, . Double-slit interference with ultracold metastable neon atoms — - .
using Random, Gnuplot, Statistics
#
function trapez(f, a, b, n)
h = (b - a)/n
result = 0.5*(f(a) + f(b))
for i in 1:n-1
result += f(a + i*h)
end
result * h
end
#
function rk4(f, x, y, h)
k1 = h * f(x , y )
k2 = h * f(x + 0.5h, y + 0.5k1)
k3 = h * f(x + 0.5h, y + 0.5k2)
k4 = h * f(x + h, y + k3)
return y + (k1 + 2*(k2 + k3) + k4)/6.0
endconst ħ = 1.055e-34 # J*s
const kB = 1.381e-23 # J*K-1
const g = 9.8 # m/s^2
const l1 = 76e-3 # m
const l2 = 113e-3 # m
const yh = 2.8e-3 # m
const d = 6e-6 # m
const b = 2e-6 # m
const a1 = 0.5(- d - b) #
const a2 = 0.5(- d + b)
const b1 = 0.5( d - b)
const b2 = 0.5( d + b)
const m = 3.349e-26 # kg
const T = 2.5e-3 # K
const σv = sqrt(kB*T/m) #
const σ₀ = 10e-6 # 10 mkm #
const σz = 3e-4 # 0.3 mm # z
const σk = m*σv / (ħ*√3) # 2e8 m/s #
v₀ = zeros(3)
k₀ = zeros(3);: , , -, .
k
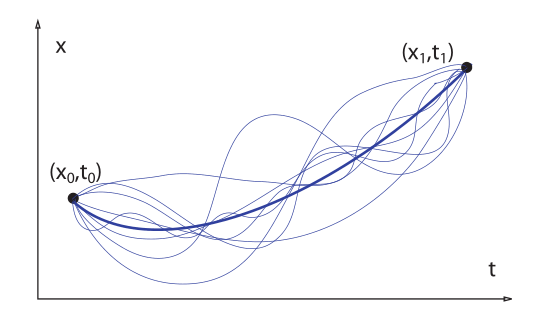
, . , , — . , , , . , , .
Quantum Mechanics And Path Integrals, A. R. Hibbs, R. P. Feynman, , 3.6 .
,
Z , . ,
, . , X, . :
, :
ε₀(t) = σ₀^2 + ( ħ/(2m*σ₀) * t )^2 + (ħ*t*σv/m)^2
s₀(t) = σ₀ + im*ħ/(2m*σ₀) * t
ρₓ(x, t) = exp( -x^2 / (2ε₀(t)) ) / sqrt( 2π*ε₀(t) )
t₁(v, z) = sqrt( 2*(l1-z)/g + (v/g)^2 ) - v/g
tf1 = t₁(v₀[3], 0) # s #
X1 = range(-100, stop = 100, length = 100)*1e-6
Z1 = range(0, stop = l1, length = 100)
Cron1 = range(0, stop = tf1, length = 100)
P1 = [ ρₓ(x, t) for t in Cron1, x in X1 ]
P1 /= maximum(P1); #
@gp "set title 'Wavefun before the slits'" xlab="Z, mkm" ylab="X, mkm"
@gp :- 1000Z1 1000000X1 P1 "w image notit"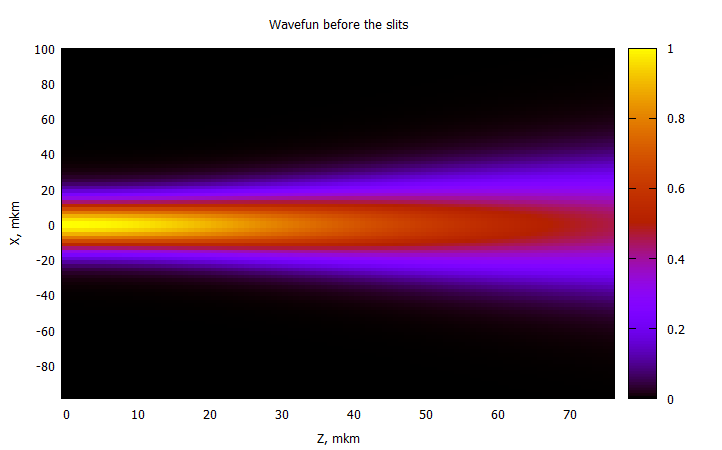
— .
, :
function ρₓ(xᵢ, tᵢ)
Kₓ(xb, tb, xa, ta) = sqrt( m/(2im*π*ħ*(tb-ta)) ) * exp( im*m*(xb-xa)^2 / (2ħ*(tb-ta)) )
function subintrho(k)
ψₓ(x, t) = ( 2π*s₀(t) )^-0.25 * exp( -(x-ħ*k*t/m)^2 / (4σ₀*s₀(t)) + im*k*(x-ħ*k*t/m) )
subintpsi(x) = Kₓ(xᵢ, tᵢ, x, tf1) * ψₓ(x, tf1)
ψa = trapez(subintpsi, a1, a2, 200)
ψb = trapez(subintpsi, b1, b2, 200)
exp( -k^2 / (2σv^2) ) * abs2(ψa + ψb)
end
trapez(subintrho, -10σk, 10σk, 20) / sqrt( 2π*σv^2 )
endt₂(v, z) = sqrt( 2*(l1+l2-z)/g + (v/g)^2 ) - v/g
tf2 = t₂(v₀[3], 0) # s #
X2 = range(-800, stop = 800, length = 200)*1e-6
Z2 = range(l1, stop = l2, length = 100)
Cron2 = range(tf1, stop = tf2, length = 100)
@time P2 = [ ρₓ(x, t) for t in Cron2, x in X2 ];
P2 /= maximum(P2[4:end,:]);
@gp "set title 'Wavefun after the slits'" xlab="t, s" ylab="X, mkm"
@gp :- Cron2[4:end] 1000000X2 P2[4:end,:] "w image notit"2 :
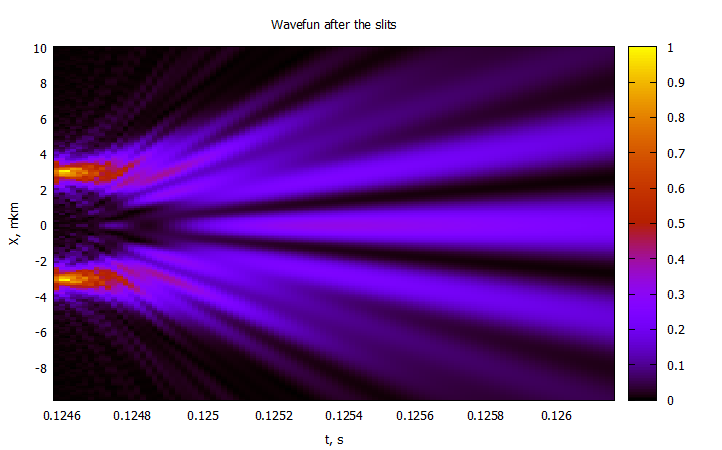
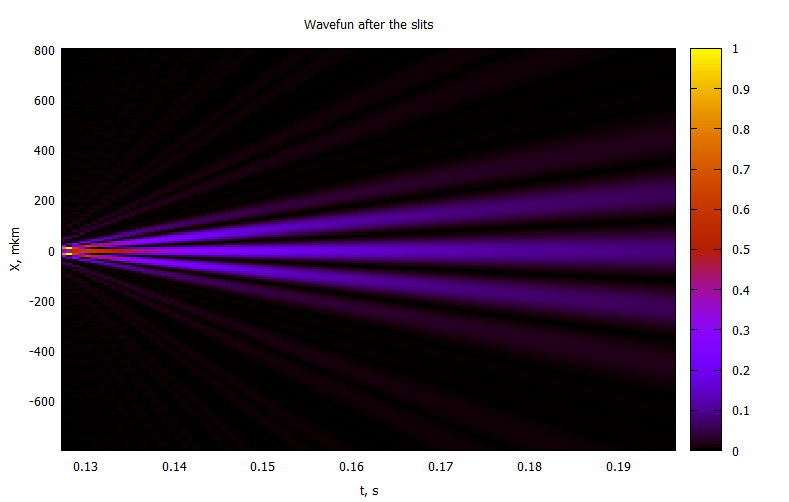
:
, ,
function xbs(t, xo, yo, vo)
cosϕ = xo / sqrt( xo^2 + yo^2 )
sinϕ = yo / sqrt( xo^2 + yo^2 )
atnx = -ħ*t / (2m*σ₀^2)
sinatnx = atnx / sqrt( atnx^2 + 1)
cosatnx = 1 / sqrt( atnx^2 + 1)
cosϕt = cosϕ * cosatnx - sinϕ * sinatnx
#sinϕt = sinϕ*cosatnx + cosϕ*sinatnx
σ₀t = sqrt( σ₀^2 + ( ħ*t / (2*m*σ₀) )^2 )
vo*t + sqrt(xo^2 + yo^2) * σ₀t/σ₀ * cosϕt
end
@gp "set title 'Trajectories before slits'" xlab="t, s" ylab="X, mkm" # "set yrange [-10:10]"
@time for i in 1:80
x0 = randn()*σ₀
y0 = randn()*σ₀
v0 = randn()*σv*1e-4
prtclᵢ = [ xbs(t,x0,y0,v0) for t in Cron1 ]
@gp :- Cron1 1000000prtclᵢ "with lines notit lw 2 lc rgb 'black'"
# slits -4-> -2, 2->4 mkm
end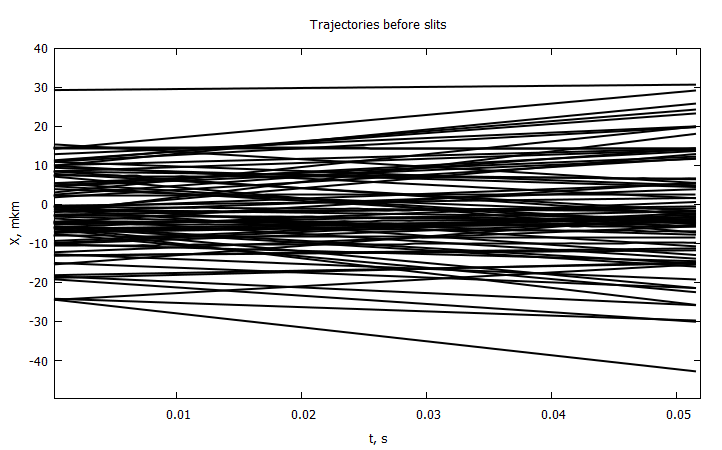
, , , , , . . . , .
Y , , . X . .
" " ,
function Uₓ(t, x)
γ = -m*x / ( ħ*(t-tf1) )
β = m/(2ħ) * ( 1/(t-tf1) + 1 / ( tf1*( 1 + (2m*σ₀^2 / (ħ*tf1) )^2 ) ) )
α = -( 4σ₀^2 * ( 1 + ( ħ*tf1 / (2m*σ₀^2) )^2 ) )^-1
f(x, u, t) = exp( ( α + im*β )*u^2 + im*γ*u )
C = f(x, a2, t) - f(x, a1, t) + f(x, b2, t) - f(x, b1, t)
H = trapez( u-> f(x, u, t) , a1, a2, 400) + trapez( u-> f(x, u, t) , b1, b2, 400)
return 1/(t-tf1) * ( x - 0.5/(α^2 + β^2) * ( β*imag(C/H) + α*real(C/H) - β*γ ) )
end
init() = bitrand()[1] ? rand()*(b2 - b1) + b1 : rand()*(a2 - a1) + a1
myrng(a, b, N) = collect( range(a, stop = b, length = N ÷ 2) )
n = 1
xx = 0
ξ = 1e-5
while xx < Cron2[end]-Cron2[1]
n+=1
xx += (ξ*n)^2
end
n
steps = [ (ξ*i)^2 for i in 1:n1 ]
Cronadapt = accumulate(+, steps, init = Cron2[1] )
function modelsolver(Np = 10, Nt = 100)
#xo = [ init() for i = 1:Np ] #
xo = vcat( myrng(a2, a1, Np), myrng(b1, b2, Np) ) #
xpath = zeros(Nt, Np)
xpath[1,:] = xo
for i in 2:Nt, j in 1:Np
xpath[i,j] = rk4(Uₓ, Cronadapt[i], xpath[i-1,j], steps[i] )
end
xpath
end@time paths = modelsolver(20, n);
@gp "set title 'Trajectories after the slits'" xlab="t, s" ylab="X, mkm" "set yrange [-800:800]"
for i in 1:size(paths, 2)
@gp :- Cronadapt 1e6paths[:,i] "with lines notit lw 1 lc rgb 'black'"
end- 4 , . 2
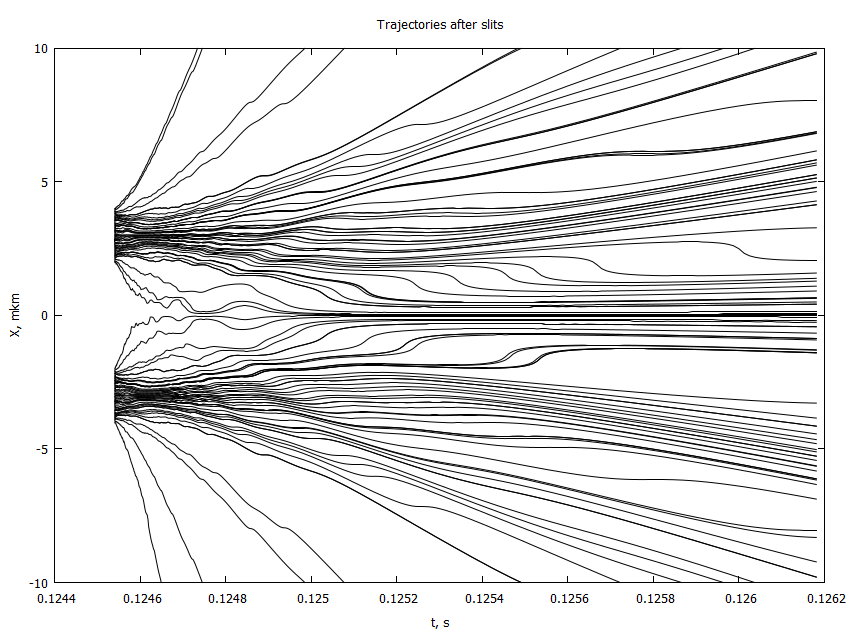
, : , , .
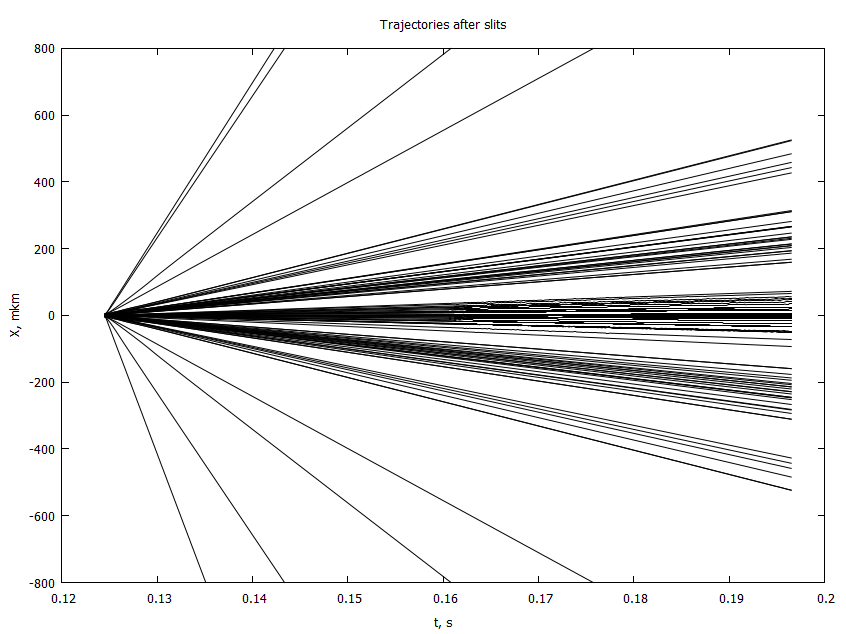
. , ,
function yas(t, xo, yo, vo)
cosϕ = xo / sqrt( xo^2 + yo^2 )
sinϕ = yo / sqrt( xo^2 + yo^2 )
atnx = -ħ*t / (2m*σ₀^2)
sinatnx = atnx / sqrt( atnx^2 + 1)
cosatnx = 1 / sqrt( atnx^2 + 1)
#cosϕt = cosϕ * cosatnx - sinϕ * sinatnx
sinϕt = sinϕ*cosatnx + cosϕ*sinatnx
σ₀t = sqrt( σ₀^2 + ( ħ*t / (2*m*σ₀) )^2 )
vo*t + sqrt(xo^2 + yo^2) * σ₀t/σ₀ * sinϕt
end
function modelsolver2(Np = 10)
Nt = length(Cronadapt)
xo = [ init() for i = 1:Np ]
#xo = vcat( myrng(a2, a1, Np), myrng(b1, b2, Np) )
xcoord = copy(xo)
ycoord = zeros(Np)
for i in 2:Nt, j in 1:Np
xcoord[j] = rk4(Uₓ, Cronadapt[i], xcoord[j], steps[i] )
end
for (i, x) in enumerate(xo)
y0 = randn()*yh
v0 = 0 #randn()*σv*1e-4
ycoord[i] = yas(Cronadapt[end], x, y0, v0)
end
xcoord, ycoord
end
@time X, Y = modelsolver2(100);
@gp "set title 'Impacts on the screen'" xlab="X, mm" ylab="Y, mm"# "set xrange [-1:1]"
@gp :- 1000X 1000Y "with points notit pt 7 ps 0.5 lc rgb 'black'"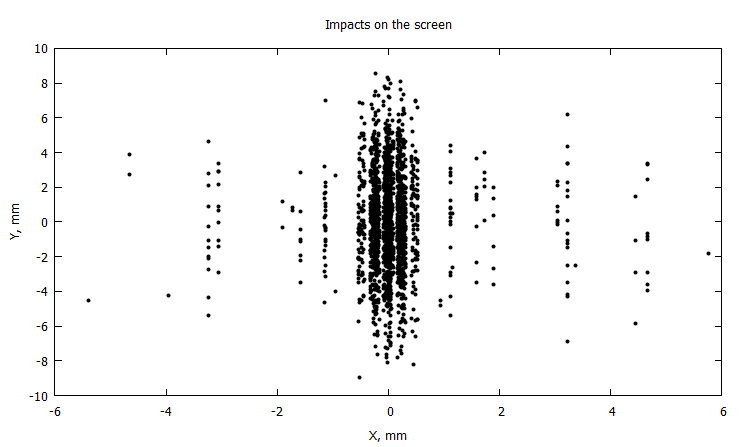
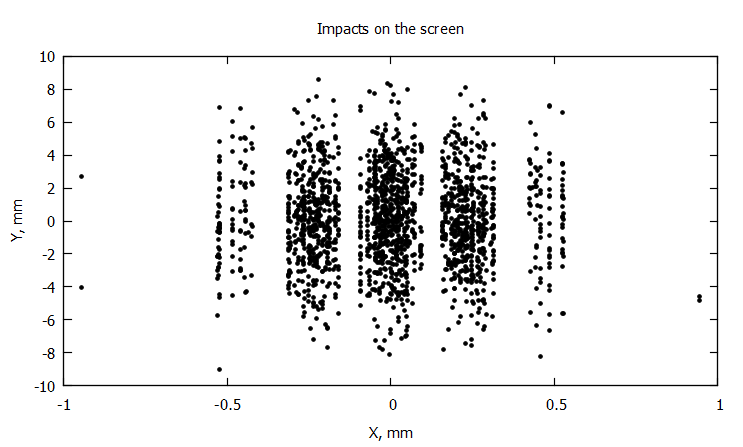
, , . , ,