5 خوارزميات انحدار تعلم الآلة يجب أن تعرفها

المصدر: Vecteezy



نعم ، الانحدار الخطي ليس هو الوحيد.



بسرعة تسمية خمس خوارزميات التعلم الآلي.



من غير المحتمل أن تسمي العديد من خوارزميات الانحدار. بعد كل شيء ، فإن خوارزمية الانحدار الوحيدة المستخدمة على نطاق واسع هي الانحدار الخطي ، ويرجع ذلك أساسًا إلى بساطتها. ومع ذلك ، غالبًا ما يكون الانحدار الخطي غير قابل للتطبيق على البيانات الحقيقية بسبب الخيارات المحدودة للغاية وحرية المناورة المحدودة. غالبًا ما يستخدم فقط كنموذج أساسي للتقييم والمقارنة مع مناهج البحث الجديدة.



فريق حلول سحابة Mail.ruترجم مقالاً يصف مؤلفه 5 خوارزميات انحدار. إنها تستحق وجودها في صندوق الأدوات الخاص بك جنبًا إلى جنب مع خوارزميات التصنيف الشائعة مثل SVM وشجرة القرار والشبكات العصبية.

1. انحدار الشبكة العصبية

نظرية

الشبكات العصبية قوية بشكل لا يصدق ، لكنها تستخدم عادة في التصنيف. تنتقل الإشارات عبر طبقات من الخلايا العصبية ويتم تلخيصها في فئة واحدة من عدة فئات. ومع ذلك ، يمكن تكييفها بسرعة كبيرة في نماذج الانحدار عن طريق تغيير وظيفة التنشيط الأخيرة.



ينقل كل خلية عصبية القيم من الاتصال السابق من خلال وظيفة التنشيط التي تخدم غرض التعميم واللاخطية. عادة ما تكون وظيفة التنشيط شيء مثل السيني أو وظيفة ReLU (وحدة خطية مصححة).





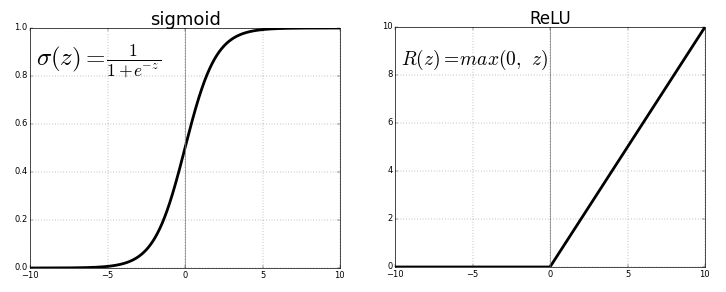
المصدر . صورة مجانية



ولكن ، استبدال وظيفة التنشيط الأخيرة (العصبون الناتج) بوظيفة خطيةوظيفة التنشيط ، يمكن تعيين إشارة الخرج إلى العديد من القيم خارج الفئات الثابتة. وبالتالي ، لن يكون الناتج هو احتمال تعيين إشارة الإدخال إلى أي فئة واحدة ، ولكن القيمة المستمرة التي تصلح بها الشبكة العصبية ملاحظاتها. بهذا المعنى ، يمكننا القول أن الشبكة العصبية تكمل الانحدار الخطي.



يتمتع انحدار الشبكة العصبية بميزة اللاخطية (بالإضافة إلى التعقيد) التي يمكن تقديمها مع وظائف التنشيط السيني وغيرها من وظائف التنشيط غير الخطية في وقت سابق في الشبكة العصبية. ومع ذلك ، قد يعني الإفراط في استخدام ReLU كوظيفة تنشيط أن النموذج يميل إلى تجنب إخراج القيم السالبة ، لأن ReLU يتجاهل الاختلافات النسبية بين القيم السلبية.



يمكن حل هذا إما عن طريق تقييد استخدام ReLU وإضافة المزيد من القيم السلبية لوظائف التنشيط المقابلة ، أو عن طريق تطبيع البيانات إلى نطاق إيجابي صارم قبل التدريب.

التنفيذ

باستخدام Keras ، دعنا نبني بنية شبكة عصبية اصطناعية ، على الرغم من أنه يمكن فعل الشيء نفسه مع شبكة عصبية تلافيفية أو شبكة أخرى إذا كانت الطبقة الأخيرة إما طبقة كثيفة مع تنشيط خطي أو مجرد طبقة ذات تنشيط خطي. ( لاحظ أن واردات Keras غير مدرجة لتوفير مساحة ).

model = Sequential()

model.add(Dense(100, input_dim=3, activation='sigmoid'))

model.add(ReLU(alpha=1.0))

model.add(Dense(50, activation='sigmoid'))

model.add(ReLU(alpha=1.0))

model.add(Dense(25, activation='softmax'))



#IMPORTANT PART

model.add(Dense(1, activation='linear'))



لطالما كانت مشكلة الشبكات العصبية هي تباينها الكبير وميلها إلى الإفراط في الاستخدام. هناك العديد من مصادر اللاخطية في مثال الكود أعلاه مثل SoftMax أو السيني.



إذا كانت شبكتك العصبية تقوم بعمل جيد مع بيانات التدريب ببنية خطية بحتة ، فقد يكون من الأفضل استخدام انحدار شجرة القرار المبتور ، والذي يحاكي شبكة عصبية خطية ومشتتة للغاية ، ولكنه يسمح لعالم البيانات بالتحكم بشكل أفضل في العمق والعرض والسمات الأخرى للتحكم في التخصيص.

2. انحدار شجرة القرار

نظرية

تتشابه أشجار القرار في التصنيف والانحدار إلى حد بعيد من حيث أنها تعمل من خلال إنشاء أشجار ذات عقد بنعم / لا. ومع ذلك ، بينما ينتج عن العقد الطرفية للتصنيف قيمة فئة واحدة (على سبيل المثال ، 1 أو 0 لمشكلة تصنيف ثنائي) ، ينتهي الأمر بأشجار الانحدار بقيمة في الوضع المستمر (على سبيل المثال ، 4593.49 أو 10.98).





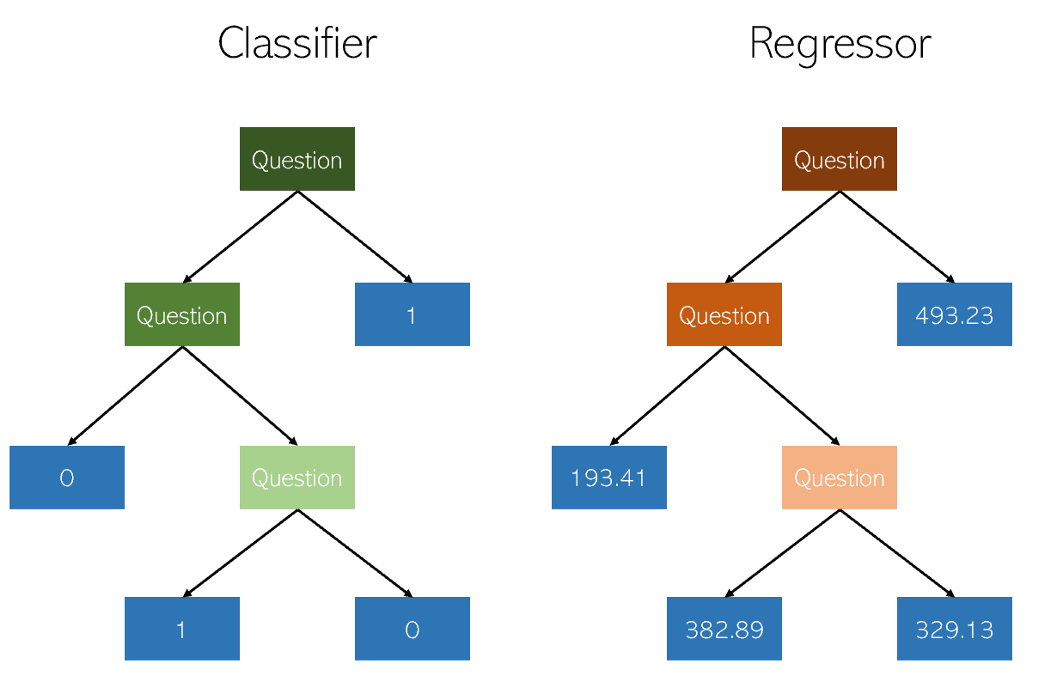
رسم توضيحي للمؤلف



نظرًا لطبيعة الانحدار المحددة والمشتتة بشكل كبير كمشكلة بسيطة للتعلم الآلي ، يجب تقليم رجوع شجرة القرار بعناية. ومع ذلك ، فإن نهج الانحدار غير منتظم - بدلاً من حساب القيمة على مقياس مستمر ، فإنه يصل إلى العقد النهائية المحددة. إذا تم قص الانحدار كثيرًا ، فهذا يعني أنه يحتوي على عدد قليل جدًا من العقد الورقية للوفاء بالغرض منه بشكل صحيح.



وبالتالي ، يجب تقليم شجرة القرار بحيث تتمتع بأكبر قدر من الحرية (قيم الإخراج المحتملة للانحدار هي عدد العقد الورقية) ، ولكن ليس بما يكفي لتكون عميقة جدًا. إذا لم تقم بقطعها ، فستصبح الخوارزمية شديدة التشتت بالفعل معقدة للغاية بسبب طبيعة الانحدار.

التنفيذ

يمكن إنشاء انحدار شجرة القرار بسهولة في sklearn:

from sklearn.tree import DecisionTreeRegressor
model = DecisionTreeRegressor()
model.fit(X_train, y_train)

نظرًا لأن معاملات رجوع شجرة القرار مهمة جدًا ، يوصى باستخدام معلمات أداة تحسين محرك البحث GridCVمن sklearn، للعثور على التوصية الصحيحة لهذا النموذج.



عند تقييم الأداء رسميًا ، استخدم الاختبار K-foldبدلاً من الاختبار القياسي train-test-splitلتجنب عشوائية الأخير التي قد تنتهك النتائج الحساسة لنموذج التباين العالي.



علاوة: يمكن أيضًا تطبيق خوارزمية الغابة العشوائية ، وهي قريبة من شجرة القرار ، كعامل تراجع. قد يكون أداء الانحدار العشوائي للغابات أفضل من شجرة القرار في الانحدار وقد لا يكون كذلك (بينما يؤدي عادةً أداءً أفضل في التصنيف) بسبب التوازن الدقيق بين التكرار والنقص في طبيعة خوارزميات بناء الشجرة.

from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor()
model.fit(X_train, y_train)

3. انحدار اللاسو

انحدار Lasso (LASSO ، Least Absolute Shrinkage and Selection Operator) هو تباين في الانحدار الخطي الذي تم تكييفه خصيصًا للبيانات التي تظهر ارتباطًا وثيقًا متعدد الخطوط (أي الارتباط القوي للميزات مع بعضها البعض).



يقوم بأتمتة أجزاء من اختيار النموذج مثل الاختيار المتغير أو استبعاد المعلمات. يستخدم LASSO الانكماش ، وهو عملية تقترب فيها قيم البيانات من نقطة مركزية (مثل المتوسط).





رسم توضيحي للمؤلف. تصور مبسط



لعملية الضغط تضيف عملية الضغط مزايا عديدة لنماذج الانحدار:

• تقديرات أكثر دقة واستقرارًا للمعلمات الحقيقية.
• التقليل من أخطاء أخذ العينات ونزع العينات
• تهدئة التقلبات المكانية.

بدلاً من تعديل تعقيد النموذج للتعويض عن تعقيد البيانات ، مثل الشبكة العصبية عالية التباين وطرق انحدار شجرة القرار ، يحاول اللاسو تقليل تعقيد البيانات بحيث يمكن التعامل معها من خلال طرق الانحدار البسيطة عن طريق تقويس المساحة التي تقع عليها. في هذه العملية ، يساعد اللاسو تلقائيًا في إزالة أو تشويه الميزات المترابطة والمتكررة في طريقة التباين المنخفض.



يستخدم انحدار Lasso تنظيم L1 ، أي يزن الأخطاء بقيمتها المطلقة. بدلاً من ، على سبيل المثال ، تنظيم L2 ، الذي يزن الأخطاء بمربعها ، من أجل معاقبة الأخطاء الأكثر أهمية بشكل أقوى.



غالبًا ما يؤدي هذا التنظيم إلى نماذج متناثرة ذات معاملات أقل ، حيث قد تصبح بعض المعاملات صفرية وبالتالي يتم استبعادها من النموذج. هذا يسمح بتفسيرها.

التنفيذ

و sklearnالانحدار تأتي اسو مع نموذج عبر التحقق من صحة الذي يختار الأكثر فعالية من العديد من النماذج تدرب مع الثوابت الأساسية المختلفة ومسارات التعلم بأتمتة مهمة من شأنها أن يكون على خلاف ذلك لأداء يدويا.

from sklearn.linear_model import LassoCV
model = LassoCV()
model.fit(X_train, y_train)

4. انحدار ريدج (ريدج انحدار)

نظرية

انحدار ريدج أو انحدار التلال يشبه إلى حد بعيد انحدار لاسو من حيث أنه يطبق الضغط. كلا الخوارزميتين مناسبتان تمامًا لمجموعات البيانات التي تحتوي على عدد كبير من الميزات غير المستقلة عن بعضها البعض (علاقة خطية متداخلة).



ومع ذلك ، فإن الاختلاف الأكبر بينهما هو أن انحدار التلال يستخدم التنظيم L2 ، أي أن أيا من المعاملات لا يصبح صفرا ، كما هو الحال مع انحدار LASSO. بدلاً من ذلك ، تقترب المعاملات بشكل متزايد من الصفر ، ولكن ليس لديها حافزًا كبيرًا لتحقيق ذلك بسبب طبيعة تنظيم L2.





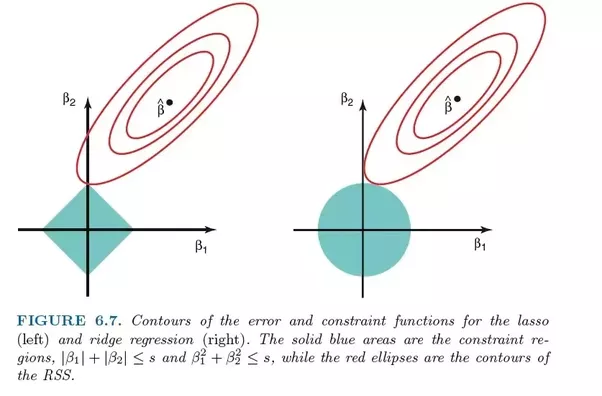
مقارنة الأخطاء في انحدار لاسو (يسار) وانحدار التلال (يمين). نظرًا لأن Ridge Regression يستخدم تنظيم L2 ، فإن منطقته تشبه الدائرة ، بينما يرسم تنظيم L1 lasso خطوطًا مستقيمة. صورة مجانية. المصدر



في lasso ، يتم ترجيح التحسن من الخطأ 5 إلى الخطأ 4 بنفس طريقة ترجيح التحسين من 4 إلى 3 ، وكذلك من 3 إلى 2 ، ومن 2 إلى 1 ومن 1 إلى 0. لذلك ، يصل المزيد من المعاملات إلى الصفر ويتم التخلص من المزيد من الميزات.



ومع ذلك ، في انحدار التلال ، يتم حساب التحسن من الخطأ 5 إلى الخطأ 4 على أنه 5² - 4² = 9 ، بينما يتم ترجيح التحسن من 4 إلى 3 على أنه 7. تدريجيًا ، تنخفض مكافأة التحسين ؛ لذلك ، يتم التخلص من ميزات أقل.



انحدار ريدج هو الأنسب للحالات التي نريد فيها ترتيب عدد كبير من المتغيرات حسب الأولوية ، ولكل منها تأثير ضئيل. إذا احتاج نموذجك إلى حساب متغيرات متعددة ، لكل منها تأثير متوسط ​​إلى كبير ، فإن lasso هو الخيار الأفضل.

التنفيذ

sklearnيمكن تنفيذ انحدار ريدج على النحو التالي (انظر أدناه). كما هو الحال مع انحدار اللاسو ، sklearnهناك تطبيق للتحقق من صحة اختيار أفضل النماذج المدربة.

from sklearn.linear_model import RidgeCV
model = Ridge()
model.fit(X_train, y_train)

5. انحدار ElasticNet

نظرية

يهدف ElasticNet إلى الجمع بين أفضل ما في Ridge Regression و Lasso Regression من خلال الجمع بين تنظيم L1 و L2.



Lasso و Ridge Regression طريقتان مختلفتان للتنظيم. في كلتا الحالتين ، λ هو العامل الأساسي الذي يتحكم في حجم الغرامة:

1. λ = 0, , .
2. λ = ∞, - . , , .
3. 0 < λ < ∞, λ , .

إلى المعلمة λ ، يضيف انحدار ElasticNet معلمة إضافية α ، والتي تقيس كيفية "خلط" التوحيدات L1 و L2. عندما تكون α تساوي 0 ، يكون النموذج هو انحدار التلال الخالص ، وعندما تكون α هي 1 ، يكون انحدار لاسو خالص.



يحدد "عامل الخلط" α ببساطة مقدار تنظيم L1 و L2 الذي يجب مراعاته في دالة الخسارة. تهدف نماذج الانحدار الثلاثة الشائعة - Ridge و Lasso و ElasticNet - إلى تقليل حجم معاملاتها ، لكن كل منها يعمل بشكل مختلف.

التنفيذ

يمكن تنفيذ ElasticNet باستخدام نموذج التحقق عبر sklearn:

from sklearn.linear_model import ElasticNetCV
model = ElasticNetCV()
model.fit(X_train, y_train)

ماذا تقرأ عن الموضوع:

1. تحليل البيانات الضخمة في السحابة: كيف يمكن أن تصبح الأعمال قائمة على البيانات.
2. تنسيقات الملفات في البيانات الضخمة.
3. - .