لم أفهم مشكلة جولدباخ

اليوم أريد أن أخبركم كيف حاولت حل مشكلة Goldbach

. مشكلة Goldbach هي القول بأن أي عدد زوجي ، بدءًا من 4 ، يمكن تمثيله كمجموع اثنين من الأعداد الأولية. أي 6 = 3 + 3 ؛ 8 = 5 + 3 ... كما أفهمها ، فإن حل المشكلة هو إثبات أو دحض هذه العبارة.



أول شيء يتعين علينا القيام به هو تنفيذ طريقة للتحقق مما إذا كان الرقم أوليًا. أولي هو عدد لا يقبل القسمة إلا على نفسه وعلى واحد.

public static bool IsPrimeNumber(ulong n)
{
    var result = true;
    if (n > 1)
    {
        for (ulong i = 2; i < n; i++)
        {
           if (n % i == 0)
           {
                result = false;
                break;
            }
        }
    }
    else
    {
        result = false;
    }
    return result;
}

نحتاج الآن إلى الحصول على مجموعة من جميع الأعداد الأولية حتى ulong.MaxValue = 18446744073709551615 (2 ^ 64-1)

public static IEnumerable<ulong> GetAllPrimeNumbers(ulong maxNumber)
{
    List<ulong> primeNumbers = new List<ulong>();
    for (ulong i=0; i < maxNumber; i++ )
    {
        if (IsPrimeNumber(i))
        {
            primeNumbers.Add(i);
        }
    }
    return primeNumbers;
}

يقترح الحدس أن حسابهم سيستغرق وقتًا طويلاً ، لذلك سنقلل عددهم إلى 300000

static void Main(string[] args)
{
    Stopwatch stopwatch = new Stopwatch();
    stopwatch.Start();
    IEnumerable<ulong> primeNumbers = GetAllPrimeNumbers();
    checkGoldbach(primeNumbers); 
    stopwatch.Stop();
    Console.WriteLine("  " + stopwatch.Elapsed.TotalSeconds + " ");
    foreach(var number in primeNumbers)
    {
        Console.Write(number + " ");
    }
    Console.ReadKey();
}

ثم أردت العثور على جميع الأعداد الأولية حتى 2 ^ 64 (بدا لي أن بضع ساعات من الحسابات ستكون كافية بالنسبة لي)

بعد دقيقتين من تشغيل البرنامج ، قررت وضع نقطة توقف والتحقق من الرقم الذي يتم فحصه من أجل البساطة:



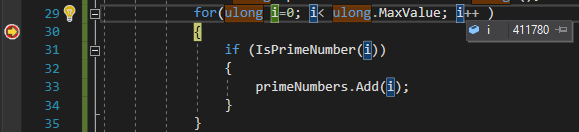
411780 تكرار بعد دقيقتين من العمليات الحسابية. قررت تحسين طريقة التحقق من بساطة الرقم بشكل طفيف ، حيث لا توجد حاجة لمواصلة التكرار بعد نصف الرقم



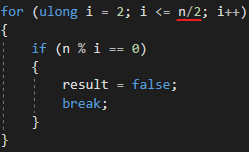
، وبالتالي ، تم تقليل عدد التكرارات المطلوبة للتحقق من البساطة إلى النصف. بدا لي أنه في غضون دقيقتين يجب أن يتضاعف عدد التكرارات



لكن هنا أيضًا كنت مخطئًا. لم تزد الإنتاجية بنسبة 100٪ بل بنسبة 22٪. كما فهمت لاحقًا ، يرجع هذا إلى حقيقة أن نصف الشيكات ، كما كان من قبل ، يتم حذفها عن طريق القسمة على 2 ، ويتم التخلص من ثلث جميع الأرقام التي لم يتم حذفها بالقسمة على 2 بالقسمة على 3 ، إلخ. تم العثور على 41549 اختبارًا أوليًا من بين 500154 اختبارًا أوليًا. هذا هو للتكرار

for (ulong i = 2; i <= n/2; i++)
{
    if (n % i == 0)
    {
        result = false;
        break;
    }
}

تم تنفيذه حتى النهاية (بدون انقطاع) 41549 مرة فقط. في حالات أخرى ، تمت مقاطعته في وقت سابق ...

500154 وليس تقريبًا 2 ^ 64 ، تحتاج إلى حساب المدة التي ستستغرقها للتحقق من بساطة جميع الأرقام إلى 2 ^ 64

أولاً ، دعنا نخفض عدد التكرارات من 2 ^ 64 إلى 30000 ونحسب وقت تشغيل طريقة ساعة الإيقاف



للتكرار. أرقام تصل إلى 30000 ، تم إنفاق ثانية واحدة

الآن ، فلنقم بإنشاء جدول بقيم أخرى لعدد التكرارات ، فلنكتب



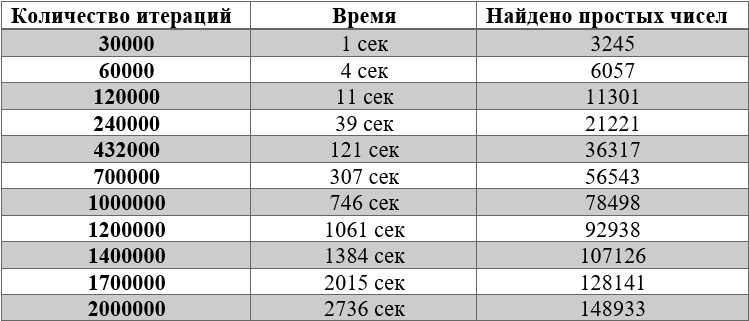
النتيجة في Excel ، وننشئ رسمًا بيانيًا نقطيًا للإحداثيات "عدد التكرارات للوقت" و "عدد الأعداد الأولية لكل نطاق"





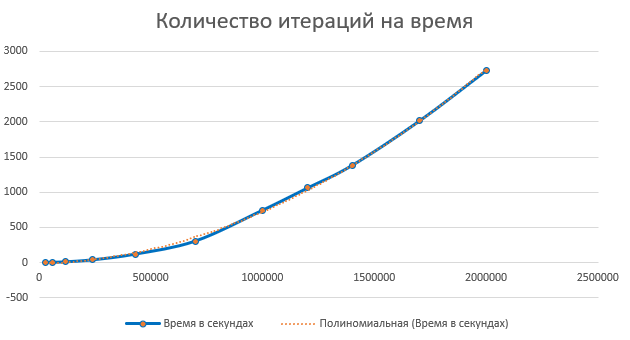
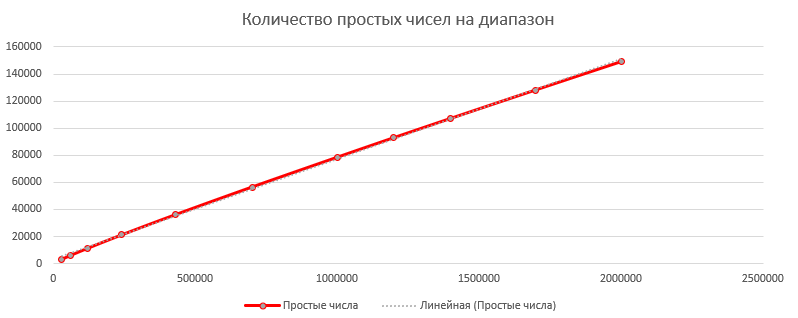
الآن يمكننا معرفة العدد التقريبي للأعداد الأولية حتى 2 ^ 64 ، وتقريبًا كم سيستغرق العثور عليهم جميعًا

إذا أضفت خط اتجاه "خطي" إلى الرسم البياني "الأعداد الأولية لكل نطاق" ، فسيعطيك Excel الصيغة y = 0.074x + 3004 (لا أعرف مدى دقة الصيغة). هذا يعني أن العدد التقريبي للأعداد الأولية حتى ulong.MaxValue = 0.074 * 2 ^ 64 + 3004 ؛

بالطريقة نفسها ، بإضافة خط الاتجاه "متعدد الحدود" إلى مخطط "عدد التكرارات بمرور الوقت" ، نحصل على الصيغة y = 7E-10x2 + 6E-05x. باستبدال رقمنا 2 ^ 64 بدلاً من x ، يمكنك معرفة أنه للعثور على جميع الأعداد الأولية حتى 2 ^ 64 ، نحتاج إلى 2.38E + 29 ثانية تقريبًا ، أو 7553198149564240000000 سنة. حسنًا ، لا يمكنني توقع ذلك كثيرًا.

دعنا نحاول إثبات أن تخمين جولدباخ صحيح لجميع الأعداد الزوجية حتى 300000.

public static void checkGoldbach(IEnumerable<ulong> primeNumbers)
{
    ulong numbersCount = 300000;
    for (ulong number = 4; number<numbersCount; number+=2)
    {
        bool isGoldbachResult = false;
        foreach(ulong primeNumber1 in primeNumbers)
        {
            foreach(ulong primeNumber2 in primeNumbers)
            {
                if(primeNumber1+primeNumber2==number)
                {
                    Console.WriteLine("{0} = {1} + {2}", number, primeNumber1, primeNumber2);
                    isGoldbachResult = true;
                    break;
                }
                if(primeNumber1+primeNumber2>number)
                {
                    break;
                }
            }
            if(isGoldbachResult|| primeNumber1>number)
            {
                break;
            }
        }
        if(!isGoldbachResult)
        {
            Console.WriteLine(" " + number + "         ");
            break;
        }
    }
}

إذا كانت عبارة Goldbach غير صحيحة بالنسبة لبعض الأرقام ، فستتوقف الطريقة عن الحساب عند هذا الرقم.



بعد 9 دقائق من العمليات الحسابية ، يمكننا القول أن فرضية Goldbach صالحة للأعداد الأقل من 300000.

مجموع

اتضح أن كل شيء لم يكن بهذه البساطة كما بدا لي في البداية ، وأدرك أنني لست قريبًا على الإطلاق من حل المشكلة.

على الأرجح ، يبدو لي أن هناك خيارات أفضل للتحقق من رقم للبساطة. من المحتمل أن الطريقة التي تتحقق من الأرقام الزوجية لصحة بيان جولدباخ يمكن تنفيذها بطريقة عقلانية أكثر من مجرد تعداد بسيط للأعداد الأولية ، لكنني لم أعد أرغب في قضاء الكثير من الوقت في هذا ...

حل مشكلة جولدباخ لن يعطي شيئًا للبشرية. لقد ثبت حتى الآن أن الفرضية صحيحة بالنسبة للأعداد حتى 4 * 10 ^ 18 ، ولكن ما الهدف من إثباتها لجميع الأرقام؟ لأي غرض يكتب علماء الرياضيات كتبًا حول هذا الموضوع ويقضون وقتهم عمومًا في حل مثل هذه "المشكلات"؟

أريد حقًا أن أسأل الأشخاص المطلعين عما إذا كانت الصيغة الخاصة بي لحساب عدد الأعداد الأولية لكل نطاق لها الحق في الوجود؟

ملاحظة

على الأرجح ، لست بحاجة إلى كتابة مقالات لا أعرف عنها إلا القليل. لم أكن أتوقع رد فعل المجتمع بهذه الطريقة. لكني لم أتظاهر بأن الحل الذي قدمته هو الحل الوحيد الصحيح. أنا أحد الهواة في هذا المجال.

لأي غرض كتبت هذا المقال؟

أخذت الوقت الكافي للبحث في هذا السؤال ، وبدا لي أن بعض الناس قد يعجبهم. كانت ممتعة بالنسبة لي لأنها مهمة ممتعة. لكن لماذا يضيع علماء الرياضيات وقتهم في هذا؟ أنا بصدق لا أفهم الفائدة الحقيقية من البحث عن هذه الأسئلة المحددة.

PPS

بعد قراءة المراجعات حول المقال ، قررت استخلاص النتائج.

على الأرجح ، يبدو لي أن هناك خيارات أفضل للتحقق من رقم للبساطة

على النحو الذي اقترحه المستخدمون dvserg drWhy و بافل_الأفضلهو حقا. على سبيل المثال ، باستخدام غربال إراتوستينس ، يمكن جمع مجموعة من الأعداد الأولية بشكل أسرع. فيما يلي المقالات التي يمكنك قراءتها حول هذا الموضوع: خوارزمية للتحقق من البساطة في O (log N) ، ويكيبيديا ، يمكنك قراءة أعمال Srinivas Ramanujan Iyengor

هل الصيغة الخاصة بي لحساب عدد الأعداد الأولية لكل نطاق لها الحق في الوجود؟

لا

حل مشكلة جولدباخ لن يعطي شيئًا للبشرية؟

إن رأيي أن بعض مسائل الرياضيات عديمة الفائدة تسبب في موقف سلبي حاد من معظم المستخدمين. المستخدمونفوادزيم ثلاجة برومز الرسم البياني في ثلاجة EimKR bfDeveloper و نعمكانت قادرة على إقناعي بهذا. أسترجع كلامي.

منذ العصور القديمة ، كان علماء الرياضيات يبحثون عن الحقيقة ، وغالبًا ما يؤدي بحثهم إلى عواقب مفيدة للتقدم. ربما لن تعطي المشكلة نفسها وحلها للعالم أي شيء هنا والآن ، لكنها الاستنتاجات التي تم التوصل إليها أثناء البحث عن حل يمكن أن تكون مفيدة على المدى الطويل.