من القدرة على معالجة كميات هائلة من المعلومات واستخدام خوارزميات التعلم الآلي بشكل أكثر كفاءة ، إلى خوارزميات النمذجة الكمية التي يمكنها تحسين الحسابات (من حيث النوعية والكمية) لتصميم الأدوية الجديدة ، والتنبؤ ببنية البروتين ، وتحليل العمليات المختلفة في الكائن البيولوجي ، و إلخ تخضع هذه المنظورات المحيرة للعقل لضجيج معلومات هائل اليوم ، مما يعني أنه من المهم تسليط الضوء على المحاذير والتحديات في هذه التكنولوجيا الجديدة.
تحذير: تستند المراجعة إلى مقال لمجموعة من الباحثين الأوروبيين من المملكة المتحدة وسويسرا (كارلوس أوتيرال ، مارتن ستراهم ، جي شي ، غاريت إم موريس ، سيمون سي بنجامين ، شارلوت إم دين. "آفاق الحوسبة الكمومية في البيولوجيا الجزيئية الحاسوبية" ، WIREs Computational Molecular Science التي نشرتها Wiley Periodicals LLC ، 2020). لن يتم تضمين أصعب أجزاء المقالة المتعلقة بالنماذج الرياضية المعقدة في المراجعة. لكن المادة معقدة في البداية ، ويطلب من القارئ أن يكون لديه معرفة بالرياضيات وفيزياء الكم.
ولكن إذا كنت تنوي البدء في دراسة تطبيق تقنيات الكم في المعلوماتية الحيوية ، فمن أجل الدخول في الموضوع أولاً ، فأنت مدعو للاستماع إلى حديث قصير من قبل فيكتور سوكولوف ، كبير الباحثين في M&S Decisions ، والذي يوضح بعض المشكلات الحديثة في نمذجة الأدوية:
المقدمة
منذ ظهور الحوسبة عالية الأداء ، تم استخدام الخوارزميات والنماذج الرياضية لحل المشكلات في العلوم البيولوجية - من دراسة تعقيد الجينوم البشري إلى نمذجة سلوك الجزيئات الحيوية. تُستخدم الأساليب الحسابية بانتظام اليوم لتحليل واستخراج المعلومات المهمة من التجارب البيولوجية ، وكذلك للتنبؤ بسلوك الكائنات والأنظمة البيولوجية. في الواقع ، 10 من أصل 25 ورقة علمية استشهد بها تتناول الخوارزميات الحسابية المستخدمة في علم الأحياء [انظر ص. هنا ]، بما في ذلك النمذجة الكم [ هنا ، هنا ، هنا و هنا ]، تسلسل المحاذاة [ هنا ، هنا وهنا ] ، علم الوراثة الحسابي [انظر. هنا ] وانحراف الأشعة السينية في معالجة البيانات [راجع. هنا أن و هنا ].
على الرغم من هذا التقدم ، تظل العديد من المشكلات في علم الأحياء غير قابلة للحل من وجهة نظر حلها باستخدام التقنيات الحسابية الحالية. تتطلب أفضل الخوارزميات لمهام مثل توقع طي البروتين ، أو حساب تقارب الارتباط ليجند بجزيء كبير ، أو العثور على المحاذاة الجينية المثلى واسعة النطاق موارد حسابية تتجاوز حتى أقوى أجهزة الكمبيوتر الفائقة المتاحة اليوم.
قد يكمن حل هذه المشكلات في نقلة نوعية في تكنولوجيا الحوسبة. في الثمانينيات بشكل مستقل ، ريتشارد فاينمان [انظر. هنا ] ويوري مانين [انظر. هنا ] اقترح استخدام تأثيرات ميكانيكا الكم لإنشاء جيل جديد أكثر قوة من أجهزة الكمبيوتر.
أثبتت نظرية الكم أنها وصف ناجح للغاية للواقع المادي وأدت ، منذ إنشائها في أوائل القرن العشرين ، إلى تطورات مثل الليزر ، والترانزستورات ، والمعالجات الدقيقة لأشباه الموصلات. يستخدم الكمبيوتر الكمومي أكثر الخوارزميات كفاءة ، باستخدام عمليات غير ممكنة في الآلات الكلاسيكية. لا تعمل المعالجات الكمومية أسرع من أجهزة الكمبيوتر التقليدية ، لكنها تعمل بطريقة مختلفة تمامًا ، وتحقق تسريعًا غير مسبوق ، وتجنب العمليات الحسابية غير الضرورية. على سبيل المثال ، من المتوقع أن يستغرق حساب دالة الموجة الإلكترونية الإجمالية لجزيء الدواء المتوسط على أي كمبيوتر عملاق حديث باستخدام الخوارزميات التقليدية وقتًا أطول من عمر الكون الكامل [انظر المرجع. هنا] ، بينما حتى الكمبيوتر الكمي الصغير يمكنه حل هذه المشكلة في غضون أيام قليلة. بتشجيع من هذا الوعد بالميزة الكمية ، يواصل المهندسون والعلماء سعيهم للحصول على معالج كمي. ومع ذلك ، فإن الصعوبات التقنية في تصنيع وإدارة وحماية الأنظمة الكمية معقدة بشكل لا يصدق ، وقد ظهرت النماذج الأولية الأولى فقط في العقد الماضي.
من المهم أن نلاحظ أن المشاكل التقنية لبناء الحواسيب الكمومية لم توقف تطوير خوارزميات الحوسبة الكمومية. حتى في حالة عدم وجود أجهزة ، يمكن تحليل الخوارزميات رياضيًا ، وقد أتاح ظهور محاكيات الكمبيوتر الكمومية عالية الأداء وكذلك النماذج الأولية المبكرة في السنوات القليلة الماضية مزيدًا من البحث.
أظهر العديد من هذه الخوارزميات بالفعل تطبيقات محتملة واعدة في علم الأحياء. على سبيل المثال ، تسمح خوارزمية لتقدير المرحلة الكمومية بحساب قيم eigenvalues بشكل أسرع [انظر. هنا ] ، والتي يمكن استخدامها لفهم الارتباط الواسع النطاق بين أجزاء من البروتين أو لتحديد مركزية الرسم البياني في الشبكة البيولوجية. خوارزمية Harrow-Hasidim-Lloyd (HHL) الكمومية [cf. هنا ] يمكن حل بعض الأنظمة الخطية بشكل أسرع من أي خوارزمية كلاسيكية معروفة ، ويمكن أيضًا تطبيق طرق التعلم الإحصائي مع عملية تكيف أسرع بكثير والقدرة على إدارة كميات كبيرة من البيانات.
تمتلك خوارزميات التحسين الكمي مجالًا واسعًا للتطبيق في مجال طي البروتين واختيار المطابقة ، وكذلك في المشكلات المرتبطة بإيجاد الحدود الدنيا أو القصوى [انظر. هنا ]. أخيرًا ، تم تطوير التكنولوجيا مؤخرًا لمحاكاة الأنظمة الكمية التي تعد ، على سبيل المثال ، بإنتاج تنبؤات دقيقة لتفاعلات مستقبلات الأدوية [انظر المرجع. هنا ] أو للمشاركة في دراسة وفهم العمليات المعقدة والآليات الكيميائية مثل التمثيل الضوئي [انظر. هنا ]. يمكن للحوسبة الكمومية أن تغير بشكل كبير أساليب البيولوجيا نفسها ، كما فعلت الحوسبة الكلاسيكية في وقتها.
الادعاءات الأخيرة بشأن التفوق الكمي من Google [راجع. هنا] ، على الرغم من المتنازع عليها من قبل شركة IBM [cf. هنا ] ، تشير إلى أن عصر الحوسبة الكمومية ليس بعيدًا. من المتوقع أن تكون المعالجات الأولى التي تستخدم التأثيرات الكمية لإجراء عمليات حسابية مستحيلة لتكنولوجيا الكمبيوتر الكلاسيكية خلال العقد القادم [راجع. هنا ].
في هذا الاستعراض ، سنقوم بتفصيل النقاط الرئيسية التي تبشر فيها الحوسبة الكمومية بالبيولوجيا الحاسوبية. تحلل هذه المراجعات التأثير المحتمل للحوسبة الكمية في مجموعة متنوعة من المجالات ، بما في ذلك التعلم الآلي [cf. هنا ، هنا و هنا ]، الكم الكيمياء [راجع هنا ، هنا و هنا ] والتوليف المخدرات [انظر.هنا ]. كما نُشر مؤخرًا تقرير ورشة عمل NIMH حول الحوسبة الكمية في علوم الحياة [انظر ص. هنا ].
في هذه المراجعة ، نقدم أولاً وصفًا موجزًا لما تعنيه الحوسبة الكمومية ومقدمة قصيرة لمبادئ معالجة المعلومات الكمية. ثم نناقش ثلاثة مجالات رئيسية لعلم الأحياء الحسابي ، حيث أظهرت الحوسبة الكمومية تطورات خوارزمية واعدة: الأساليب الإحصائية وحسابات البنية الإلكترونية والتحسين. سيتم ترك بعض الموضوعات المهمة جانبًا ، على سبيل المثال ، خوارزميات السلسلة التي يمكن أن تؤثر على تحليل التسلسل [انظر. هنا ] ، خوارزميات التصوير الطبي [انظر. هنا ] ، الخوارزميات العددية للمعادلات التفاضلية [هنا ] ومشكلات رياضية أخرى أو طرق لتحليل الشبكات البيولوجية [ هنا ]. أخيرًا ، نناقش التأثير المحتمل للحوسبة الكمية على البيولوجيا الحسابية على المدى المتوسط إلى الطويل.
1. معالجة المعلومات الكمية
تعد أجهزة الكمبيوتر الكمومية بحل المشكلات في العلوم البيولوجية ، مثل التنبؤ بتفاعلات البروتينات الرابطة أو فهم التطور المشترك للأحماض الأمينية في البروتينات. وليس من السهل حلها ، ولكن القيام بذلك بشكل أسرع مما تتخيله مع أي جهاز كمبيوتر حديث. ومع ذلك ، فإن هذا التحول في النموذج يتطلب تغييرًا جوهريًا في تفكيرنا: أجهزة الكمبيوتر الكمومية مختلفة تمامًا عن سابقاتها الكلاسيكية. غالبًا ما تكون الظواهر الفيزيائية التي تكمن وراء الميزة الكمومية غير منطقية ومضادة للحدس ، واستخدام معالج كمي يتطلب تغييرًا أساسيًا في فهمنا للبرمجة. في هذا القسم ، نقدم مبادئ المعلومات الكمية وكيفية معالجتها لإجراء الحسابات.
نشرح كيف تعمل المعلومات بشكل مختلف في النظام الكمي ، حيث يتم تخزينها في كيوبتات ، وكيف يمكن معالجة هذه المعلومات باستخدام البوابات الكمومية. مثل المتغيرات والوظائف في لغة البرمجة ، تحدد الكيوبتات والبوابات الكمومية العناصر الأساسية لأي خوارزمية. سنقوم أيضًا بفحص سبب صعوبة إنشاء كمبيوتر كمي تقنيًا وما يمكن تحقيقه بمساعدة النماذج الأولية المتوقعة في السنوات القادمة. ستغطي هذه المقدمة النقاط الرئيسية فقط ؛ للحصول على دراسة شاملة اقرأ كتاب نيلسن وتشوانغ [ هنا ].
1.1. عناصر الخوارزميات الكمومية
1.1.1. معلومات الكم: مقدمة للكيوبت
المشكلة الأولى في تمثيل الحوسبة الكمومية هي فهم كيفية معالجة المعلومات. في المعالج الكمي ، تُخزَّن المعلومات عادةً في كيوبتات ، وهي التناظرية الكمومية للبتات الكلاسيكية. الكيوبت هو نظام فيزيائي ، مثل أيون ، محدد بمجال مغناطيسي [انظر. هنا ] أو فوتون مستقطب [انظر. هنا ] ، ولكن غالبًا ما يتم الحديث عنها بشكل مجردة. مثل قطة شرودنغر ، لا يمكن للكيوبت أن يأخذ الحالات 0 أو 1 فقط ، ولكن أيضًا أي مجموعة ممكنة من كلتا الحالتين. عندما يتم ملاحظة الكيوبت بشكل مباشر ، فإنه لن يكون في حالة تراكب ينهار إلى إحدى الحالات الممكنة ، تمامًا مثل قط شرودنجر ميتًا أو حيًا بعد فتح الصندوق [انظر. هنا]. والأهم من ذلك ، عندما يتم الجمع بين عدة كيوبتات ، يمكن أن تترابط ، والتفاعلات مع أي منها لها عواقب على الحالة الجماعية بأكملها. تُعد ظاهرة الارتباط بين الكيوبتات المتعددة ، والمعروفة باسم التشابك الكمومي ، موردًا أساسيًا للحوسبة الكمية.
في المعلومات الكلاسيكية ، تكون الوحدة الأساسية للمعلومات هي بت ، نظام به حالتان يمكن التعرف عليهما ، غالبًا ما يُشار إليهما 0 و 1. التناظرية الكمومية ، الكيوبت ، هي نظام من حالتين ، حالتيهما تسمى | 0⟩ و | 1⟩. نستخدم ترميز ديراك ، حيث يعرّف | *⟩ الحالة الكمومية. يتمثل الاختلاف الرئيسي بين المعلومات الكلاسيكية والكمية في أن الكيوبت يمكن أن يكون في أي تراكب للحالات | 0⟩ و | 1⟩:
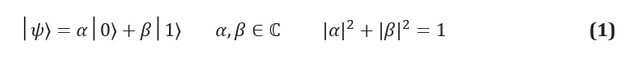
تُعرف المعاملات المعقدة α و باسم اتساع الحالات ، وهي مرتبطة بمفهوم رئيسي آخر في ميكانيكا الكم: تأثير البعد المادي. نظرًا لأن الكيوبتات عبارة عن أنظمة مادية ، يمكنك دائمًا وضع بروتوكول لقياس حالتها. على سبيل المثال ، إذا كانت الحالتان | 0⟩ و | 1⟩ تتطابقان مع حالات دوران الإلكترون في مجال مغناطيسي ، فإن قياس حالة الكيوبت هو ببساطة قياس طاقة النظام. تملي افتراضات ميكانيكا الكم أنه إذا كان النظام في حالة تراكب لنتائج القياس المحتملة ، فيجب أن يغير فعل القياس الحالة نفسها. سوف ينهار نظام التراكب في مرحلة القياس ؛ وبالتالي فإن القياس يدمر المعلومات التي يحملها الاتساع في الكيوبت.
تنشأ تداعيات حسابية مهمة عندما نفكر في أنظمة ذات كيوبتات متعددة يمكنها تجربة التشابك الكمي. التشابك هو ظاهرة ترتبط فيها مجموعة من الكيوبتات ، وأي عملية على إحدى هذه الكيوبتات ستؤثر على الحالة العامة لكل منهم. مثال قانوني على التشابك الكمي هو مفارقة أينشتاين - بودولسكي - روزين ، المقدمة في عام 1935 [راجع. هنا ]. ضع في اعتبارك نظامًا مكونًا من اثنين من الكيوبتات ، حيث يمكن أن يأخذ النظام المركب أي تراكب للحالات ، نظرًا لأن كل من الكيوبتات الفردية يمكن أن تأخذ أي تراكب للحالات {| 0⟩ و | 1⟩}. {| 00⟩، | 01⟩، | 10⟩، | 11 ⟩} (وبناءً عليه ، يمكن لنظام N-qubits أن يأخذ أيًا منسلاسل ثنائية ، من {| 0 ... 0⟩ إلى | 1 ... 1⟩}. إحدى حالات التراكب المحتملة للنظام هي ما يسمى بحالات بيل ، والتي تحتوي إحداها على الشكل التالي: إذا أخذنا قياسًا على أول كيوبت ، فيمكننا فقط ملاحظة | 0⟩ أو | 1⟩ ، ولكل منها احتمال 1/2. لا يؤدي هذا إلى إجراء أي تغييرات لحالة كيوبت واحدة. إذا كانت نتيجة أول كيوبت هي | 0⟩ ، فإن النظام سينهار إلى النظام | 01⟩ ، وبالتالي فإن أي قياس على الكيوبت الثاني سيعطي | 1⟩ مع احتمال 1 ؛ وبالمثل ، إذا كان القياس الأول | 1⟩ ، فإن القياس بالكيوبت الثاني سيعطي | 0⟩. تؤثر العملية (في هذه الحالة ، القياس بالنتيجة "0") المطبقة على الكيوبت الأول على النتائج التي يمكن رؤيتها عند قياس الكيوبت الثاني لاحقًا.

يعد وجود التشابك أمرًا أساسيًا للحوسبة الكمية المفيدة. لقد ثبت أن أي خوارزمية كمومية لا تستخدم التشابك يمكن تطبيقها على جهاز كمبيوتر كلاسيكي دون اختلاف كبير في السرعة [راجع. هنا أن و هنا ]. بشكل بديهي ، السبب هو مقدار المعلومات التي يمكن للحاسوب الكمومي معالجتها. إذا لم يكن نظام N qubit متشابكًا ، إذنيمكن وصف اتساع حالتها من خلال اتساع كل حالة بتة واحدة ، أي سعة 2N. ومع ذلك ، إذا كان النظام متشابكًا ، فستكون جميع السعات مستقلة ، وسيتشكل سجل كيوبتناقلات الأبعاد. تعد قدرة أجهزة الكمبيوتر الكمومية على معالجة كميات هائلة من المعلومات من خلال عمليات متعددة إحدى المزايا الرئيسية للخوارزميات الكمومية وتدعم قدرتها على حل المشكلات بشكل أسرع من تقنية الكمبيوتر التقليدية.
1.1.2. بوابات الكم
تتم معالجة المعلومات المخزنة في الكيوبتات باستخدام عمليات خاصة تُعرف بالبوابات الكمومية. البوابات الكمومية هي عمليات فيزيائية ، مثل نبضة ليزر موجهة إلى أيون كيوبت ، أو مجموعة من المرايا ومقسمات الحزمة التي يجب أن ينتقل الفوتون الكيوبت خلالها. ومع ذلك ، غالبًا ما يُنظر إلى البوابات على أنها عمليات مجردة. تفرض افتراضات ميكانيكا الكم بعض الشروط الصارمة على طبيعة البوابات الكمومية في الأنظمة المغلقة ، مما يسمح بتمثيلها في شكل مصفوفات وحدوية ، وهي عمليات خطية تحافظ على تطبيع النظام الكمي.
على وجه الخصوص ، فإن البوابة الكمية المطبقة على سجل متشابك لـ N كيوبت تكافئ مضاعفة المصفوفة × على متجه الإدخال ... إن قدرة الكمبيوتر الكمي على تخزين وإجراء عمليات حسابية لكميات هائلة من المعلومات هي في حدود- من خلال التلاعب بالعديد من العناصر - من الترتيب N - تشكل أساس قدرتها على توفير ميزة أسية محتملة على أجهزة الكمبيوتر الكلاسيكية.
في الأساس ، تعتبر البوابات الكمومية أي عملية مسموح بها في نظام كيوبت. تفرض افتراضات ميكانيكا الكم قيدين صارمين على شكل البوابات الكمومية. العوامل الكمومية خطية. الخطية هي حالة رياضية لها مع ذلك آثار عميقة على فيزياء الأنظمة الكمومية ، وبالتالي ، كيف يمكن استخدامها للحساب. إذا تم تطبيق المعامل الخطي على تراكب الحالات، والنتيجة هي تراكب الدول الفردية التي تتأثر بالمشغل. في الكيوبت ، هذا يعني: يمكن تمثيل العوامل الخطية كمصفوفات ، وهي ببساطة جداول تشير إلى تأثير عامل تشغيل خطي على كل حالة أساس. يوضح الشكل 1 (ج ، د) تمثيل مصفوفة بواحد من اثنين كيوبت وبوابتين من بت واحد. ومع ذلك ، لا تمثل كل مصفوفة بوابات كمية حقيقية. نتوقع أن تعطي البوابات الكمومية المطبقة على مجموعة من الكيوبتات مجموعة حقيقية مختلفة من الكيوبتات ، على وجه الخصوص ، مجموعة قياسية (على سبيل المثال ، في المعادلة (3) نتوقع أن
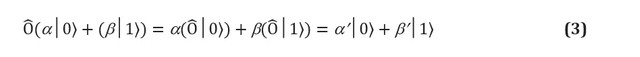
). يتم استيفاء هذا الشرط فقط إذا كانت المصفوفة التي تمثل البوابات الكمومية وحدوية ، أي U † U = UU † = I ، حيث U † هي المصفوفة U التي تم فيها إعادة ترتيب الصفوف والأعمدة ، وكان كل رقم مركب مترافق (أي يكتسب كل عنصر وهمي عاملًا سلبيًا). المصفوفة الوحدوية التعسفية × هي بوابة كمية N-qubit صالحة تمامًا.
في الحساب الكلاسيكي ، توجد بوابة واحدة غير تافهة للبتة الواحدة: البوابة NOT ، والتي تحول 0 إلى 1 والعكس صحيح. في الحوسبة الكمومية ، يوجد عدد لا حصر له من المصفوفات الوحدوية 2 × 2 ، وأي منها عبارة عن بوابة كمومية محتملة من واحد كيوبت. كان أحد النجاحات الأولى للحوسبة الكمومية هو اكتشاف أن هذه المجموعة الواسعة من الاحتمالات يمكن تحقيقها من خلال مجموعة من البوابات العالمية التي تؤثر على واحد أو اثنين من البتات الكمومية [انظر المرجع. هنا]. بعبارة أخرى ، بالنظر إلى البوابات الكمومية التعسفية ، هناك دائرة بوابات واحدة واثنين كيوبت يمكنها دفعها بدقة عشوائية. لسوء الحظ ، هذا لا يعني أن التقريب فعال. لا يمكن تقريب معظم البوابات الكمية إلا من خلال عدد أسي من البوابات من مجموعتنا العالمية. حتى لو كان من الممكن استخدام هذه البوابات لحل المشكلات المفيدة ، فإن تنفيذها سيستغرق وقتًا كبيرًا بشكل كبير ويمكن أن ينفي أي ميزة كمية. الشكل 1 (أ) مقارنة بت تقليدي مع بت كمي أو "كيوبت". بينما يمكن أن تأخذ البتة الكلاسيكية حالة واحدة فقط من حالتين ، 0 أو 1 ، يمكن أن تأخذ البتة الكمية أي حالة من الشكل

... غالبًا ما تُصوَّر الكيوبتات المفردة باستخدام تمثيل كرة بلوخ ، حيث يُفهم θ و على أنهما زاويتان سمتيتان وقطبيتان في مجال نصف قطر الوحدة. (ب) تخطيطي لمصيدة أيون كيوبت ، وهو أحد أكثر الأساليب شيوعًا للحوسبة الكمومية التجريبية. أيون (غالبًا) في فراغ عالي بواسطة المجالات الكهرومغناطيسية ومعرض لمجال مغناطيسي قوي. يتم فصل المستويات فائقة الدقة وفقًا لتأثير زيمان ، ويتم تحديد المستويين المحددين كحالتين | 0⟩ و | 1⟩. يتم تنفيذ البوابات الكمومية بواسطة نبضات ليزر مناسبة ، غالبًا ما تتضمن مستويات إلكترونية أخرى. تم اقتباس هذا الرسم البياني من [see. هنا ]. (ج) رسم تخطيطي لدائرة كمومية تنفذ X أو مقدار النفي المتحكم فيه (CNOT).
يظهر التمثيل والتغيير في مجال بلوخ. (د) الدائرة الكمية لتوليد حالة الجرسباستخدام بوابة Hadamard وبوابة CNOT (النفي المتحكم به). يشير الخط المنقط في منتصف المخطط التفصيلي إلى الحالة بعد تطبيق صمام Hadamard.
1.2 أجهزة الكم
لا تستطيع الخوارزميات الكمومية حل المشكلات المثيرة إلا إذا كانت تعمل على الأجهزة الكمومية المناسبة. هناك العديد من المقترحات المتنافسة لإنشاء معالج كمي قائم على الأيونات المحاصرة [انظر. هنا ] ، الدوائر فائقة التوصيل [انظر. هنا ] والأجهزة الضوئية [انظر. هنا]. ومع ذلك ، فإنهم جميعًا يواجهون مشكلة شائعة: أخطاء حسابية يمكن أن تدمر العملية الحسابية حرفيًا. أحد الركائز الأساسية للحوسبة الكمومية هو اكتشاف إمكانية القضاء على هذه الأخطاء باستخدام أكواد تصحيح الأخطاء الكمومية. لسوء الحظ ، تتطلب هذه الرموز أيضًا زيادة كبيرة جدًا في عدد الكيوبتات ، لذلك هناك حاجة إلى تحسينات فنية كبيرة لتحقيق التسامح مع الخطأ.
هناك العديد من مصادر الخطأ التي يمكن أن تؤثر على المعالج الكمي. على سبيل المثال ، يمكن أن يؤدي اتصال كيوبت مع بيئته إلى انهيار النظام في إحدى حالاته الكلاسيكية - وهي عملية تُعرف باسم فك الترابط.... يمكن للتقلبات الصغيرة أن تحول البوابات الكمية ، الأمر الذي سيؤدي في النهاية إلى نتائج مختلفة عما كان متوقعًا. تم تسجيل أقل البوابات عرضة للخطأ حتى الآن في معالج أيوني محاصر ، بمعدل خطأ واحد لكل منهماالبوابات و qubit واحدة وبنسبة خطأ 0.1٪ للبوابات يومين و qubit [ هنا و هنا ]. للمقارنة ، أفاد عمل حديث لـ Google عن دقة بنسبة 0.1٪ للبوابات أحادية الكيوبت و 0.3٪ لبوابتين كيوبت في معالج فائق التوصيل [انظر المرجع. هنا ]. بالنظر إلى أن فشل بوابة واحدة يمكن أن يفسد الحساب ، فمن السهل أن نرى أن انتشار الخطأ يمكن أن يجعل الحساب بلا معنى بعد سلسلة صغيرة من العناصر.
أحد الاتجاهات الرئيسية للحوسبة الكمومية هو تطوير أكواد تصحيح الأخطاء الكمومية. في التسعينيات ، أثبتت عدة مجموعات بحثية أن هذه الرموز يمكن أن تحقق حسابات تتسامح مع الأخطاء ، بشرط أن تكون معدلات خطأ البوابة أقل من عتبة معينة ، والتي تعتمد على الكود [انظر. هنا ، هنا ، هنا و هنا ]. من أكثر الطرق شيوعًا ، الكود السطحي ، يمكن أن تعمل بمعدلات خطأ تقترب من 1٪ [انظر المرجع. هنا ].
لسوء الحظ ، تتطلب أكواد تصحيح الخطأ الكمومي عددًا كبيرًا من الكيوبتات الفيزيائية الحقيقية لتشفير الكيوبت المنطقي المجرد المستخدم في الحساب ، ويزيد هذا الحمل مع معدل الخطأ. على سبيل المثال ، خوارزمية كمومية لتحليل الأعداد الأولية [انظر. هنا ] يمكن أن تتحلل بهدوء رقم 2000 بت باستخدام حوالي 4000 كيوبت ، وعند 16 جيجا هرتز ، ستستغرق هذه العملية حوالي يوم واحد من العمل. بافتراض أن معدل الخطأ هو 0.1٪ ، فإن نفس الخوارزمية ، باستخدام كود السطح لتصحيح أخطاء البيئة ، ستستغرق عدة ملايين من البتات ونفس القدر من الوقت [see. هنا]. بالنظر إلى أن السجل الحالي للمعالج الكمي المتحكم فيه والقابل للبرمجة هو 53 كيوبت [انظر. هنا ] ، لا يزال هناك طريق طويل لنقطعه في اتجاه البحث هذا.
بذلت العديد من المجموعات جهودًا لتطوير خوارزميات يمكن تشغيلها على ما يسمى بمعالجات الضوضاء الكمومية متوسطة الحجم [cf. هنا ]. على سبيل المثال ، تجمع الخوارزميات المتغيرة بين جهاز كمبيوتر كلاسيكي ومعالج كمي صغير ، وتؤدي قدرًا كبيرًا من الحسابات الكمومية القصيرة التي يمكن إنجازها قبل أن تصبح الضوضاء كبيرة.
غالبًا ما تستخدم هذه الخوارزميات دائرة كمية ذات معلمات ، والتي تؤدي مهمة صعبة بشكل خاص ، وتستخدم جهاز كمبيوتر كلاسيكي لتحسين المعلمات. طريقة الدقة هي منطقة للحد من الخطأ ، وبدلاً من تحقيق التسامح مع الخطأ ، تم إجراء محاولة لتقليل الأخطاء بأقل جهد ممكن لدفع دوائر بوابة أكبر. هناك عدد من الأساليب التي تتضمن استخدام عمليات إضافية لتجاهل عمليات التشغيل التي بها أخطاء [راجع. هنا ] أو التلاعب في معدل الخطأ لاستقراء النتيجة الصحيحة [راجع. هنا و هنا]. على الرغم من أن التطبيقات الرئيسية ستتطلب حواسيب كمومية كبيرة جدًا تتحمل الأخطاء ؛ من المتوقع أن تحل الأجهزة المتوفرة خلال العقد القادم هذه المشكلات [انظر هنا ].
2. الأساليب الإحصائية والتعلم الآلي
في علم الأحياء الحسابي ، حيث غالبًا ما يكون الهدف هو جمع كميات هائلة من البيانات ، تعد الأساليب الإحصائية والتعلم الآلي تقنيات أساسية. على سبيل المثال ، في علم الجينوم ، تُستخدم نماذج ماركوف المخفية (HMM) على نطاق واسع للتعليق على المعلومات حول الجينات [انظر. هنا ] ؛ في اكتشاف الأدوية ، تم تطوير مجموعة واسعة من النماذج الإحصائية لتقييم الخصائص الجزيئية أو للتنبؤ بربط بروتين يجند [انظر. هنا ] ؛ وفي علم الأحياء البنيوي ، تم استخدام الشبكات العصبية العميقة للتنبؤ بوصلات البروتين [انظر. هنا ] والبنية الثانوية [انظر. هنا ] ، ومؤخرًا أيضًا هياكل بروتينية ثلاثية الأبعاد [انظر. هنا ].
غالبًا ما يكون تدريب وتطوير هذه النماذج مكثفًا من الناحية الحسابية. كان أحد العوامل المحفزة للتطورات الحديثة في التعلم الآلي هو إدراك أن وحدات معالجة الرسومات للأغراض العامة (GPU) يمكنها تسريع التعلم بشكل كبير. من خلال توفير خوارزميات أسرع بشكل مضاعف للتعلم الآلي ، يمكن لنماذج الحوسبة الكمومية أن توفر اهتمامًا مماثلًا بتركيز التطبيق على المشكلات العلمية.
في هذا القسم ، سنشرح كيف يمكن للحوسبة الكمومية تسريع العديد من طرق التعلم الإحصائي.
2.1. مزايا وعيوب التعلم الآلي الكمي
ننظر أولاً إلى الفوائد التي يوفرها الكمبيوتر الكمومي للتعلم الآلي. باستثناء الأمثلة المثالية ، لا يمكن لأجهزة الكمبيوتر الكمومية أن تتعلم معلومات أكثر من الكمبيوتر التقليدي [cf. هنا ]. ومع ذلك ، من حيث المبدأ ، يمكن أن تكون أسرع بكثير وقادرة على معالجة بيانات أكثر بكثير من نظيراتها الكلاسيكية. على سبيل المثال ، يحتوي الجينوم البشري على 3 مليارات زوج أساسي ، والتي يمكن تخزينها في 1.2 ×بتات كلاسيكية - حوالي 1.5 غيغابايت. يتضمن سجل N كيوبتالسعات ، كل منها يمكن أن يمثل بتة كلاسيكية عن طريق ضبط السعة k إلى 0 أو 1 مع عامل التطبيع المناسب. وبالتالي ، يمكن تخزين الجينوم البشري في 34 كيوبت تقريبًا. في حين أن هذه المعلومات لا يمكن استخلاصها من الكمبيوتر الكمومي ، إلا أنه حتى يتم إعداد حالة معينة ، يمكن تنفيذ خوارزميات معينة للتعلم الآلي عليها. والأهم من ذلك ، أن مضاعفة حجم السجل إلى 68 كيوبت يترك مساحة كافية لتخزين الجينوم الكامل لكل شخص على قيد الحياة في العالم. سيكون عرض وتحليل مثل هذه الكميات الضخمة من البيانات متسقًا تمامًا مع قدرات حتى كمبيوتر كمي صغير يتحمل الأخطاء.
يمكن أيضًا أن تكون عمليات معالجة هذه المعلومات أسرع بشكل كبير. على سبيل المثال ، تقتصر خوارزميات التعلم الآلي المتعددة على الانعكاس طويل المدى لمصفوفة التغاير مع عقوبةعلى أبعاد المصفوفة. ومع ذلك ، فإن الخوارزمية التي اقترحها Harrow و Hassidim و Lloyd [cf. هنا ] ، يسمح لك بقلب المصفوفة إلىفي ظل بعض الظروف. تتمثل الفكرة الرئيسية في أنه ، على عكس وحدات معالجة الرسومات ، التي تسرع العمليات الحسابية من خلال التوازي الهائل ، تتمتع الخوارزميات الكمومية بميزة تعقيد الخوارزميات الحسابية المستخدمة مباشرة. في بعض الحالات ، خاصة مع التسارع الأسي الحالي ، يمكن لأجهزة الكمبيوتر الكمومية متوسطة الحجم حل مشاكل التعلم المتاحة فقط لأكبر أجهزة الكمبيوتر العملاقة الكلاسيكية المتاحة اليوم.
تحسين تخزين البيانات ومعالجتها له فوائد ثانوية. تتمثل إحدى نقاط القوة في الشبكات العصبية في قدرتها على إيجاد تمثيلات موجزة للبيانات [انظر. هنا]. نظرًا لأن المعلومات الكمومية أكثر عمومية من المعلومات الكلاسيكية (بعد كل شيء ، تنقسم حالات البت الكلاسيكي إلى eigenstates | 0⟩ و | 1⟩ ، أو qubit) ، فمن الممكن تمامًا أن تتمكن نماذج التعلم الآلي الكمي من استيعاب المعلومات بشكل أفضل من النماذج الكلاسيكية ... من ناحية أخرى ، تعمل الخوارزميات الكمومية ذات التعقيد الزمني اللوغاريتمي أيضًا على تحسين سرية البيانات [انظر. هنا ]. منذ التدريب يتطلب النموذجو و يتطلب إعادة بناء المصفوفة ، بالنسبة لمجموعة بيانات كبيرة بما يكفي ، من المستحيل استعادة جزء كبير من المعلومات ، على الرغم من أن التدريب الفعال للنموذج لا يزال ممكنًا. في سياق البحث الطبي الحيوي ، يمكن أن يسهل ذلك تبادل البيانات مع ضمان السرية.
لسوء الحظ ، على الرغم من أن خوارزميات التعلم الآلي الكمومية على الورق يمكن أن تتفوق إلى حد كبير على نظيراتها الكلاسيكية ، لا تزال هناك صعوبات عملية. غالبًا ما تكون الخوارزميات الكمية عبارة عن إجراءات فرعية تحول المدخلات إلى مخرجات. تظهر المشاكل على وجه التحديد في هاتين المرحلتين: كيفية إعداد المدخلات الكافية وكيفية استخراج المعلومات من المخرجات [انظر. هنا ]. لنفترض ، على سبيل المثال ، أننا نستخدم خوارزمية HHL [see. هنا ] لحل نظام خطي للشكل... في نهاية الروتين الفرعي ، ستخرج الخوارزمية سجل كيوبت في الحالة التالية: هنا
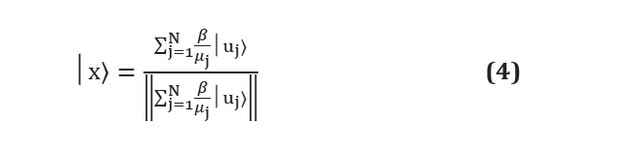
و هي المتجهات الذاتية والقيم الذاتية لـ A ، و - معامل j-th يتم التعبير عنها من حيث المتجهات الذاتية لـ A ، والمقام هو ببساطة ثابت تطبيع. يمكن ملاحظة أن هذا يتوافق مع المعاملات، والتي يتم تخزينها في اتساع حالات مختلفة مثل ولا يمكن الوصول إليها مباشرة. سيؤدي قياس سجل كيوبت إلى انهياره في إحدى حالات المتجه الذاتي ، وإعادة تقدير سعة كل منها القياسات المطلوبة ، والتي تفوق في المقام الأول أي ميزة للخوارزمية الكمومية.
HHL والعديد من الخوارزميات الأخرى مفيدة فقط لحساب الخاصية العامة للحل ، مثل القيمة المتوقعة. بمعنى آخر ، لا يمكن لـ HHL توفير حل لنظام المعادلات أو عكس المصفوفة في الوقت اللوغاريتمي ، إلا إذا كنا مهتمين فقط بالخصائص العامة للحل ، والتي يمكن الحصول عليها باستخدام عدة قياسات يمكن ملاحظتها فيزيائيًا. هذا يقيد استخدام بعض الإجراءات الفرعية ، ولكن هناك العديد من الاقتراحات للتغلب على هذه المشكلة.
يعد إدخال المعلومات في الكمبيوتر الكمومي مشكلة أكبر بكثير. تفترض معظم خوارزميات التعلم الآلي الكمومي أن الكمبيوتر الكمومي لديه حق الوصول إلى مجموعة البيانات في شكل حالة تراكب ؛ على سبيل المثال ، يوجد سجل كيوبت في حالة من الشكل: هنا - | bin (ي) هي حالة تعمل كمؤشر ، و

هي السعة المقابلة. يمكن استخدام هذا ، على سبيل المثال ، لتخزين عناصر متجه أو مصفوفة. من حيث المبدأ ، هناك دائرة كمية يمكنها تحضير هذه الحالة من خلال التصرف في حالة | 0 ... 0⟩ على سبيل المثال. ومع ذلك ، قد يكون تنفيذه صعبًا للغاية ، لأننا نتوقع أن التقريب لحالة كمية عشوائية سيكون صعبًا بشكل كبير وسيدمر أي ميزة كمية محتملة.
تفترض معظم الخوارزميات الكمومية الوصول إلى ذاكرة الوصول العشوائي الكمية (QRAM) [انظر. هنا ] ، وهو جهاز الصندوق الأسود القادر على بناء هذا التراكب. على الرغم من اقتراح بعض الرسومات [انظر. هنا و هنا] ، على حد علمنا ، لا يوجد جهاز يعمل حتى الآن. علاوة على ذلك ، حتى لو كان مثل هذا الجهاز متاحًا ، فليس هناك ما يضمن أنه لن يخلق اختناقات تفوق فوائد الخوارزمية الكمومية. على سبيل المثال ، اقتراح حديث قائم على مخطط لـ QRAM [cf. هنا ] يوضح التكلفة الخطية الحتمية لعدد الحالات التي تفوق أي خوارزمية زمنية لوغاريتمية. أخيرًا ، حتى إذا لم يقدم QRAM أي تكلفة إضافية ، فلا يزال يتعين إجراء المعالجة المسبقة الكلاسيكية - على سبيل المثال الجينوم ، سيكون الوصول إلى 12 إكسابايت من التخزين الكلاسيكي مطلوبًا.
أخيرًا ، يجب أن نؤكد أن خوارزميات التعلم الآلي الكمومي ليست خالية من واحدة من أكثر المشاكل شيوعًا في التطبيقات العملية: نقص البيانات ذات الصلة. يعد توفر كميات كبيرة من البيانات أمرًا بالغ الأهمية لنجاح العديد من التطبيقات العملية للذكاء الاصطناعي في العلوم الجزيئية ، مثل التطوير الجزيئي de novo [انظر المرجع. هنا ]. ومع ذلك ، يمكن أن تكون قوة الخوارزميات الكمومية مفيدة مثل التطورات العلمية والتكنولوجية مثل ظهور المختبرات ذاتية الإدارة [انظر المرجع. هنا ] توفير المزيد والمزيد من البيانات.
يمتلك التعلم الآلي الكمي القدرة على تغيير الطريقة التي نعالج بها البيانات البيولوجية ونحللها. ومع ذلك ، فإن التحديات العملية الحالية لتنفيذ تقنيات الكم لا تزال كبيرة.
2.2. خوارزميات التعلم الآلي الكمي
2.2.1. التعلم بدون معلم
يتضمن التعلم غير الخاضع للإشراف العديد من التقنيات لاستخراج المعلومات من مجموعات البيانات غير المميزة. في علم الأحياء ، حيث حفز تسلسل الجيل التالي والتعاون الدولي الكبير جمع البيانات ، وجدت هذه الأساليب استخدامًا واسع النطاق ، على سبيل المثال ، لتحديد العلاقات بين عائلات الجزيئات الحيوية [انظر. هنا ] أو الجينومات المشروحة [انظر. هنا ].
أحد أشهر خوارزميات التعلم غير الخاضعة للإشراف هو تحليل المكون الأساسي (PCA) ، والذي يحاول تقليل أبعاد البيانات من خلال إيجاد مجموعات خطية من الميزات التي تزيد من التباين [cf. هنا]. تُستخدم هذه الطريقة على نطاق واسع في جميع أنواع مجموعات البيانات عالية الأبعاد ، بما في ذلك بيانات المصفوفة الدقيقة للحمض النووي الريبي وبيانات قياس الطيف الكتلي [انظر. هنا ]. تم اقتراح خوارزمية كمومية لـ PCA من قبل مجموعة من الباحثين [see. هنا ]. بشكل أساسي ، تبني هذه الخوارزمية مصفوفة تغاير البيانات في الكمبيوتر الكمومي وتستخدم روتينًا فرعيًا يُعرف باسم تقدير المرحلة الكمومية لحساب المتجهات الذاتية في الوقت اللوغاريتمي. ناتج الخوارزمية هو حالة تراكب للشكل: هنا

هو المكون الرئيسي j-th ، و - القيمة الذاتية المقابلة. نظرًا لأن PCA مهتم بقيم eigenvalues الكبيرة ، والتي تعد المكونات الرئيسية للتباين ، فإن قياس الحالة النهائية سيعطي مكونًا رئيسيًا مناسبًا مع احتمال كبير. سيؤدي تكرار الخوارزمية عدة مرات إلى توفير مجموعة من المكونات الأساسية. هذا الإجراء قادر على تقليل أبعاد الكم الهائل من المعلومات التي يمكن تخزينها في الكمبيوتر الكمومي.
كما تم اقتراح خوارزمية كمومية لطريقة محددة لتحليل البيانات الطوبولوجية ، وبالتحديد للتماثل المستقر [انظر. هنا ]. يحاول تحليل البيانات الطوبولوجية استخراج المعلومات باستخدام الخصائص الطوبولوجية في هندسة مجموعات البيانات ؛ تم استخدامه ، على سبيل المثال ، في دراسة تجميع البيانات [انظر.هنا ] وتحليل الشبكة [انظر. هنا ]. لسوء الحظ ، فإن أفضل الخوارزميات الكلاسيكية لها اعتماد أسي في بُعد المشكلة ، مما يحد من تطبيقها. خوارزمية لويد وآخرون. يستخدم أيضًا روتينًا لتقدير الطور الكمومي لتسريع قطري المصفوفة بشكل كبير ، والوصول إلى التعقيد... يمكن أن يؤدي وجود خوارزمية فعالة لإجراء التحليل الطوبولوجي إلى تحفيز تطبيقها لتحليل المشكلات في العلوم البيولوجية.
2.2.2. التعلم تحت الإشراف
يشير التعلم الخاضع للإشراف إلى مجموعة من الأساليب التي يمكن استخدامها لعمل تنبؤات بناءً على البيانات المصنفة. الهدف هو بناء نموذج يمكنه تصنيف أو التنبؤ بخصائص الأمثلة غير المرئية. يستخدم التعلم الخاضع للإشراف على نطاق واسع في علم الأحياء لحل مشكلات متنوعة مثل التنبؤ بألفة ارتباط ليجند بالبروتين [انظر. هنا ] وتشخيص الأمراض باستخدام الكمبيوتر [انظر. هنا ]. دعونا نلقي نظرة على ثلاثة مناهج التعلم تحت الإشراف.
دعم شاحنات النقل(آلة متجه دعم اللغة الإنجليزية - SVM) هي خوارزمية تعلم الآلة التي تعثر على المستوى الفائق الأمثل الذي يفصل بين فئات البيانات. تم استخدام SVM على نطاق واسع في صناعة الأدوية لتصنيف بيانات الجزيئات الصغيرة [cf. هنا ]. اعتمادًا على النواة ، عادةً ما يأخذ تدريب SVM من قبل ... ريبينتروست [انظر. هنا ] قدمنا خوارزمية كمومية يمكنها تدريب SVM مع نواة متعددة الحدود، وبعد ذلك تم تمديده إلى جوهر وظيفة الأساس الشعاعي (RBF) [انظر. هنا ]. لسوء الحظ ، ليس من الواضح كيفية تنفيذ العمليات غير الخطية المستخدمة على نطاق واسع في SVM ، نظرًا لأن العمليات الكمية تقتصر على أن تكون خطية. من ناحية أخرى ، يسمح الكمبيوتر الكمومي بأنواع أخرى من النوى لا يمكن تحقيقها في الكمبيوتر الكلاسيكي [انظر. هنا ].
انحدار العملية الغاوسية (GP) هي تقنية شائعة الاستخدام لبناء نماذج بديلة ، على سبيل المثال في تحسين بايز [انظر. هنا ]. تُستخدم الممارسين العامين أيضًا على نطاق واسع لإنشاء نماذج كمية العلاقة بين الهيكل والنشاط (QSAR) لخصائص الأدوية.هنا ] ، ومؤخرا أيضًا لنمذجة الديناميات الجزيئية [انظر. هنا ]. إحدى عيوب انحدار GP هي القيمة العاليةانقلاب مصفوفة التغاير. تشاو وزملاؤه [انظر. هنا ] اقترح استخدام خوارزمية HHL للأنظمة الخطية لعكس هذه المصفوفة ، وتحقيق تسارع أسي (طالما أن المصفوفة متفرقة ومكيفة جيدًا) - وهي خاصية يتم تحقيقها غالبًا بواسطة مصفوفات التغاير. والأهم من ذلك ، تم توسيع هذه الخوارزمية لحساب لوغاريتم الاحتمال المحدد [راجع. هنا ] ، وهي خطوة مهمة لتحسين المعلمة الفائقة.
أحد أكثر الطرق شيوعًا في علم الأحياء الحسابي هو نموذج ماركوف المخفي (HMM) ، والذي يستخدم على نطاق واسع في شرح الجينات الحسابية ومحاذاة التسلسل [راجع. هنا]. تحتوي هذه الطريقة على عدد من الحالات المخفية ، كل منها مرتبطة بسلسلة ماركوف ؛ تؤدي الانتقالات بين الحالات المخفية إلى تغييرات في التوزيع الأساسي. في الأساس ، لا يمكن تنفيذ HMM بشكل مباشر في الكمبيوتر الكمومي: يتطلب أخذ العينات نوعًا من القياس الذي سيعطل النظام. ومع ذلك ، هناك صياغة من حيث الأنظمة الكمية المفتوحة ، أي نظام كمي على اتصال بالبيئة ، والذي يسمح لنظام ماركوف [انظر. هنا ]. على الرغم من عدم اقتراح أي تحسينات على خوارزمية Baum-Welch الكلاسيكية لتدريب HMMs ، فقد تم العثور على HMMs الكمومية لتكون أكثر تعبيرًا: يمكنها إعادة إنتاج توزيع مع حالات مخفية أقل [راجع هنا]. قد يؤدي هذا إلى تطبيق أوسع للطريقة في علم الأحياء الحسابي.
2.2.3. الشبكات العصبية والتعلم العميق
تم تحفيز التطورات الحديثة في التعلم الآلي من خلال اكتشاف أن طبقات متعددة من الشبكات العصبية الاصطناعية يمكنها اكتشاف الهياكل المعقدة في البيانات الأولية [انظر ص. هنا ]. بدأ التعلم العميق يتغلغل في كل تخصص علمي ، وفي علم الأحياء الحسابي ، تشمل تطوراته التنبؤ الدقيق للروابط البروتينية. هنا ] ، تحسين تشخيص بعض الأمراض [انظر. هنا ] ، التصميم الجزيئي [cf. هنا ] والنمذجة [انظر. هنا أن و هنا ].
نظرًا للتقدم الكبير في دراسة الشبكات العصبية ، تم القيام بعمل كبير لتطوير نظائر كمومية يمكنها دفع المزيد من التقدم في التكنولوجيا.
غالبًا ما يشير اسم الشبكة العصبية الاصطناعية إلى الإدراك متعدد الطبقات للشبكة العصبية ، حيث يأخذ كل خلية عصبية مزيجًا خطيًا مرجحًا من مدخلاته ويعيد النتيجة من خلال وظيفة تنشيط غير خطية. التحدي الرئيسي في تطوير التناظرية الكمومية هو كيفية تنفيذ وظيفة التنشيط غير الخطية باستخدام بوابات الكم الخطية. كان هناك الكثير من الاقتراحات مؤخرًا ، وتشمل بعض الأفكار القياسات [cf. هنا ، هنا و هنا ]، والبوابات الكم المبددة [ هنا] ، والحوسبة الكمومية ذات المتغير المستمر [ هنا ] وإدخال كيوبتات إضافية لبناء بوابات خطية تحاكي اللاخطية [انظر. هنا ]. تهدف هذه الأساليب إلى تنفيذ شبكة عصبية كمومية من المتوقع أن تكون أكثر تعبيراً من الشبكة العصبية الكلاسيكية بسبب القوة الأكبر للمعلومات الكمية. مزايا أو عيوب توسيع نطاق تدريب الإدراك متعدد الطبقات في الكمبيوتر الكمومي غير واضحة ، على الرغم من أن التركيز ينصب على التعبير المعزز المحتمل لهذه النماذج.
ركز قدر كبير من الجهود الأخيرة على آلات بولتزمان ، الشبكات العصبية المتكررة القادرة على العمل كنماذج توليد. بمجرد التدريب ، يمكنهم إنشاء أنماط جديدة مماثلة لمجموعة التدريب.
النماذج التوليدية لها تطبيقات مهمة ، على سبيل المثال ، في التصميم الجزيئي de novo [cf. هنا أن و هنا ]. على الرغم من أن آلات Boltzmann قوية للغاية ، إلا أنه من الضروري حل المشكلة المعقدة لأخذ العينات من توزيع Boltzmann من أجل حساب التدرجات وإجراء التدريب ، مما يحد من تطبيقها العملي. تم اقتراح خوارزميات الكم باستخدام آلة D-Wave [انظر. هنا ، هنا و هنا ] أو خوارزمية الدائرة [انظر.هنا ] ؛ هذه العينة من توزيع Boltzmann أسرع تربيعًا مما هو ممكن في الإصدار الكلاسيكي [انظر. هنا ].
في الآونة الأخيرة ، تم اقتراح دليل إرشادي للتدريب الفعال لآلات بولتزمان الكمومية ، بناءً على درجة حرارة النظام [انظر. هنا ]. علاوة على ذلك ، في بعض الأعمال ، تم اقتراح تطبيقات كمية لشبكات الخصومة التوليدية (GANs) [انظر. هنا ، هنا و هنا ]. تتضمن هذه التطورات تحسين النماذج التوليدية مع تطور أجهزة الحوسبة الكمية.
3. المحاكاة الفعالة لأنظمة الكم
وفقًا للنماذج ، يتم تنظيم الكيمياء عن طريق نقل الإلكترون. يتم التحكم أيضًا في التفاعلات الكيميائية ، وكذلك التفاعلات بين الكيانات الكيميائية ، عن طريق توزيع الإلكترونات وطبيعة الطاقة الحرة التي تشكلها. تتلخص مشكلات مثل توقع ارتباط الترابط بالبروتين أو فهم المسار التحفيزي للإنزيم في فهم البيئة الإلكترونية. لسوء الحظ ، فإن نمذجة هذه العمليات صعبة للغاية. الخوارزمية الأكثر فاعلية لحساب طاقة نظام من الإلكترونات ، تفاعل التكوين الكامل (FCI) ، والذي يتوسع بشكل كبير مع نمو عدد الإلكترونات ، وحتى الجزيئات التي تحتوي على عدة ذرات كربون بالكاد متاحة للبحث الحسابي [انظر. هنا]. على الرغم من وجود العديد من الأساليب التقريبية ، موصوفة بعمق وعلى نطاق واسع في المنشورات حول نظرية الكثافة الوظيفية [انظر. هنا و هنا ]، يمكن أن تكون غير دقيقة وحتى تفشل فجأة في كثير من الحالات المثيرة للاهتمام، مثل محاكاة لحالة استجابة عابرة [راجع هنا ]. من شأن خوارزمية دقيقة وفعالة لدراسة البنية الإلكترونية أن توفر فهمًا أفضل للعمليات البيولوجية وأيضًا تفتح الفرص لتطوير الجيل التالي من التفاعلات البيولوجية.
تم اقتراح أجهزة الكمبيوتر الكمومية في الأصل كطريقة لنمذجة أكثر كفاءة للأنظمة الكمية. في عام 1996 ، أوضح Seth Lloyd أن هذا ممكن لأنواع معينة من الأنظمة الكمية [ هنا] ، وبعد عقد من الزمان ، أظهر آلان أسبورو جوزيك وزملاؤه أن الأنظمة الكيميائية هي إحدى هذه الحالات [ هنا ]. على مدى العقدين الماضيين ، كان هناك بحث كبير في طرق النمذجة الدقيقة للأنظمة الكيميائية التي يمكنها حساب الخصائص التي تهم البحث.
3.1. مزايا وعيوب محاكاة الكم
من حيث المبدأ ، فإن الكمبيوتر الكمي قادر على حل مشكلة البنية الإلكترونية المترابطة بالكامل (معادلات FCI) بكفاءة ، والتي ستكون الخطوة الأولى لتقدير طاقات الربط بدقة ، وكذلك لمحاكاة ديناميكيات الأنظمة الكيميائية. ركزت الكيمياء الحسابية الكلاسيكية بشكل حصري تقريبًا على الطرق التقريبية ، والتي كانت مفيدة ، على سبيل المثال ، لتقدير الكميات الحرارية الكيميائية للجزيئات الصغيرة [ هنا] ، ولكن هذا قد لا يكون كافيا للعمليات المرتبطة بكسر أو تكوين الروابط. في المقابل ، يمكن للمعالجات الكمومية أن تحل مشكلة إلكترونية عن طريق مائل مباشرة مصفوفة FCI ، وإعطاء نتيجة دقيقة ضمن مجموعة أساس معينة وبالتالي حل العديد من المشاكل الناشئة عن الأوصاف غير الصحيحة لفيزياء العمليات الجزيئية (على سبيل المثال ، استقطاب الروابط) ... علاوة على ذلك ، على عكس الأساليب الكلاسيكية ، فإنها لا تتطلب بالضرورة عملية تكرارية ، على الرغم من أن الافتراض الأولي لا يزال مهمًا.
على الرغم من أن أجهزة الكمبيوتر الكمومية لم يتم دراستها بعمق ، إلا أنها تغلبت أيضًا على التقريبات المقيدة التي كانت مطلوبة في الحوسبة الكلاسيكية. على سبيل المثال ، تأخذ صياغة المحاكاة الكمومية في الفضاء الحقيقي تلقائيًا في الاعتبار وظيفة الموجة النووية في غياب تقريب بورن-أوبنهايمر [ هنا ]. يسمح هذا للفرد بدراسة التأثيرات غير الثابتة للحرارة لبعض الأنظمة المعروفة بأهميتها لطفرة الحمض النووي [انظر. هنا ] وآلية عمل العديد من الإنزيمات [ هنا ]. كما تم اقتراح تطبيقات الحوسبة الكمومية لنمذجة النظام النسبي [انظر. هنا ] ، وهي مفيدة لدراسة المعادن الانتقالية التي تظهر في المراكز النشطة للعديد من الإنزيمات.
في مقال بقلم ريشر وزملائه [انظر هنا ] تم الكشف عن مفهوم المقياس الزمني لحساب الهياكل الإلكترونية في الكمبيوتر الكمومي. اعتبر المؤلفون العامل المساعد FeMo من إنزيم النيتروجين ، آلية تثبيت النيتروجين التي لم يتم دراستها بعد وهي معقدة للغاية بحيث لا يمكن دراستها باستخدام الأساليب الحسابية الحديثة. سيستغرق الحد الأدنى لحساب خط الأساس FCI لـ FeMoCo عدة أشهر وحوالي 200 مليون كيوبت من أعلى فئة متاحة اليوم. ومع ذلك ، يجب أن تتغير هذه التقديرات مع التطور السريع للتكنولوجيا. على مدى 3 سنوات منذ النشر ، أدت التطورات الخوارزمية بالفعل إلى تقليل متطلبات الوقت بعدة أوامر من حيث الحجم [انظر. هنا]. بالإضافة إلى الأساليب الأكثر فاعلية للهيكل الإلكتروني ، هناك إصدارات سريعة من الأساليب التقريبية الحديثة التي تم التحقيق فيها مؤخرًا [cf. هنا و هنا ] يمكن تسريع كبيرة النماذج، والتي يمكن أن تكون مفيدة، على سبيل المثال، عند دراسة الإحداثيات من ردود الفعل من التفاعلات الإنزيمية، المنطقة التي هي مشكلة لالإنزيمات الحسابية [ هنا ]. علاوة على ذلك ، من خلال الفهم الأفضل للتفاعلات بين الجزيئات ، التي يتم تحفيزها من خلال الوصول إلى حسابات مترابطة تمامًا أو الوصول إلى نطاق ترددي أسرع يعمل على تحسين المعلمات ، يمكن للنمذجة الكمومية تحسين تقنيات النمذجة غير الكمية بشكل كبير مثل مجالات القوة.
نقطة أخيرة يجب البحث عنها هي أنه على عكس المجالات الأخرى لأبحاث الخوارزمية ، مثل التعلم باستخدام الآلات الكمومية ، هناك عدد من خوارزميات المحاكاة الكمومية قصيرة المدى التي يمكن تشغيلها على أجهزة موجودة مسبقًا غير متوقعة. أبلغت مجموعات تجريبية عديدة حول العالم عن عروض توضيحية ناجحة لهذه الخوارزميات [ هنا ، هنا ، هنا ، هنا ].
لسوء الحظ ، هناك أيضًا بعض العيوب في نمذجة الأنظمة الكمومية. كما نوقش أعلاه ، من الصعب للغاية استخراج المعلومات من الكمبيوتر الكمومي. إعادة بناء دالة الموجة بأكملها أصعب من حسابها بالطريقة الكلاسيكية. هذا عيب مهم للمشاكل الكيميائية ، حيث الحجج القائمة على البنية الإلكترونية هي المصدر الرئيسي للفهم. ومع ذلك ، بالمقارنة مع التعلم الآلي ، تفوق المزايا بكثير العيوب ، ومن المتوقع أن تكون المحاكاة الكمومية واحدة من أولى التطبيقات المفيدة للحوسبة الكمومية العملية [انظر المرجع. هنا ].
3.2 الحوسبة الكمومية المتسامحة مع الخطأ
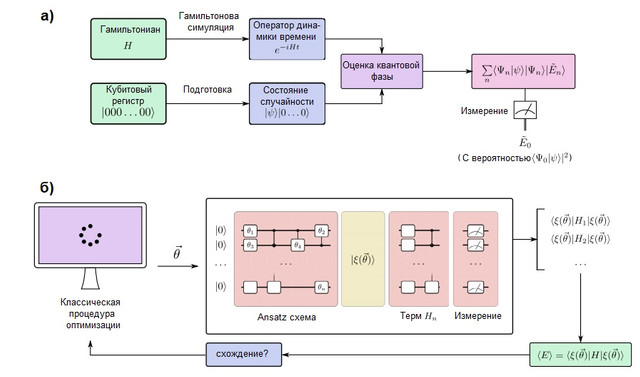
الشكل 2. (أ) خوارزمية محاكاة كمومية في كمبيوتر كمي متسامح مع الأخطاء. تنقسم الكيوبتات إلى سجلين: أحدهما مُعد في الحالة، والتي تشبه وظيفة الموجة المستهدفة ، بينما تظل الأخرى في الحالة ... تُستخدم خوارزمية تقدير الطور الكمومي (QPE) للعثور على القيم الذاتية لمشغل تطور الوقت، والتي تم إعدادها باستخدام طرق النمذجة الهاميلتونية. بعد QPE ، يعطي قياس الكمبيوتر الكمي طاقة الحالة الأرضية مع الاحتماللذلك من المهم تحضير حالة التخمين مع تداخل غير صفري مع دالة الموجة الحقيقية. (ب) خوارزمية محاكاة الكم المتغيرة في كمبيوتر كمي قصير المدى. تجمع هذه الخوارزمية بين المعالج الكمي وإجراءات التحسين الكلاسيكية لأداء عدة عمليات تشغيل قصيرة تكون سريعة بما يكفي لتجنب الأخطاء. يعد الكمبيوتر الكمومي حالة من التخمينمع سلسلة ansatz الكمومية اعتمادًا على عدة معايير... يتم قياس المصطلحات الفردية للهاميلتوني واحدًا تلو الآخر (أو في مجموعات التنقل باستخدام استراتيجيات أكثر تقدمًا) ، مما يعطي تقديرًا للطاقة المتوقعة لمتجه معين من المعلمات. ثم يتم تحسين المعلمات من خلال إجراء التحسين الكلاسيكي حتى التقارب. لقد تم توسيع النهج التغيري ليشمل العديد من المشاكل الخوارزمية إلى جانب المحاكاة الكمومية.
يجب أن تكون أجهزة الكمبيوتر الكمومية التي يمكنها محاكاة الأنظمة الكيميائية الكبيرة متسامحة مع الأخطاء من أجل تنفيذ خوارزميات عميقة بشكل تعسفي دون أخطاء. مثل هذا الكمبيوتر الكمومي قادر على محاكاة نظام كيميائي عن طريق تعيين سلوك إلكتروناته مع سلوك الكيوبتات والبوابات الكمومية. عملية النمذجة الكمومية بسيطة للغاية من الناحية المفاهيمية وهي موضحة في الشكل 2 (أ). سنقوم بإعداد سجل للكيوبتات يمكنه تخزين الدالة الموجية وتنفيذ التطور الأحادي لهاملتونيانباستخدام أساليب النمذجة الهاميلتونية ، والتي تمت مناقشتها أدناه. باستخدام هذه العناصر ، يكون الروتين الفرعي الكمي المعروف باسم تقدير المرحلة الكمومية قادرًا على العثور على المتجهات الذاتية والقيم الذاتية للنظام. على وجه التحديد ، إذا كان سجل الكيوبت في البداية في الحالة | 0⟩ ، ستكون الحالة النهائية: بمعنى آخر ، الحالة النهائية هي تراكب للقيم الذاتية

والمتجهات الذاتية الأنظمة. ثم يتم قياس الحالة الأرضية بالاحتمال... لتعظيم هذا الاحتمال ، يتم إنشاء حالة خط الأساس باعتبارها حالة سهلة التحضير ولكن أيضًا حالة ذات دوافع جسدية من المتوقع أن تكون مماثلة للحالة الأساسية بالضبط. مثال نموذجي هو حالة Hartree-Fock ، على الرغم من استكشاف أفكار أخرى للأنظمة شديدة الارتباط [انظر المرجع. هنا ].
هناك طريقتان شائعتان لتمثيل الإلكترونات في الجزيء: الطرق القائمة على الشبكة والمدارية أو الطرق الأساسية (انظر McArdle وزملاؤه للحصول على تحليل كامل [ هنا ]). في طرق مجموعة الأساس ، يتم تمثيل دالة موجة الإلكترون كمجموع محددات سلاتر لمدارات الإلكترون ، والتي يمكن مقارنتها مباشرة مع سجل كيوبت [ هنا وهنا ]. هذا يتطلب اختيار الأساس والحساب الأولي للتكاملات الإلكترونية. من ناحية أخرى ، في طرق الشبكة ، تتم صياغة المشكلة كحل لمعادلة تفاضلية عادية في شبكة. ميزة النمذجة القائمة على الشبكة هي أنه لا يلزم تقريب Bourne-Oppenheimer أو مجموعة أساسية. ومع ذلك ، فهي ليست غير متماثلة بشكل طبيعي ، وهو ما يتطلبه مبدأ باولي من ميكانيكا الكم ، لذلك من الضروري التأكد من عدم التناسق باستخدام إجراء الفرز [ هنا ]. تمت مناقشة الطرق المستندة إلى الشبكة في سياق محاكاة الديناميات الكيميائية [cf. هنا ] وحساب ثابت المعدل الحراري [انظر. هنا]. على الرغم من الاختلافات ، فإن سير عمل النمذجة الكمومية متطابق ، كما هو موضح في الشكل 2.
هناك أيضًا عدة طرق لبناء المشغل... سوف نقدم أبسط تقنية ، التروترة ، والمعروفة أيضًا باسم صياغة المنتج [انظر ص. هنا ] ؛ لمحة كاملة انظر [ هنا و هنا ]. يعتمد التروت على فرضية أن الجزيئي هاميلتوني يمكن تقسيمه كمجموع المصطلحات التي تصف تفاعلات إلكترون واحد واثنين. إذا كان الأمر كذلك ، فعندئذٍ عامل التشغيليمكن تنفيذها من حيث العوامل المقابلة لكل مصطلح في هاملتونيان باستخدام معادلة تروتر - سوزوكي [ هنا ]: على سبيل المثال ، في التكمية الثانية ، سيكون لكل مصطلح في هذا التعبير الشكل أو ، حيث توجد عوامل الإبادة والخلق ، على التوالي. قدم ويتفيلد وزملاؤه إنشاءات مخطط تفصيلية وصريحة تمثل هذه المصطلحات [راجع. هنا ]. بعد احتساب الأعضاء
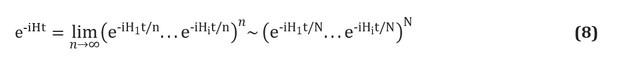

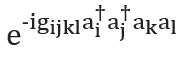
 و المعروفة باسم التكاملات الإلكترونية ، الكميةعازم تماما. يمكنك أيضًا استخدام صيغ Trotter - Suzuki ذات الترتيب الأعلى لتقليل الخطأ. هناك العديد من تقنيات النمذجة الهاملتونية الأخرى. من أمثلة التقنيات القوية والمعقدة التكعيب [ هنا ] ومعالجة الإشارات الكمية [انظر المرجع. هنا ] ، والتي لها مقياس مقارب مثالي ، على الرغم من أنه من غير الواضح ما إذا كان هذا سيؤدي إلى تطبيقات عملية أفضل.
و المعروفة باسم التكاملات الإلكترونية ، الكميةعازم تماما. يمكنك أيضًا استخدام صيغ Trotter - Suzuki ذات الترتيب الأعلى لتقليل الخطأ. هناك العديد من تقنيات النمذجة الهاملتونية الأخرى. من أمثلة التقنيات القوية والمعقدة التكعيب [ هنا ] ومعالجة الإشارات الكمية [انظر المرجع. هنا ] ، والتي لها مقياس مقارب مثالي ، على الرغم من أنه من غير الواضح ما إذا كان هذا سيؤدي إلى تطبيقات عملية أفضل.
4. مشاكل التحسين
يمكن صياغة العديد من المشكلات في علم الأحياء الحسابي والتخصصات الأخرى على أنها إيجاد الحد الأدنى أو الأقصى العالمي لوظيفة معقدة متعددة الأبعاد. على سبيل المثال ، يُعتقد أن التركيب الأصلي للبروتين هو الحد الأدنى العالمي لسطحه الفائق للطاقة الحرة [انظر. هنا ]. في منطقة أخرى ، فإن تحديد المجموعات في شبكة من البروتينات أو الكائنات البيولوجية المتفاعلة يعادل إيجاد مجموعة فرعية مثالية من العقد [انظر. هنا]. لسوء الحظ ، باستثناء بعض الأنظمة البسيطة ، غالبًا ما تكون مشكلات التحسين معقدة للغاية. على الرغم من وجود طرق إرشادية لإيجاد حلول تقريبية ، إلا أنها عادةً ما تعطي حدودًا دنيا محلية فقط ، وفي كثير من الحالات يكون حتى الاستدلال غير قابل للتقرير. تم فحص قدرة أجهزة الكمبيوتر الكمومية على تسريع الحلول لمشكلات التحسين هذه أو إيجاد حلول أفضل بالتفصيل.
يعد موضوع التحسين في الكمبيوتر الكمومي معقدًا لأنه غالبًا ما يكون من غير الواضح ما إذا كان الكمبيوتر الكمي يمكنه توفير أي نوع من التسريع. في هذا القسم ، سوف نقدم لمحة عامة عن بعض أفكار التحسين الكمي. ومع ذلك ، فإن ضمانات التحسين ليست واضحة جدًا عند مقارنتها ، على سبيل المثال ، بالمحاكاة الكمية ، والتي من المتوقع أن تكون مفيدة على المدى الطويل.
4.1 التحسين في المعالج الكمي
يعد التحسين الكيميائى الكمى أحد أكثر طرق التحسين شيوعًا نظرًا لوجود آلات D-Wave [انظر. هنا ] التي تنفذ هذا النهج في البداية. تستند الحوسبة الكمومية Adiabatic [ هنا ] إلى النظرية الثابتة لميكانيكا الكم [cf. هنا]. وفقًا لهذه النظرية ، إذا تم إعداد نظام في الحالة الأرضية لهاملتونيان ، وتغير هاملتونيان ببطء إلى حد ما ، فسيظل النظام دائمًا في حالته الأرضية الآنية. يمكن استخدام هذا لإجراء العمليات الحسابية عن طريق ترميز مشكلة (مثل وظيفة التسجيل التي نأمل في تقليلها) باعتبارها هاميلتوني ، والتطور التدريجي نحو هذا الهاميلتوني من بعض الأنظمة الأصلية التي يمكن تحضيرها بشكل تافه في حالتها الأساسية. بشكل عام ، يتم التعبير عن التطور الثابت على النحو التالي: هنا

و - وظائف من هذا القبيل و لفترة معينة T. على سبيل المثال ، يمكننا التفكير في برنامج التلدين الخطي باستخدام و ... تم تخصيص العديد من الأعمال لمناقشة وقت تنفيذ خوارزمية ثابت الحرارة ، ولكن الاستدلال العام هو أن وقت التنفيذ يتناسب إلى أقصى حد مع المربع العكسي لأدنى فجوة طيفية (أصغر فرق طاقة بين الأرض والحالات المثارة الأولى) أثناء التطور ثابت الحرارة... يُعتقد أن الحوسبة الكمومية الثابتة (والحوسبة الكمومية بشكل عام) ليست قادرة على حل فئة المشاكل الكاملة للـ NP بشكل فعال ، أو على الأقل لم تصمد أي من هذه الطرق لاختبار صارم [انظر المرجع. هنا ].
من حيث المبدأ ، فإن الحوسبة الكمومية الثابتة تعادل الحوسبة الكمومية الشاملة [cf. هنا ]. تحدث هذه العالمية فقط إذا سمح التطور بعدم العشوائية ، مما يعني أن هاميلتوني لديه عناصر غير سلبية خارج القطر في مرحلة ما من التطور. التطبيق التجريبي الأكثر شيوعًا للحوسبة الكمومية الثابتة ، الذي تم تسويقه بواسطة D-Wave Systems Inc.، يستخدم سكان هاميلتونيون العشوائي ، وبالتالي فهو ليس عالميًا. هناك بعض القلق في الأدبيات المهنية من أن هذه المجموعة المتنوعة من الحوسبة الكمومية قد تكون محاكاة كلاسيكية [ هنا ] ، مما يعني أن التسارع الأسي قد لا يكون ممكنًا. على الرغم من هذه المخاوف ، فقد تم استخدام هذه التقنية على نطاق واسع كتقنية تحسين metaheuristic وقد ثبت مؤخرًا أنها متفوقة على التلدين المحاكي [انظر المرجع. هنا ].
تمت دراسة التحسين الكمي خارج نموذج ثابت الحرارة. خوارزمية التحسين التقريبي الكمومي (QAOA) [راجع. هنا أن ، هنا و هنا] هي خوارزمية أمثلية متغيرة في كمبيوتر كمي ولدت اهتمامًا كبيرًا بالأدبيات. كانت هناك عدة تطبيقات تجريبية لـ QAOA في المعالجات الكمومية ، على سبيل المثال [see. هنا ] الشكل 3. الشكل 3. (أ) محاكاة حاسوب كمي ثابت الحرارة ينفذ مشكلة طي البروتين المبسطة الموصوفة [ هنا ]. اللون يشفر الاحتمال اللوغاريتمي العشري لسلسلة ثنائية معينة. في نهاية الحساب ، يكون احتمال قياس حلين أقل طاقة بالقرب من 0.5. التطور لا يكون أبدًا ثابتًا ثابتًا تمامًا في وقت محدود ، والسلاسل الثنائية الأخرى لها احتمالات قياس متبقية. (ب)

وصف العملية الثابتة للحساب الكمي. تتغير احتمالية تحريك الكيوبتات ببطء ، مما يؤدي إلى تدويرها. لاحظ أن تمثيل كرة بلوخ غير مكتمل لأنه لا يعرض الارتباطات بين الكيوبتات المختلفة المطلوبة لميزة الكم. في نهاية التطور ، يكون نظام الكيوبت في حالة كلاسيكية (أو تراكب للحالات الكلاسيكية) ، يمثل الحل بأقل طاقة. (ج) مستويات الطاقة أثناء التطور الكمي ثابت الحرارة. يتم تحديد مقدار الوقت اللازم لضمان التطور شبه الثابت من خلال الحد الأدنى من فرق الطاقة بين المستويات ، والذي يشار إليه بالخط المتقطع
4.2 تنبؤ بنية البروتين
يظل التنبؤ ببنية البروتين بدون مصفوفة مشكلة رئيسية مفتوحة لم يتم حلها في علم الأحياء الحسابي. سيجد حل هذه المشكلة تطبيقًا واسعًا في الهندسة الجزيئية وتصميم الأدوية. وفقًا لفرضية طي البروتين ، فإن التركيب الأصلي للبروتين يعتبر الحد الأدنى العالمي من طاقته الحرة [انظر. هنا ] ، على الرغم من وجود العديد من الأمثلة المضادة. بالنظر إلى مساحة التوافق الشاسعة المتاحة حتى بالنسبة للببتيدات الصغيرة ، فإن المحاكاة الكلاسيكية الشاملة غير قابلة للحل. ومع ذلك ، يتساءل الكثيرون عما إذا كانت الحوسبة الكمية يمكن أن تساعد في حل هذه المشكلة.
تركز أدبيات الحوسبة الكمومية على نموذج الشبكة البروتينية ، حيث يتم نمذجة الببتيد على أنه بنية شبكية ذاتية الدفع ، على الرغم من أن العديد من النماذج الأخرى قد بدأت مؤخرًا في تطبيقها في الممارسة الحسابية [راجع. هنا ]. يتوافق كل موقع شبكي مع بقايا ، وتساهم التفاعلات بين المواقع المجاورة المكانية في وظيفة الطاقة. هناك عدة مخططات لتلامس الطاقة ، ولكن تم استخدام اثنين فقط في التطبيقات الكمية: النموذج القطبي الكارهة للماء [انظر. هنا ] ، والذي يعتبر فئتين فقط من الأحماض الأمينية ، ونموذج ميازاوا-جيرنيجان [راجع. هنا] ، التي تحتوي على تفاعلات لكل زوج من المخلفات. في حين أن هذه النماذج هي تبسيط ملحوظ ، إلا أنها قدمت نظرة ثاقبة في طي البروتين [انظر المرجع. هنا ] وتم اقتراحها كأداة بدائية لدراسة الفضاء المطابق قبل مزيد من التنقيح التفصيلي [انظر. هنا أن و هنا ].
ركز كل العمل تقريبًا على الحوسبة الكمية الثابتة ، نظرًا لأن الببتيدات النموذجية تتطلب عددًا كبيرًا من الكيوبتات ، وآلات الكم D-Wave هي أكبر الأجهزة الكمية المتاحة اليوم.
ومع ذلك ، في مقال نشر مؤخرًا بقلم Fingerhat وزملائه [انظر هنا] جرت محاولة لوصف استخدام خوارزمية ضمان الجودة. كلتا الطريقتين لهما خصائص متشابهة إذا تم ترميز مشكلة الشبكة البروتينية كمشغل هاميلتون. تم اعتبار هذه الطريقة لأول مرة بواسطة Perdomo [انظر. هنا ] ، الذي اقترح استخدام سجل كيوبتلتشفير الإحداثيات الديكارتية للأحماض الأمينية N على شبكة مكعبة الأبعاد D مع جوانب N. يتم التعبير عن وظيفة الطاقة في Hamiltonian تحتوي على مصطلحات لمكافأة جهات الاتصال مع البروتينات: الحفاظ على البنية الأساسية وتجنب تطابق الأحماض الأمينية بعد فترة وجيزة من هذه المقالة التاريخية ، ظهر مقال آخر يناقش بناء نماذج أكثر كفاءة بتات لشبكة ثنائية الأبعاد [انظر. هنا ].
تم اختبار هذه الترميزات على أجهزة حقيقية في عام 2012 عندما كان Perdomo وزملاؤه [see. هنا] حسبت أقل تشوه للطاقة لببتيد PSVKMA على آلة الكم D-Wave. قام فريق باباي البحثي مؤخرًا بتوسيع نطاق الدوران وتشفير الألماس للنماذج ثلاثية الأبعاد وأدخل تحسينات حسابية تقلل من تعقيد وسرعة حركة ترميز هاملتون [انظر المرجع. هنا ]. استخدموا معالج D-Wave 2000Q لتحديد الحالة الأرضية لهيجولين (10 بقايا) على شبكة مربعة والتربتوفان (8 بقايا) على شبكة مكعبة ، وهي أكبر ببتيدات تم فحصها حتى الآن. تستخدم هذه التطبيقات التجريبية طريقة يتم فيها إصلاح جزء من الببتيد. هذا يسمح بإدخال مشاكل كبيرة في الكمبيوتر الكمومي بسبب إمكانية البحثعدد معلمات المشكلة المدروسة.
يعد العثور على التشكل الأقل طاقة في النموذج الشبكي مشكلة NP صعبة [راجع. هنا و هنا ]، مما يعني أنه في ظل الفرضيات القياسية لا يوجد خوارزمية الكلاسيكية لحل. بالإضافة إلى ذلك ، يُعتقد حاليًا أن أجهزة الكمبيوتر الكمومية لا يمكنها تقديم تسريع أسي لمشكلات NP كاملة وأكثر تعقيدًا [cf. هنا ] ، على الرغم من أنها قد تقدم فوائد القياس ، والتي تُعرف في الأدبيات باسم "التسارع الكمي المحدود" [cf. هنا]. في الآونة الأخيرة ، طبقت مجموعة أوترل البحثية عمليات المحاكاة العددية للتحقيق في هذه الحقيقة ، وخلصت إلى أن هناك دليلًا على محدودية التسارع الكمي ، على الرغم من أن هذه النتيجة قد تتطلب آلات ثابتة الحرارة تستخدم تصحيح الخطأ أو المحاكاة الكمومية في آلات الأغراض العامة المتسامحة مع الأخطاء [راجع. هنا ].
على الرغم من أن معظم الأدبيات ركزت على نموذج الشبكة البروتينية ، إلا أن مقالة حديثة [ هنا ] حاولت استخدام التلدين الكمي لأخذ عينات دوارة في وظيفة طاقة رشيد [انظر المرجع هنا ]. استخدم المؤلفون معالج D-Wave 2000Qللعثور على تحجيم يبدو ثابتًا تقريبًا مقارنةً بالتلدين التقليدي. تم تقديم نهج مشابه جدًا من قبل مجموعة مارشاند [انظر. هنا ] لمجموعة مختارة من المطابقين.
الاستنتاجات
يمكن للحاسوب الكمومي تخزين ومعالجة كميات هائلة من المعلومات ، وتنفيذ الخوارزميات بمعدل أسرع أضعافا مضاعفة من أي تقنية حوسبة تقليدية. يمكن لإمكانات أجهزة الكمبيوتر الكمومية الصغيرة أن تتفوق بأمان على أفضل أجهزة الكمبيوتر العملاقة الموجودة اليوم ، والتي يمكن أن يكون لها في النهاية تأثير تحولي على البيولوجيا الحسابية ضمن مهام معينة ، مما يعد بتحويل المشكلات من غير قابلة للحل إلى صعبة ومعقدة إلى روتينية. من المتوقع أن تظهر أولى المعالجات الكمومية التي يمكنها حل المشكلات المفيدة خلال العقد القادم. لذلك ، فإن فهم ما يمكن لأجهزة الكمبيوتر الكمومية أن تفعله وما لا تستطيع فعله هو أولوية لكل عالم حسابي.
على الرغم من أننا ندخل للتو عصر الحوسبة الكمية العملية ، إلا أنه يمكننا بالفعل رؤية ملامح بيولوجيا حاسوبية كمومية جديدة للعقود القادمة. نأمل أن تثير هذه المراجعة اهتمام علماء الأحياء الحاسوبية بالتقنيات التي قد تغير قريبًا مجال تجاربهم وأبحاثهم. والمتخصصون في الحوسبة الكمومية ، بدورهم ، سيكونون قادرين على مساعدة علماء الأحياء على تطوير مستوى البيولوجيا الحاسوبية والمعلوماتية الحيوية بشكل كبير ، والتي من المتوقع أن تحقق العديد من النتائج المهمة للبشرية جمعاء.