يتم التعبير عن الممانعة المميزة لخط ضياع بالصيغة المعروفة:
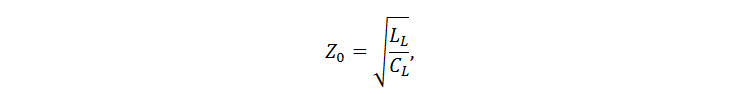
حيث L L و C L هما المحاثة الخطية والسعة الخطية (أي لكل وحدة طول). أعتقد أنه سيكون من المفيد توضيح مصدرها. لنأخذ في الاعتبار قسمًا صغيرًا للغاية من خط نقل طويل بسلكين ، يتدفق من خلاله تيار متناوب (الشكل 1). التيار متناوب ، وبالتالي فإن القيم اللحظية للتيار ، والجهد بين الأسلاك ، والكثافة الخطية للشحنة الكهربائية تتغير على طول الأسلاك.
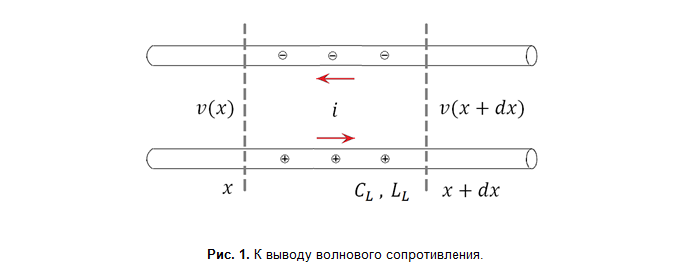
قانون حفظ الشحنة لقسم الأسلاك وقانون فاراداي للدائرة كالتالي:

بالنسبة للخط بدون خسائر (R L = 0) ومع مراعاة Φ L = L L ∙ i و q L = C L ∙ v نحصل على:
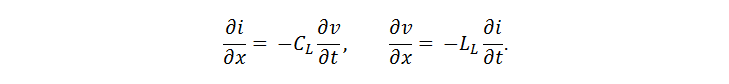
يتم تقليل هذه المعادلات التفاضلية إلى شكل موجة ، والتي نحصل عليها:
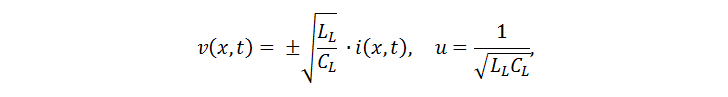
حيث u هي سرعة انتشار الموجة ، والمعامل الذي يربط التيار في الأسلاك والجهد بين الأسلاك هو الممانعة المميزة. فيما يلي بعض النسب المفيدة (TD - تأخير وقت الخط):
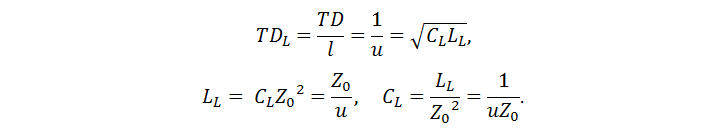
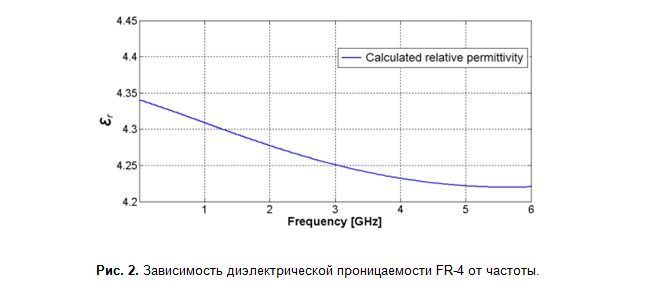
السعة والتحريض يعتمدان على التردد ، وبالتالي فإن الممانعة المميزة تتغير مع التردد. يقتصر تأثير تأثير الجلد على الحث على ترددات تصل إلى عدة عشرات من ميغا هرتز ، في نطاق التردد العلوي يتغير بشكل ضئيل. تتأثر قيمة السعة باعتماد ثابت العزل الكهربائي لمادة لوحة الدائرة المطبوعة على التردد ، ولخطوط microstrip ، بسبب عدم تناسق العازل ، وكذلك تأثير التشتت. تختلف بيانات الألياف الزجاجية FR-4 في مصادر مختلفة ، ومع ذلك ، كتقدير ، يمكن افتراض أن ثابت العزل الكهربائي ينخفض بمقدار 0.15-0.2 كل عقد (الشكل 2). يرجع الاختلاف في البيانات إلى حقيقة أن FR-4 هي فئة مادية. يتكون من الألياف الزجاجية وراتنج الإيبوكسي ، والتي لها ثوابت عازلة مختلفة بشكل كبير (الشكل 3).كلما زاد عدد الراتنج الموجود في المادة ، قلت القيمة المتوسطة الحجم لثابت العزل الكهربائي لرقائق الألياف الزجاجية. وبالتالي ، قيم مختلفة لمختلف الشركات المصنعة. بالمناسبة ، بسبب هذا التباين ، يعتمد ثابت العزل الكهربائي أيضًا على الاتجاه - الطولي أو العرضي ، مما يؤثر على حسابات الخطوط التفاضلية ، نظرًا لأن تكوين المجال سيختلف اعتمادًا على الوضع.

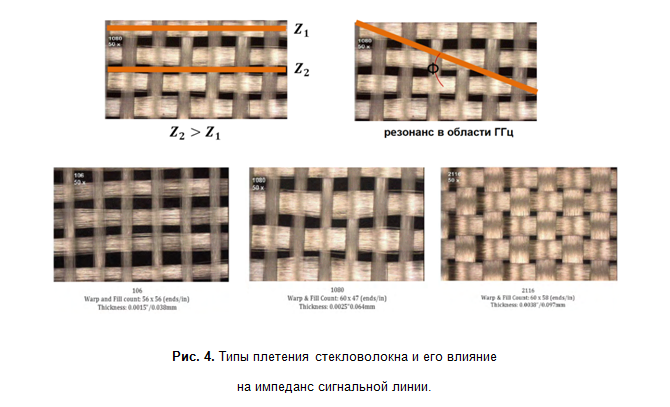
يؤثر الترتيب المتبادل للألياف الزجاجية والألياف الموصلة أيضًا على الممانعة المميزة. إذا كان الموصل يقع فوق الألياف ، فإن الممانعة المميزة لها ستكون أعلى قليلاً مقارنة بالموصل المجاور ، الذي وقع في الفجوة بين الألياف. إذا تم توجيه الموصل بزاوية للألياف ، فإن هذا يؤدي إلى تغيير دوري في الممانعة المميزة وتأثيرات الرنين عند الترددات في منطقة عشرات GHz. تعتمد درجة التأثير بشكل كبير على نوع نسيج الألياف الزجاجية (الشكل 4). هذا هو السبب في وجود مواد متخصصة للوحات الدوائر المطبوعة عالية التردد ، حيث يصبح تأثير هذه التأثيرات كبيرًا. تتمتع معلمات هذه العوازل باستقرار أفضل على نطاق تردد واسع وموثقة بشكل أفضل.
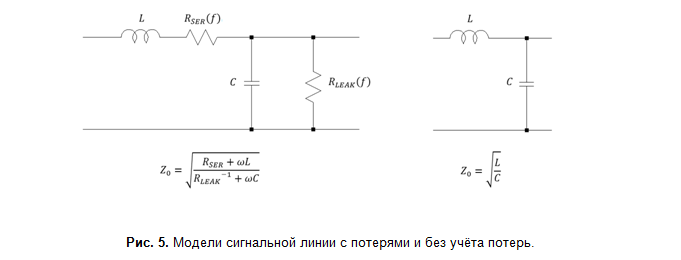
فيما يتعلق بالخسائر (الشكل 5) ، في معظم الحالات العملية ، يكون نموذج الخسارة المنخفضة قابلاً للتطبيق ، حيث يمكن إهمال الخسائر عند الترددات العالية R SER ، L ، R LEAK 1⁄ωC. أتاح هذا التبسيط إمكانية تطوير نماذج فعالة تسمح بحساب دقيق للغاية لمعلمات خط الإشارة باستخدام وظائف قياسية.
تم اختراع خطوط الإشارة المستوية في أوائل الخمسينيات من القرن الماضي ، وتم تطوير نماذج رياضية دقيقة على الفور تقريبًا لخطوط الشريط ، واستغرق الأمر عدة عقود لإنشاء نموذج تحليل دقيق لشريط دقيق. وكان هارولد ويلر واحدة من أولى (في 1965) ل تقديم حلول دقيقة لحالات معينة ، وهو ما المعمم في وقت لاحق (عام 1977) . والسبب هو عدم تناسق المادة العازلة ، مما يؤدي إلى توزيع معقد للمجال الكهربائي ، والذي يعتمد أيضًا على التردد.
بطبيعة الحال ، لم يكن هذا النموذج هو الوحيد - وبحلول عام 1988 كان هناك ما يكفي منها لجعل المقارنة بينها ممتعة. تم ذلكالعظيم والرهيب إيريك بوغاتين. صادفت هذا المقال عندما كنت أختار نموذج حساب لآلة حاسبة. ثم وصلت إلى منشورات ويلر ، حيث يوجد العديد من صفحات الرياضيات الرائعة مع التحولات المطابقة ، وأدركت أن بوغاتين لم يقرأها بعناية (أو لم يقرأها على الإطلاق) وكان فظًا في نموذجه ، مما أثر على نتائج المقارنة. ثم هذا الخطأ هاجر إلى عام 2007. في الوقت نفسه ، يشير بوغاتين نفسه إلى دراسة "بيانات مقاومة خط نقل الميكروويف" من قبل M.A.R. Gunstan ، لكنني لم أعد أحفر حيث تنمو الأرجل ، معترفًا بالرفيق بوغاتين باعتباره الجاني (الذي ، بالمناسبة ، أحترمه كثيرًا ، بوغاتين هو القوة).
لذلك ما هي النقطة. قام بوغاتين بشكل تجريبي بقياس السعة الخطية لخطوط microstrip ذات عروض مختلفة (بتردد 1 كيلو هرتز) وقارنها مع القيم المحسوبة (الشكل 6).
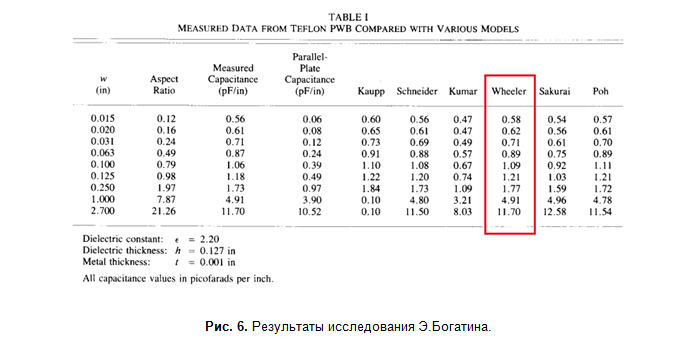
في جميع النماذج التي درست منها المصادر الأولية ، تم إعطاء العلاقات التحليلية لمقاومة الموجة. يتم حساب السعة باستخدام النسبة التالية:
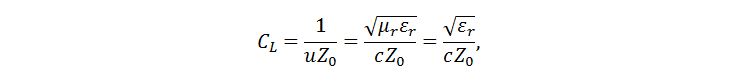
حيث ε r هو ثابت العزل ، c هي سرعة الضوء. يؤدي عدم تناسق العازل الكهربائي إلى حقيقة أنه من الضروري اختراع القيمة الفعالة لثابت العزل الكهربائي. كتب بوغاتين:
في حالة ويلر [13] ، لم يتم تقديم نموذج لثابت العزل الكهربائي الفعال. ومع ذلك ، بناءً على اقتراح Gunsten [6] ، فإن مخطط نموذج Wheeler يستخدم ثابت العزل الكهربائي الفعال من نموذج Schneider.
ويستخدم نموذج Wheeler-Schneider الهجين (ينتج عنه pF / بوصة):
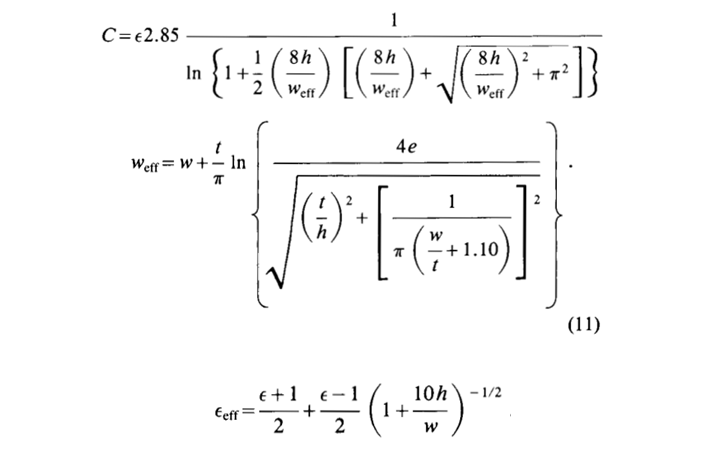
وبحسب نتائج التجربة فإن النموذج يعطي دقة جيدة ويثني بوغاتين على دراجته المخترعة:
تم العثور على مزيج من نموذج ويلر وشنايدر يتفق مع البيانات المنشورة السابقة والبيانات الجديدة المقدمة هنا بنسبة أفضل من 3 في المائة ، وهي ذات شكل مناسب للاستخدام في ورقة انتشار. بالإضافة إلى كونه مفيدًا لمحاكاة الكمبيوتر لتصميمات معينة ، يمكن لهذا النموذج أن يقدم بعض الأفكار المفيدة التي تضيف إلى حدس مهندسي التصنيع والتصميم
الآن دعنا ننتقل إلى المصدر الأصلي. الصيغ التي يستخدمها بوغاتين هي صيغ مبسطة للحالة بدون عازل:
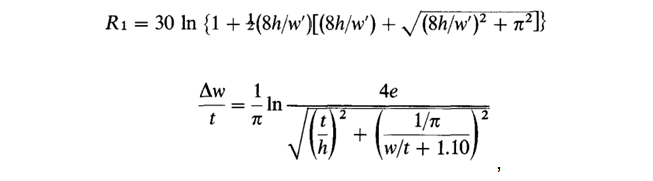
والنموذج الكامل يبدو كالتالي:
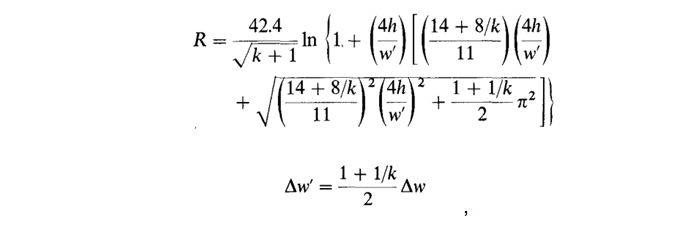
هنا ، في تدوين ويلر ، R هي مقاومة الموجة ، k هو ثابت العزل ، R 1 = R (k = 1) هي المقاومة بدون عازل ، ∆w هي تصحيح العرض مع الأخذ بعين الاعتبار سمك الموصل ، ∆w 'هو التصحيح مع الأخذ في الاعتبار تأثير العازل. يستخدم ويلر الرمز k 'لثابت العزل الكهربائي الفعال ويعطيه الصيغة التالية:
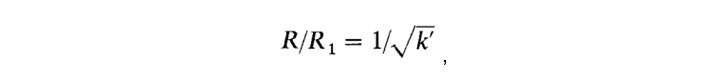
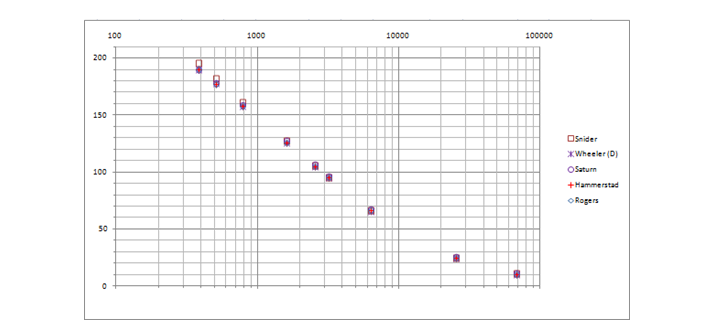
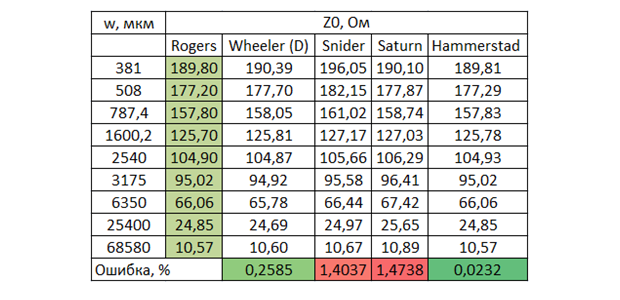
وهو ليس بهذه البساطة ، بالطبع ، مثل شنايدر ، لكنه مع ذلك في النموذج. كررت حسابات بوغاتين ، وتركت النماذج الأكثر دقة: شنايدر ، ويلر ، نسختهم الهجينة - وأضفت نتائج الحساب باستخدام آلة حاسبة Saturn PCB Toolkit ونموذج Hammerstead . من أجل الوضوح ، أقدم رسمًا بيانيًا وبيانات جدولية بها خطأ متعلق بالبيانات التجريبية.
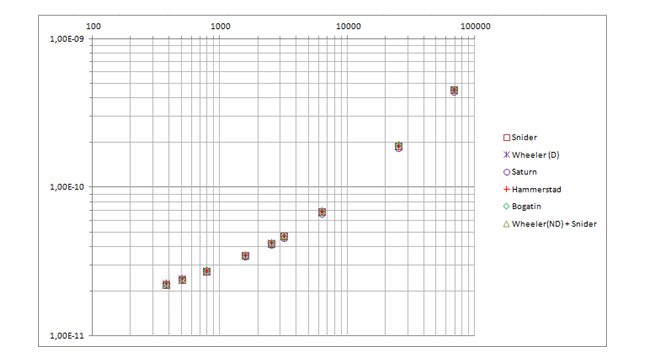
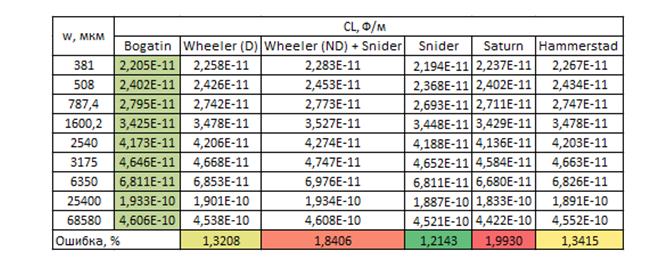
مع الأخذ في الاعتبار أخطاء القياس وثابت العزل الكهربائي للمادة الأساسية (2.2 ± 1٪) ، يمكننا القول أن جميع النماذج ترتبط جيدًا بالبيانات التجريبية ، فليس عبثًا أن قام الباحثون بتعديل الصيغ لسنوات. كنت أتوقع المزيد من الدقة من زحل ، حيث تقول مباشرة إنها تستخدم صيغة "ليست بسيطة ، ولكنها معقدة" والدقة مماثلة لـ Sonnet 3D. بالإضافة إلى ذلك ، لا يمكن تحديد السماكة إلا بالأوقية ، وهذا إما أوقية. (18 ميكرون) ، أو 1 أوقية. (35 ميكرومتر) ، و 1 مل (25.4 ميكرومتر) غير محدد. القيم الواردة في الجدول هي لـ أوقية. ، لأنها أقرب إلى البيانات التجريبية التي تم الحصول عليها بهذه الطريقة. من الواضح أيضًا أن نموذج ويلر الأصلي كان سيكون أكثر دقة في هذه العينة من البيانات ، لذلك كنت منزعجًا منه. خاصة بالنظر إلى ذلكأن نموذج شنايدر نفسه له عيب خطير - فهو لا يأخذ في الاعتبار تأثير سماكة الموصل ، والتي لا تؤثر تقريبًا على السعة ، ولكنها مهمة للحث ، وبالتالي مقاومة الموجة نفسها. للأسف ، بوجاتين لا يعطي قيمة مقاومة الموجة ، لذلك اعتادآلة حاسبة من شركة مرموقة روجرز. زحل هذه المرة هو 1 أوقية. أعطت دقة أفضل إلى حد ما ، منطق عملها ليس واضحًا جدًا بالنسبة لي حتى الآن. يوضح الرسم البياني أنه مع انخفاض العرض (حيث يزداد تأثير السُمك) ، يسقط شنايدر. ويبدو أن روجرز يعتمد على نموذج هامرستيد. أنا أصلا لم على ويلر ، ولكن لأن معظم الآلات الحاسبة المتطورة هي على Hammerstead، سيكون من الممكن للتبديل إلى هذا النموذج من أجل مواكبة لها (على الرغم من أن النموذج لا يكون لها صيغة واضحة لتخليق، خلافا لويلر).
في الواقع ، في هذا أعتبر أن العدالة قد استُعيدت. ويلر قوة. حتى بوغاتين يخطئ أحيانًا لذلك لا تثق ، تحقق وتحقق جيدًا. استخدم حسابات خطوط الإشارة الخاصة بك. بالمناسبة. يرجى المشاركة في التعليقات إذا كنت تستخدم حساب مقاومة الموجة وإذا كان الأمر كذلك ، فما هي المساعدة؟
ملاحظة: أنا بصدد العمل على الآلة الحاسبة وأنا بصدد الانتهاء من الكتاب ، والآن وصلت يدي إلى الإصدار المجاني - لقد أضفت جميع التحسينات والإصلاحات التي تم إجراؤها مسبقًا بالكامل فقط. حظا موفقا للجميع!