TensorFlow.js: الجزء 1: استخدام واجهة برمجة التطبيقات ذات المستوى المنخفض لتقريب الوظائف الخطية

فوائد استخدام TensorFlow.js في المتصفح

• التفاعلية - يحتوي المتصفح على العديد من الأدوات لتصور العمليات الجارية (رسومات ، رسوم متحركة ، إلخ) ؛
• أجهزة الاستشعار - يتمتع المتصفح بإمكانية الوصول المباشر إلى مستشعرات الجهاز (الكاميرا ونظام تحديد المواقع العالمي ومقياس التسارع وما إلى ذلك) ؛
• أمان بيانات المستخدم - ليست هناك حاجة لإرسال البيانات المعالجة إلى الخادم ؛
• التوافق مع النماذج التي تم إنشاؤها في Python .

أداء

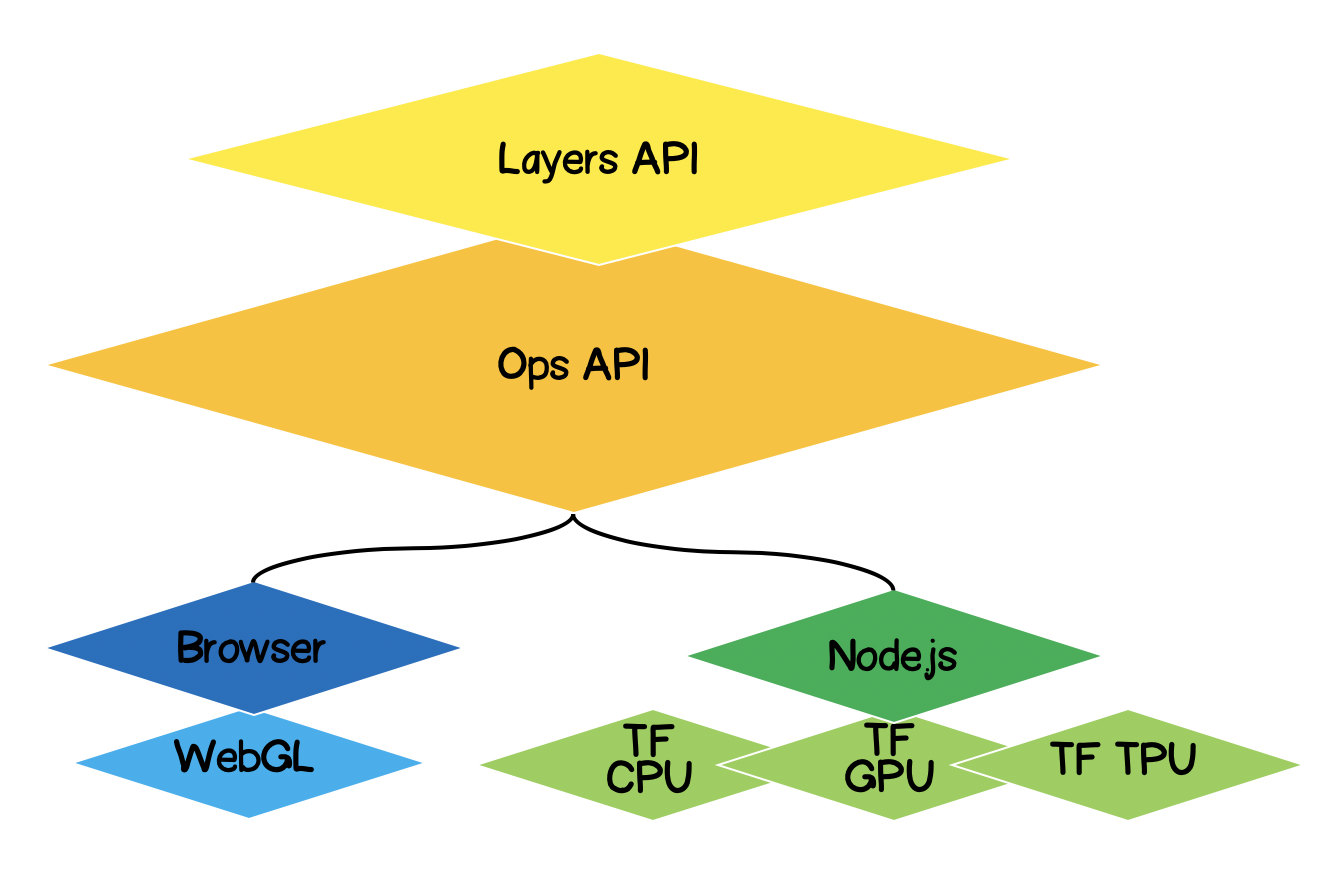
هندسة TensorFlow.js

1. الطبقة الدنيا - هذه الطبقة مسؤولة عن موازنة العمليات الحسابية عند إجراء عمليات حسابية على الموترات.
2. Ops API - يوفر واجهة برمجة التطبيقات (API) لأداء العمليات الحسابية على التنسورات.
3. Layers API - يسمح لك بإنشاء نماذج معقدة من الشبكات العصبية باستخدام أنواع مختلفة من الطبقات (كثيفة ، تلافيفية). تشبه هذه الطبقة واجهة برمجة تطبيقات Keras Python ولديها القدرة على تحميل شبكات Keras Python سابقة التدريب.

صياغة المشكلة

إضفاء الطابع الرسمي على الحل

• - أوجد التدرج المتجهي بحساب المشتقات الجزئية بالنسبة للمعاملات $$$k^{(j)}, b^{(j)}$؛
• - صحح معاملات المعادلة في الاتجاه المعاكس لاتجاه متجه التدرج. وبالتالي ، سنقلل من وظيفة الخطأ:
  
  
  
  

  $$

  $$k^{(j+1)}=k^{(j)} - \mu \bigtriangledown_{k^{(j)}} L(k^{(j)},b^{(j)})=k^{(j)} - \mu\frac{\partial L(k^{(j)},b^{(j)}) }{\partial k^{(j)}};$$
  
  
  
  
  

  $$

  $$b^{(j+1)}=b^{(j)} - \mu \bigtriangledown_{b^{(j)}} L(k^{(j)},b^{(j)})=b^{(j)} - \mu\frac{\partial L(k^{(j)},b^{(j)}) }{\partial b^{(j)}};$$
  
  
  
  
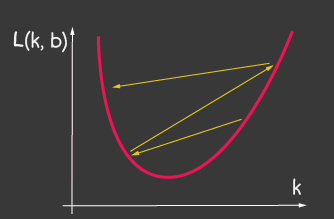
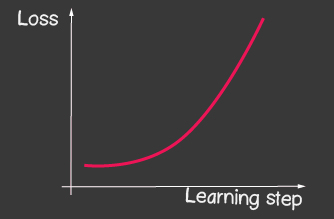
  أين $$$\mu$هو معدل التعلم وهو أحد المعلمات القابلة للتعديل للنموذج. بالنسبة للنسب المتدرج ، فإنه لا يتغير طوال عملية التعلم. يمكن أن تؤدي القيمة الصغيرة لمعدل التعلم إلى تقارب طويل في عملية التعلم الخاصة بالنموذج وضربة محتملة في الحد الأدنى المحلي (الشكل 2) ، ويمكن أن تؤدي القيمة الكبيرة جدًا إلى زيادة لا نهائية في قيمة الخطأ في كل خطوة من خطوات التدريب ، الشكل 1.

الشكل 1: القيمة العالية لمعدل التعلم	الشكل 2: معدل التعلم الصغير

كيفية تنفيذه بدون Tensorflow.js

function loss(ysPredicted, ysReal) {
    const squaredSum = ysPredicted.reduce(
        (sum, yPredicted, i) => sum + (yPredicted - ysReal[i]) ** 2,
        0);
    return squaredSum / ysPredicted.length;
}

    function loss(ysPredicted, ysReal) => {
        const ysPredictedTensor = tf.tensor(ysPredicted);
        const ysRealTensor = tf.tensor(ysReal);
        const loss = ysPredictedTensor.sub(ysRealTensor).square().mean();
        return loss.dataSync()[0];
    };

الحل باستخدام TensorFlow.js

• وضع نموذج (دالة خطية ، في حالتنا) ؛
• وصف دالة الخطأ (في حالتنا ، هذا هو الانحراف المعياري)
• اختر أحد المحسّنين المنفذين (من الممكن توسيع المكتبة بالتنفيذ الخاص بك)

ما هو الموتر

tf.tensor (values, shape?, dtype?)

التصور	وصف
	الترتيب القياسي : 0 الشكل: [] هيكل JS: 2 واجهة برمجة تطبيقات TensorFlow: tf.scalar(2); tf.tensor(2, []);
	رتبة المتجه : 1 الشكل: [4] هيكل JS: [1, 2, 3, 4] واجهة برمجة تطبيقات TensorFlow: tf.tensor([ 1, 2, 3, 4]); tf.tensor([1, 2, 3, 4], [4]); tf.tensor1d([1, 2, 3, 4]);
	رتبة المصفوفة : 2 الشكل: [4،2] هيكل JS: [ [1, 2], [3, 4], [5, 6], [7, 8] ] واجهة برمجة تطبيقات TensorFlow: tf.tensor([[1, 2],[3, 4],[5,6],[7,8]]); tf.tensor([1, 2, 3, ... 7, 8], [4,2]); tf.tensor2d([[1, 2],[3, 4]...[7,8]]); tf.tensor2d([1, 2, 3, ... 7, 8], [4,2]);
	رتبة المصفوفة : 3 الشكل: [4،2،3] هيكل JS: [ [ [ 1, 2], [ 3, 4], [ 5, 6] ], [ [ 7, 8], [ 9, 10], [11, 12] ], [ [13, 14], [15, 16], [17, 18] ], [ [19, 20], [21, 22], [23, 24] ] ] واجهة برمجة تطبيقات TensorFlow: tf.tensor([ [ [ 1, 2], [ 3, 4], [ 5, 6] ], .... [ [19, 20], [21, 22], [23, 24] ] ]); tf.tensor([1, 2, 3, .... 24], [4, 2 ,3])

التقريب الخطي باستخدام TensorFlow.js

import * as tf from '@tensorflow/tfjs';

export default class AbstractRegressionModel {
    constructor(
        width,
        height,
        optimizerFunction = tf.train.sgd,
        maxEpochPerTrainSession = 100,
        learningRate = 0.1,
        expectedLoss = 0.001
    ) {
        this.width = width;
        this.height = height;
        this.optimizerFunction = optimizerFunction;
        this.expectedLoss = expectedLoss;
        this.learningRate = learningRate;
        this.maxEpochPerTrainSession = maxEpochPerTrainSession;

        this.initModelVariables();

        this.trainSession = 0;
        this.epochNumber = 0;
        this.history = [];
    }
}

initModelVariables() {
    throw Error('Model variables should be defined')
}

/**
     * Train model until explicitly stop process via invocation of stop method
     * or loss achieve necessary accuracy, or train achieve max epoch value
     *
     * @param x - array of x coordinates
     * @param y - array of y coordinates
     * @param callback - optional, invoked after each training step
     */
    async train(x, y, callback) {
        const currentTrainSession = ++this.trainSession;
        this.lossVal = Number.POSITIVE_INFINITY;
        this.epochNumber = 0;
        this.history = [];

        // convert array into tensors
        const input = tf.tensor1d(this.xNormalization(x));
        const output = tf.tensor1d(this.yNormalization(y));

        while (
            currentTrainSession === this.trainSession
            && this.lossVal > this.expectedLoss
            && this.epochNumber <= this.maxEpochPerTrainSession
            ) {
            const optimizer = this.optimizerFunction(this.learningRate);
            optimizer.minimize(() => this.loss(this.f(input), output));
            this.history = [...this.history, {
                epoch: this.epochNumber,
                loss: this.lossVal
            }];
            callback && callback();
            this.epochNumber++;
            await tf.nextFrame();
        }
    }

xNormalization = xs => xs.map(x => x / this.width);
yNormalization = ys => ys.map(y => y / this.height);
yDenormalization = ys => ys.map(y => y * this.height);

    /**
     * Calculate loss function as mean-square deviation
     *
     * @param predictedValue - tensor1d - predicted values of calculated model
     * @param realValue - tensor1d - real value of experimental points
     */
    loss = (predictedValue, realValue) => {
        // L = sum ((x_pred_i - x_real_i)^2) / N
        const loss = predictedValue.sub(realValue).square().mean();
        this.lossVal = loss.dataSync()[0];
        return loss;
    };

• لن يتم الوصول إلى الحد الأقصى لعدد التكرارات
• لن تتحقق دقة الخطأ المطلوبة
• لم تبدأ عملية تدريب جديدة

  f(x) {
        throw Error('Model should be defined')
  }

/**
     * Predict value basing on trained model
     *  @param x - array of x coordinates
     *  @return Array({x: integer, y: integer}) - predicted values associated with input
     *
     * */
    predict(x) {
        const input = tf.tensor1d(this.xNormalization(x));
        const output = this.yDenormalization(this.f(input).arraySync());
        return output.map((y, i) => ({ x: x[i], y }));
    }

import * as tf from '@tensorflow/tfjs';

export default class AbstractRegressionModel {
    
    constructor(
        width,
        height,
        optimizerFunction = tf.train.sgd,
        maxEpochPerTrainSession = 100,
        learningRate = 0.1,
        expectedLoss = 0.001
    ) {
        this.width = width;
        this.height = height;
        this.optimizerFunction = optimizerFunction;
        this.expectedLoss = expectedLoss;
        this.learningRate = learningRate;
        this.maxEpochPerTrainSession = maxEpochPerTrainSession;

        this.initModelVariables();

        this.trainSession = 0;
        this.epochNumber = 0;
        this.history = [];
    }

    initModelVariables() {
        throw Error('Model variables should be defined')
    }

    f() {
        throw Error('Model should be defined')
    }

    xNormalization = xs => xs.map(x => x / this.width);
    yNormalization = ys => ys.map(y => y / this.height);
    yDenormalization = ys => ys.map(y => y * this.height);

    /**
     * Calculate loss function as mean-squared deviation
     *
     * @param predictedValue - tensor1d - predicted values of calculated model
     * @param realValue - tensor1d - real value of experimental points
     */
    loss = (predictedValue, realValue) => {
        const loss = predictedValue.sub(realValue).square().mean();
        this.lossVal = loss.dataSync()[0];
        return loss;
    };

    /**
     * Train model until explicitly stop process via invocation of stop method
     * or loss achieve necessary accuracy, or train achieve max epoch value
     *
     * @param x - array of x coordinates
     * @param y - array of y coordinates
     * @param callback - optional, invoked after each training step
     */
    async train(x, y, callback) {
        const currentTrainSession = ++this.trainSession;
        this.lossVal = Number.POSITIVE_INFINITY;
        this.epochNumber = 0;
        this.history = [];

        // convert data into tensors
        const input = tf.tensor1d(this.xNormalization(x));
        const output = tf.tensor1d(this.yNormalization(y));

        while (
            currentTrainSession === this.trainSession
            && this.lossVal > this.expectedLoss
            && this.epochNumber <= this.maxEpochPerTrainSession
            ) {
            const optimizer = this.optimizerFunction(this.learningRate);
            optimizer.minimize(() => this.loss(this.f(input), output));
            this.history = [...this.history, {
                epoch: this.epochNumber,
                loss: this.lossVal
            }];
            callback && callback();
            this.epochNumber++;
            await tf.nextFrame();
        }
    }

    stop() {
        this.trainSession++;
    }

    /**
     * Predict value basing on trained model
     *  @param x - array of x coordinates
     *  @return Array({x: integer, y: integer}) - predicted values associated with input
     *
     * */
    predict(x) {
        const input = tf.tensor1d(this.xNormalization(x));
        const output = this.yDenormalization(this.f(input).arraySync());
        return output.map((y, i) => ({ x: x[i], y }));
    }
}

initModelVariables() {
   this.k = tf.scalar(Math.random()).variable();
   this.b = tf.scalar(Math.random()).variable();
}

tf.variable (initialValue, trainable?, name?, dtype?)

f(x) {
   // y = kx + b
   return  x.mul(this.k).add(this.b);
}

initModelVariables() {
   this.a = tf.scalar(Math.random()).variable();
   this.b = tf.scalar(Math.random()).variable();
   this.c = tf.scalar(Math.random()).variable();
}

f(x) {
    // y = ax^2 + bx + c
    return this.a.mul(x.square()).add(this.b.mul(x)).add(this.c);
}

import * as tf from '@tensorflow/tfjs';
import AbstractRegressionModel from "./AbstractRegressionModel";

export default class LinearRegressionModel extends AbstractRegressionModel {
    initModelVariables() {
        this.k = tf.scalar(Math.random()).variable();
        this.b = tf.scalar(Math.random()).variable();
    }

    f = x => x.mul(this.k).add(this.b);
}

import * as tf from '@tensorflow/tfjs';
import AbstractRegressionModel from "./AbstractRegressionModel";

export default class QuadraticRegressionModel extends AbstractRegressionModel {
    initModelVariables() {
        this.a = tf.scalar(Math.random()).variable();
        this.b = tf.scalar(Math.random()).variable();
        this.c = tf.scalar(Math.random()).variable();
    }

    f = x => this.a.mul(x.square()).add(this.b.mul(x)).add(this.c);
}

import React, { useState, useEffect } from 'react';

import Canvas from './components/Canvas';
import LossPlot from './components/LossPlot_v3';
import LinearRegressionModel from './model/LinearRegressionModel';

import './RegressionModel.scss';

const WIDTH = 400;
const HEIGHT = 400;
const LINE_POINT_STEP = 5;

const predictedInput = Array.from({ length: WIDTH / LINE_POINT_STEP + 1 })
    .map((v, i) => i * LINE_POINT_STEP);

const model = new LinearRegressionModel(WIDTH, HEIGHT);

export default () => {
    const [points, changePoints] = useState([]);
    const [curvePoints, changeCurvePoints] = useState([]);
    const [lossHistory, changeLossHistory] = useState([]);

    useEffect(() => {
        if (points.length > 0) {
            const input = points.map(({ x }) => x);
            const output = points.map(({ y }) => y);

            model.train(input, output, () => {
                changeCurvePoints(() => model.predict(predictedInput));
                changeLossHistory(() => model.history);
            });
        }
    }, [points]);

    return (
        <div className="regression-low-level">
            <div className="regression-low-level__top">
                <div className="regression-low-level__workarea">
                    <div className="regression-low-level__canvas">
                        <Canvas
                            width={WIDTH}
                            height={HEIGHT}
                            points={points}
                            curvePoints={curvePoints}
                            changePoints={changePoints}
                        />
                    </div>
                    <div className="regression-low-level__toolbar">
                        <button
                            className="btn btn-red"
                            onClick={() => model.stop()}>Stop
                        </button>
                        <button
                            className="btn btn-yellow"
                            onClick={() => {
                                model.stop();
                                changePoints(() => []);
                                changeCurvePoints(() => []);
                            }}>Clear
                        </button>
                    </div>
                </div>
                <div className="regression-low-level__loss">
                    <LossPlot
                              loss={lossHistory}/>
                </div>

            </div>
        </div>
    )
}

• لتنفيذ تقريب الوظيفة بواسطة الدالة اللوغاريتمية
• بالنسبة إلى مُحسِّن tf.train.sgd ، حاول اللعب باستخدام LearningRate ولاحظ كيف تتغير عملية التعلم. حاول ضبط معدل التعلم على درجة عالية جدًا للحصول على الصورة الموضحة في الشكل 2.
• اضبط المُحسِّن على tf.train.adam. هل تحسنت عملية التعلم؟ ما إذا كانت عملية التعلم تعتمد على تغيير قيمة LearningRate في منشئ النموذج.