أولاً ، سوف نتعرف بإيجاز على طرق اجتياز الرسوم البيانية ، ونكتب المسار الفعلي ، ثم ننتقل إلى أكثر الطرق اللذيذة: تحسين الأداء وتكاليف الذاكرة. من الناحية المثالية ، يجب عليك تطوير تطبيق لا ينتج عنه قمامة على الإطلاق عند استخدامه.
لقد اندهشت عندما لم يعطيني البحث السطحي تنفيذًا جيدًا واحدًا لخوارزمية A * في C # دون استخدام مكتبات تابعة لجهات خارجية (هذا لا يعني أنه لا يوجد أي منها). لذا حان الوقت لتمتد أصابعك!
أنا في انتظار القارئ الذي يريد أن يفهم عمل خوارزميات الاستكشاف ، وكذلك الخبراء في الخوارزميات للتعرف على التنفيذ وطرق تحسينها.
هيا بنا نبدأ!
رحلة في التاريخ
يمكن تمثيل شبكة ثنائية الأبعاد كرسم بياني ، حيث يكون لكل رأس 8 حواف:
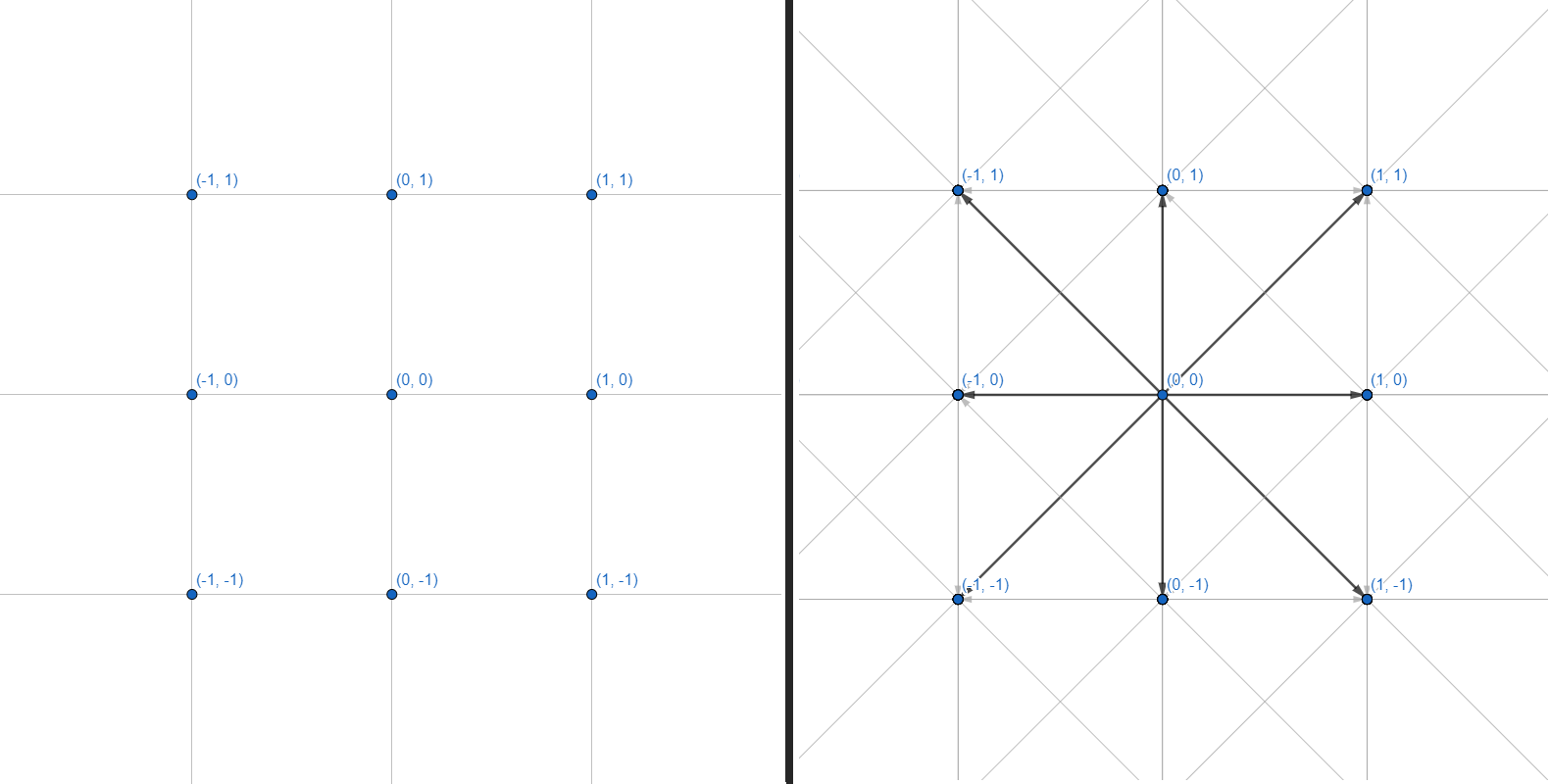
سنعمل مع الرسوم البيانية. كل رأس هو إحداثي عدد صحيح. كل حافة هي انتقال مستقيم أو قطري بين الإحداثيات المتجاورة. لن نقوم بشبكة الإحداثيات وحساب هندسة العوائق - سنقتصر على واجهة تقبل العديد من الإحداثيات كمدخلات وتعيد مجموعة من النقاط لبناء مسار:
public interface IPath
{
IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles);
}للبدء ، ضع في اعتبارك الطرق الحالية لاجتياز الرسم البياني.
بحث العمق
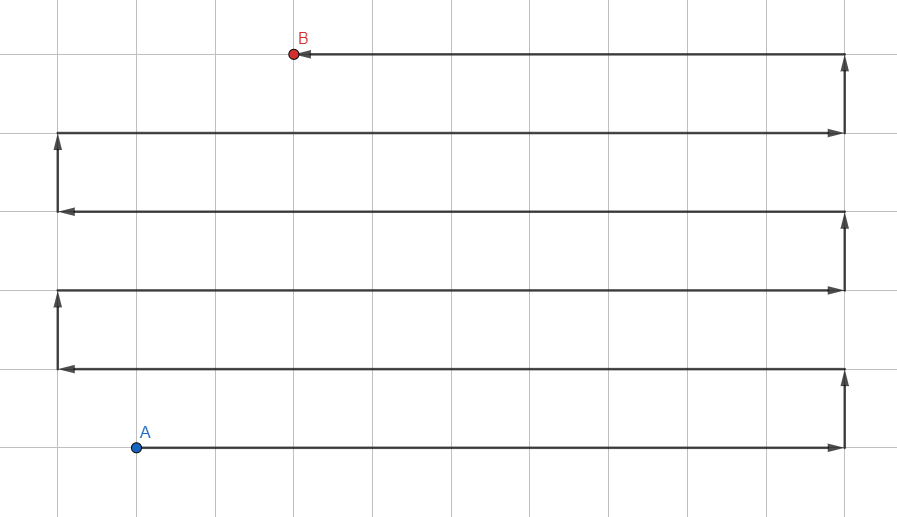
أبسط الخوارزميات:
- أضف جميع الرؤوس غير المرئية بالقرب من الحالي إلى المكدس.
- الانتقال إلى القمة الأولى من المكدس.
- إذا كان الرأس هو المطلوب ، اخرج من الدورة. إذا وصلت إلى طريق مسدود ، عد.
- اذهب 1.
تبدو هكذا:
, Node , .
private Node DFS(Node first, Node target)
{
List<Node> visited = new List<Node>();
Stack<Node> frontier = new Stack<Node>();
frontier.Push(first);
while (frontier.Count > 0)
{
var current = frontier.Pop();
visited.Add(current);
if (current == target)
return Node;
var neighbours = current.GenerateNeighbours();
foreach(var neighbour in neighbours)
if (!visited.Contains(neighbour))
frontier.Push(neighbour);
}
return default;
}, Node , .
يتم تنظيمه بتنسيق LIFO ( آخر ما يدخل - يخرج أولاً ) ، حيث يتم تحليل الرؤوس المضافة حديثًا أولاً. يجب مراقبة كل انتقال بين الرؤوس من أجل بناء المسار الفعلي على طول التحولات.
لن يؤدي هذا النهج أبدًا (تقريبًا) إلى إرجاع أقصر مسار لأنه يعالج الرسم البياني في اتجاه عشوائي. إنه أكثر ملاءمة للرسوم البيانية الصغيرة من أجل تحديد ما إذا كان هناك على الأقل بعض المسار إلى الرأس المطلوب (على سبيل المثال ، ما إذا كان الرابط المطلوب موجودًا في شجرة التكنولوجيا).
في حالة شبكة الملاحة والرسوم البيانية اللانهائية ، سيذهب هذا البحث إلى ما لا نهاية في اتجاه واحد ويضيع موارد الحوسبة ، ولن يصل أبدًا إلى النقطة المطلوبة. يتم حل ذلك عن طريق الحد من المنطقة التي تعمل فيها الخوارزمية. نجعله يحلل فقط النقاط التي لا تبعد أكثر من N من الخطوة الأولى. وهكذا ، عندما تصل الخوارزمية إلى حدود المنطقة ، فإنها تتكشف وتستمر في تحليل القمم داخل نصف القطر المحدد.
في بعض الأحيان يكون من المستحيل تحديد المنطقة بدقة ، لكنك لا تريد تعيين الحدود بشكل عشوائي. يأتي البحث المتعمق الأول للإنقاذ :
- قم بتعيين الحد الأدنى لمنطقة DFS.
- ابدأ البحث.
- إذا لم يتم العثور على المسار ، فقم بزيادة منطقة البحث بمقدار 1.
- اذهب 2.
سيتم تشغيل الخوارزمية مرارًا وتكرارًا ، وفي كل مرة تغطي مساحة أكبر حتى تجد النقطة المطلوبة في النهاية.
قد يبدو إعادة تشغيل الخوارزمية في نصف قطر أكبر قليلاً مضيعة للطاقة (على أي حال ، تم بالفعل تحليل معظم المنطقة في التكرار الأخير!) ، لكن لا: عدد الانتقالات بين الرؤوس ينمو هندسيًا مع كل زيادة في نصف القطر. إن أخذ نصف قطر أكبر مما تحتاج إليه سيكون أكثر تكلفة بكثير من المشي عدة مرات على طول أنصاف أقطار صغيرة.
من السهل لمثل هذا البحث تشديد حد المؤقت: سيبحث عن مسار بنصف قطر موسع تمامًا حتى ينتهي الوقت المحدد.
اتساع البحث الأول
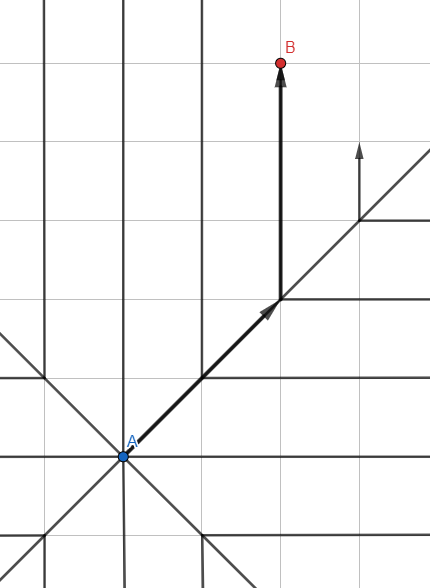
قد يشبه الرسم التوضيحي Jump Search - ولكن هذه هي خوارزمية الموجة المعتادة ، وتمثل الخطوط مسارات انتشار البحث مع إزالة النقاط الوسيطة.
على عكس البحث في العمق أولاً باستخدام مكدس (LIFO) ، فلنأخذ قائمة انتظار (FIFO) لمعالجة القمم:
- أضف جميع الجيران الذين لم تتم زيارتها إلى قائمة الانتظار.
- انتقل إلى الرأس الأول من قائمة الانتظار.
- إذا كان الرأس هو المطلوب ، فاخرج من الدورة ، وإلا فانتقل إلى 1.
تبدو هكذا:
, Node , .
private Node BFS(Node first, Node target)
{
List<Node> visited = new List<Node>();
Queue<Node> frontier = new Queue<Node>();
frontier.Enqueue(first);
while (frontier.Count > 0)
{
var current = frontier.Dequeue();
visited.Add(current);
if (current == target)
return Node;
var neighbours = current.GenerateNeighbours();
foreach(var neighbour in neighbours)
if (!visited.Contains(neighbour))
frontier.Enqueue(neighbour);
}
return default;
}, Node , .
يعطي هذا النهج المسار الأمثل ، ولكن هناك مشكلة: نظرًا لأن الخوارزمية تعالج الرؤوس في جميع الاتجاهات ، فإنها تعمل ببطء شديد على مسافات طويلة ورسوم بيانية ذات تفرع قوي. هذه هي حالتنا فقط.
هنا ، لا يمكن تحديد منطقة تشغيل الخوارزمية ، لأنها في أي حال لن تتجاوز نصف القطر إلى النقطة المطلوبة. طرق التحسين الأخرى مطلوبة.
أ *
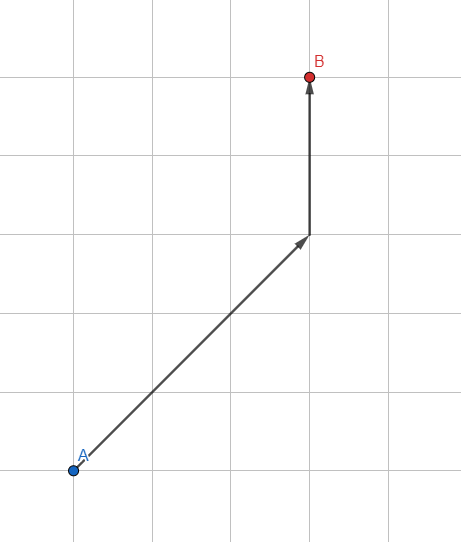
دعنا نعدل البحث القياسي ذي العرض الأول: نحن لا نستخدم قائمة انتظار منتظمة لتخزين الرؤوس ، لكننا نستخدم قائمة انتظار مرتبة بناءً على الاستدلال - تقدير تقريبي للمسار المتوقع.
كيف تقدر المسار المتوقع؟ الأبسط هو طول المتجه من الرأس المعالج إلى النقطة المرغوبة. كلما كان المتجه أصغر ، زادت النقطة الواعدة وأصبحت أقرب إلى بداية قائمة الانتظار. ستعطي الخوارزمية الأولوية لتلك النقاط التي تقع في اتجاه الهدف.
وبالتالي ، سيستغرق كل تكرار داخل الخوارزمية وقتًا أطول قليلاً بسبب الحسابات الإضافية ، ولكن عن طريق تقليل عدد الرؤوس للتحليل (سيتم معالجة أكثرها واعدة فقط) ، نحقق زيادة هائلة في سرعة الخوارزمية.
ولكن لا يزال هناك الكثير من الرؤوس المعالجة. إن إيجاد طول المتجه عملية مكلفة تتضمن حساب الجذر التربيعي. لذلك ، سوف نستخدم عملية حسابية مبسطة للإرشاد.
لنقم بإنشاء متجه عدد صحيح:
public readonly struct Vector2Int : IEquatable<Vector2Int>
{
private static readonly double Sqr = Math.Sqrt(2);
public Vector2Int(int x, int y)
{
X = x;
Y = y;
}
public int X { get; }
public int Y { get; }
/// <summary>
/// Estimated path distance without obstacles.
/// </summary>
public double DistanceEstimate()
{
int linearSteps = Math.Abs(Math.Abs(Y) - Math.Abs(X));
int diagonalSteps = Math.Max(Math.Abs(Y), Math.Abs(X)) - linearSteps;
return linearSteps + Sqr * diagonalSteps;
}
public static Vector2Int operator +(Vector2Int a, Vector2Int b)
=> new Vector2Int(a.X + b.X, a.Y + b.Y);
public static Vector2Int operator -(Vector2Int a, Vector2Int b)
=> new Vector2Int(a.X - b.X, a.Y - b.Y);
public static bool operator ==(Vector2Int a, Vector2Int b)
=> a.X == b.X && a.Y == b.Y;
public static bool operator !=(Vector2Int a, Vector2Int b)
=> !(a == b);
public bool Equals(Vector2Int other)
=> X == other.X && Y == other.Y;
public override bool Equals(object obj)
{
if (!(obj is Vector2Int))
return false;
var other = (Vector2Int) obj;
return X == other.X && Y == other.Y;
}
public override int GetHashCode()
=> HashCode.Combine(X, Y);
public override string ToString()
=> $"({X}, {Y})";
}هيكل قياسي لتخزين زوج من الإحداثيات. هنا نرى الجذر التربيعي التخزين المؤقت بحيث يمكن حسابه مرة واحدة فقط. ستسمح لنا واجهة IEquatable بمقارنة المتجهات مع بعضها البعض دون الحاجة إلى ترجمة Vector2Int إلى كائن والعكس. سيؤدي ذلك إلى تسريع الخوارزمية بشكل كبير والتخلص من عمليات التخصيص غير الضرورية.
يتم استخدام DistanceEstimate () لتقدير المسافة التقريبية للهدف من خلال حساب عدد الانتقالات المستقيمة والقطرية. طريقة بديلة شائعة:
return Math.Max(Math.Abs(X), Math.Abs(Y))سيعمل هذا الخيار بشكل أسرع ، ولكن يتم تعويض ذلك بالدقة المنخفضة لتقدير المسافة القطرية.
الآن بعد أن أصبح لدينا أداة للعمل مع الإحداثيات ، فلنقم بإنشاء كائن يمثل الجزء العلوي من الرسم البياني:
internal class PathNode
{
public PathNode(Vector2Int position, double traverseDist, double heuristicDist, PathNode parent)
{
Position = position;
TraverseDistance = traverseDist;
Parent = parent;
EstimatedTotalCost = TraverseDistance + heuristicDist;
}
public Vector2Int Position { get; }
public double TraverseDistance { get; }
public double EstimatedTotalCost { get; }
public PathNode Parent { get; }
}في Parent ، سنقوم بتسجيل الرأس السابق لكل رأس جديد: سيساعد ذلك في بناء المسار النهائي بالنقاط. بالإضافة إلى الإحداثيات ، نحفظ أيضًا المسافة المقطوعة والتكلفة المقدرة للمسار حتى نتمكن بعد ذلك من تحديد القمم الواعدة للمعالجة.
يطالب هذا الفصل بالتحسين ، لكننا سنعود إليه لاحقًا. في الوقت الحالي ، دعنا نطور طريقة تولد جيران الرأس:
internal static class NodeExtensions
{
private static readonly (Vector2Int position, double cost)[] NeighboursTemplate = {
(new Vector2Int(1, 0), 1),
(new Vector2Int(0, 1), 1),
(new Vector2Int(-1, 0), 1),
(new Vector2Int(0, -1), 1),
(new Vector2Int(1, 1), Math.Sqrt(2)),
(new Vector2Int(1, -1), Math.Sqrt(2)),
(new Vector2Int(-1, 1), Math.Sqrt(2)),
(new Vector2Int(-1, -1), Math.Sqrt(2))
};
public static IEnumerable<PathNode> GenerateNeighbours(this PathNode parent, Vector2Int target)
{
foreach ((Vector2Int position, double cost) in NeighboursTemplate)
{
Vector2Int nodePosition = position + parent.Position;
double traverseDistance = parent.TraverseDistance + cost;
double heuristicDistance = (position - target).DistanceEstimate();
yield return new PathNode(nodePosition, traverseDistance, heuristicDistance, parent);
}
}
}NeighboursTemplate - قالب محدد مسبقًا لإنشاء جيران خطي وقطري للنقطة المطلوبة. كما يأخذ في الاعتبار التكلفة المتزايدة للتحولات القطرية.
GenerateNeighbours - مولد يجتاز قالب الجيران ويعيد قمة جديدة لجميع الجوانب الثمانية المجاورة.
سيكون من الممكن دفع الوظيفة داخل PathNode ، لكن يبدو الأمر وكأنه انتهاك بسيط لـ SRP. ولا أرغب في إضافة وظائف الطرف الثالث داخل الخوارزمية نفسها أيضًا: سنحافظ على الطبقات مضغوطة قدر الإمكان.
حان الوقت للتعامل مع الفصل الدراسي الرئيسي!
public class Path
{
private readonly List<PathNode> frontier = new List<PathNode>();
private readonly List<Vector2Int> ignoredPositions = new List<Vector2Int>();
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles) {...}
private bool GenerateNodes(Vector2Int start, Vector2Int target,
IEnumerable<Vector2Int> obstacles, out PathNode node)
{
frontier.Clear();
ignoredPositions.Clear();
ignoredPositions.AddRange(obstacles);
// Add starting point.
frontier.Add(new PathNode(start, 0, 0, null));
while (frontier.Any())
{
// Find node with lowest estimated cost.
var lowest = frontier.Min(a => a.EstimatedTotalCost);
PathNode current = frontier.First(a => a.EstimatedTotalCost == lowest);
ignoredPositions.Add(current.Position);
if (current.Position.Equals(target))
{
node = current;
return true;
}
GenerateFrontierNodes(current, target);
}
// All nodes analyzed - no path detected.
node = null;
return false;
}
private void GenerateFrontierNodes(PathNode parent, Vector2Int target)
{
foreach (PathNode newNode in parent.GenerateNeighbours(target))
{
// Position is already checked or occupied by an obstacle.
if (ignoredPositions.Contains(newNode.Position)) continue;
// Node is not present in queue.
var node = frontier.FirstOrDefault(a => a.Position == newNode.Position);
if (node == null)
frontier.Add(newNode);
// Node is present in queue and new optimal path is detected.
else if (newNode.TraverseDistance < node.TraverseDistance)
{
frontier.Remove(node);
frontier.Add(newNode);
}
}
}
}يعمل GenerateNodes مع مجموعتين: الحدود ، والتي تحتوي على قائمة انتظار من الرؤوس للتحليل ، والمواضع المتجاهلة ، والتي تمت إضافة الرؤوس التي تمت معالجتها بالفعل.
يعثر كل تكرار للحلقة على قمة الرأس الواعدة ، ويتحقق مما إذا كنا قد وصلنا إلى نقطة النهاية ، ويولد جيرانًا جددًا لهذه القمة.
وكل هذا الجمال يتناسب مع 50 سطرًا.
يبقى تنفيذ الواجهة:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles)
{
if (!GenerateNodes(start, target, obstacles, out PathNode node))
return Array.Empty<Vector2Int>();
var output = new List<Vector2Int>();
while (node.Parent != null)
{
output.Add(node.Position);
node = node.Parent;
}
output.Add(start);
return output.AsReadOnly();
}يعيد GenerateNodes لنا الرأس الأخير ، وبما أننا كتبنا جارًا رئيسيًا لكل واحد منهم ، يكفي المرور عبر جميع الآباء حتى القمة الأولية ، وسنحصل على أقصر طريق. كل شيء على ما يرام!
أم لا؟
تحسين الخوارزمية
1. PathNode
لنبدأ ببساطة. لنبسط PathNode:
internal readonly struct PathNode
{
public PathNode(Vector2Int position, Vector2Int target, double traverseDistance)
{
Position = position;
TraverseDistance = traverseDistance;
double heuristicDistance = (position - target).DistanceEstimate();
EstimatedTotalCost = traverseDistance + heuristicDistance;
}
public Vector2Int Position { get; }
public double TraverseDistance { get; }
public double EstimatedTotalCost { get; }
}هذا هو غلاف بيانات شائع يتم إنشاؤه في كثير من الأحيان. لا يوجد سبب لجعلها فئة وتحميل ذاكرة في كل مرة نكتب فيها جديدة . لذلك ، سوف نستخدم الهيكل.
ولكن هناك مشكلة: لا يمكن للبنى أن تحتوي على مراجع دائرية لنوعها الخاص. لذلك ، بدلاً من تخزين العنصر الرئيسي داخل PathNode ، نحتاج إلى طريقة أخرى لتتبع بناء المسارات بين الرؤوس. الأمر سهل - دعنا نضيف مجموعة جديدة إلى فئة Path:
private readonly Dictionary<Vector2Int, Vector2Int> links;ونقوم بتعديل طفيف على جيل الجيران:
private void GenerateFrontierNodes(PathNode parent, Vector2Int target)
{
foreach (PathNode newNode in parent.GenerateNeighbours(target))
{
// Position is already checked or occupied by an obstacle.
if (ignoredPositions.Contains(newNode.Position)) continue;
// Node is not present in queue.
if (!frontier.TryGet(newNode.Position, out PathNode existingNode))
{
frontier.Enqueue(newNode);
links[newNode.Position] = parent.Position; // Add link to dictionary.
}
// Node is present in queue and new optimal path is detected.
else if (newNode.TraverseDistance < existingNode.TraverseDistance)
{
frontier.Modify(newNode);
links[newNode.Position] = parent.Position; // Add link to dictionary.
}
}
}بدلاً من كتابة الأصل إلى الرأس نفسه ، نكتب الانتقال إلى القاموس. كمكافأة ، يمكن أن يعمل القاموس مباشرة مع Vector2Int ، وليس مع PathNode ، لأننا نحتاج فقط إلى الإحداثيات ولا شيء آخر.
إنشاء النتيجة داخل الحساب مبسط أيضًا:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles)
{
if (!GenerateNodes(start, target, obstacles))
return Array.Empty<Vector2Int>();
var output = new List<Vector2Int> {target};
while (links.TryGetValue(target, out target))
output.Add(target);
return output.AsReadOnly();
}2. NodeExtensions
بعد ذلك ، دعونا نتعامل مع جيل الجيران. I لا تعد ولا تحصى ، على الرغم من كل فوائدها ، فإنها تولد كمية حزينة من القمامة في كثير من المواقف. دعنا نتخلص منه:
internal static class NodeExtensions
{
private static readonly (Vector2Int position, double cost)[] NeighboursTemplate = {
(new Vector2Int(1, 0), 1),
(new Vector2Int(0, 1), 1),
(new Vector2Int(-1, 0), 1),
(new Vector2Int(0, -1), 1),
(new Vector2Int(1, 1), Math.Sqrt(2)),
(new Vector2Int(1, -1), Math.Sqrt(2)),
(new Vector2Int(-1, 1), Math.Sqrt(2)),
(new Vector2Int(-1, -1), Math.Sqrt(2))
};
public static void Fill(this PathNode[] buffer, PathNode parent, Vector2Int target)
{
int i = 0;
foreach ((Vector2Int position, double cost) in NeighboursTemplate)
{
Vector2Int nodePosition = position + parent.Position;
double traverseDistance = parent.TraverseDistance + cost;
buffer[i++] = new PathNode(nodePosition, target, traverseDistance);
}
}
}الآن طريقة الامتداد الخاصة بنا ليست منشئًا: إنها تملأ المخزن المؤقت الذي يتم تمريره إليه كوسيطة. يتم تخزين المخزن المؤقت كمجموعة أخرى داخل المسار:
private const int MaxNeighbours = 8;
private readonly PathNode[] neighbours = new PathNode[MaxNeighbours];ويتم استخدامه على النحو التالي:
neighbours.Fill(parent, target);
foreach(var neighbour in neighbours)
{
// ...3. HashSet
بدلاً من استخدام القائمة ، دعنا نستخدم HashSet:
private readonly HashSet<Vector2Int> ignoredPositions;إنها أكثر فاعلية عند العمل مع مجموعات كبيرة ، والطريقة المتجاهلة Positions.Contains () تستهلك الكثير من الموارد بسبب تكرار المكالمات. سيؤدي التغيير البسيط في نوع المجموعة إلى تعزيز أداء ملحوظ.
4. BinaryHeap
هناك مكان واحد في تطبيقنا يؤدي إلى إبطاء الخوارزمية عشرة أضعاف:
// Find node with lowest estimated cost.
var lowest = frontier.Min(a => a.EstimatedTotalCost);
PathNode current = frontier.First(a => a.EstimatedTotalCost == lowest);القائمة نفسها هي اختيار سيئ ، واستخدام Linq يجعل الأمور أسوأ.
من الناحية المثالية ، نريد مجموعة بها:
- الفرز التلقائي.
- انخفاض نمو التعقيد المقارب.
- عملية إدخال سريعة.
- عملية إزالة سريعة.
- سهولة التنقل بين العناصر.
قد يبدو SortedSet كخيار جيد ، لكنه لا يعرف كيفية احتواء التكرارات. إذا كتبنا الفرز حسب EstimatedTotalCost ، فسيتم حذف كل النقاط التي لها نفس السعر (لكن بإحداثيات مختلفة!). في المناطق المفتوحة مع عدد قليل من العوائق ، هذا ليس مخيفًا ، بالإضافة إلى أنه سيؤدي إلى تسريع الخوارزمية ، ولكن في متاهات ضيقة ، ستكون النتيجة طرقًا غير دقيقة ونتائج سلبية خاطئة.
لذلك سنقوم بتنفيذ مجموعتنا - الكومة الثنائية ! يلبي التنفيذ الكلاسيكي 4 من أصل 5 متطلبات ، وتعديل صغير سيجعل هذه المجموعة مثالية لحالتنا.
المجموعة عبارة عن شجرة تم فرزها جزئيًا ، مع تعقيد عمليات الإدراج والحذف تساوي log (n) .
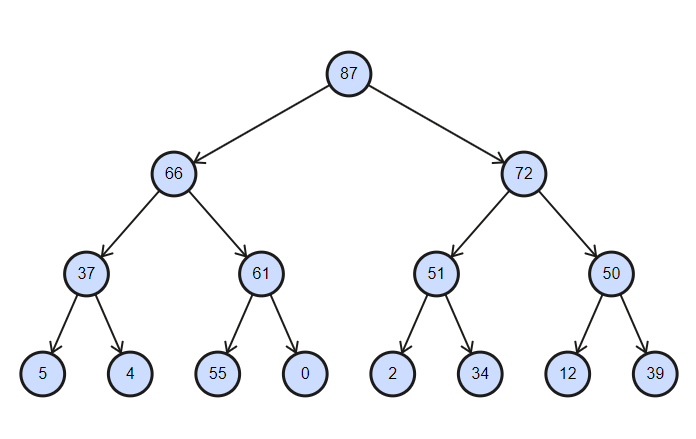
كومة ثنائية مرتبة بترتيب تنازلي
internal interface IBinaryHeap<in TKey, T>
{
void Enqueue(T item);
T Dequeue();
void Clear();
bool TryGet(TKey key, out T value);
void Modify(T value);
int Count { get; }
}لنكتب الجزء السهل:
internal class BinaryHeap : IBinaryHeap<Vector2Int, PathNode>
{
private readonly IDictionary<Vector2Int, int> map;
private readonly IList<PathNode> collection;
private readonly IComparer<PathNode> comparer;
public BinaryHeap(IComparer<PathNode> comparer)
{
this.comparer = comparer;
collection = new List<PathNode>();
map = new Dictionary<Vector2Int, int>();
}
public int Count => collection.Count;
public void Clear()
{
collection.Clear();
map.Clear();
}
// ...
}سوف نستخدم IComparer لفرز القمم المخصصة. IList هو في الواقع متجر قمة الرأس الذي سنعمل معه. نحتاج إلى IDictionary لتتبع مؤشرات القمم لإزالتها بسرعة (يتيح لنا التنفيذ القياسي للكومة الثنائية العمل بسهولة مع العنصر العلوي فقط).
دعنا نضيف عنصرًا:
public void Enqueue(PathNode item)
{
collection.Add(item);
int i = collection.Count - 1;
map[item.Position] = i;
// Sort nodes from bottom to top.
while(i > 0)
{
int j = (i - 1) / 2;
if (comparer.Compare(collection[i], collection[j]) <= 0)
break;
Swap(i, j);
i = j;
}
}
private void Swap(int i, int j)
{
PathNode temp = collection[i];
collection[i] = collection[j];
collection[j] = temp;
map[collection[i].Position] = i;
map[collection[j].Position] = j;
}تتم إضافة كل عنصر جديد إلى الخلية الأخيرة من الشجرة ، وبعد ذلك يتم فرزها جزئيًا من أسفل إلى أعلى: بواسطة العقد من العنصر الجديد إلى الجذر ، حتى يصل أصغر عنصر إلى أعلى مستوى ممكن. نظرًا لأنه لا يتم فرز المجموعة بأكملها ، ولكن فقط العقد الوسيطة بين القمة والأخيرة ، فإن العملية لها سجل التعقيد (n) .
الحصول على عنصر:
public PathNode Dequeue()
{
if (collection.Count == 0) return default;
PathNode result = collection.First();
RemoveRoot();
map.Remove(result.Position);
return result;
}
private void RemoveRoot()
{
collection[0] = collection.Last();
map[collection[0].Position] = 0;
collection.RemoveAt(collection.Count - 1);
// Sort nodes from top to bottom.
var i = 0;
while(true)
{
int largest = LargestIndex(i);
if (largest == i)
return;
Swap(i, largest);
i = largest;
}
}
private int LargestIndex(int i)
{
int leftInd = 2 * i + 1;
int rightInd = 2 * i + 2;
int largest = i;
if (leftInd < collection.Count
&& comparer.Compare(collection[leftInd], collection[largest]) > 0)
largest = leftInd;
if (rightInd < collection.Count
&& comparer.Compare(collection[rightInd], collection[largest]) > 0)
largest = rightInd;
return largest;
}قياسا على الإضافة: تتم إزالة الجذر ، ويتم وضع العنصر الأخير في مكانه. ثم يقوم الفرز الجزئي من أعلى لأسفل بتبديل العناصر بحيث يكون أصغرها في الأعلى.
بعد ذلك ننفذ البحث عن عنصر ونقوم بتغييره:
public bool TryGet(Vector2Int key, out PathNode value)
{
if (!map.TryGetValue(key, out int index))
{
value = default;
return false;
}
value = collection[index];
return true;
}
public void Modify(PathNode value)
{
if (!map.TryGetValue(value.Position, out int index))
throw new KeyNotFoundException(nameof(value));
collection[index] = value;
}لا يوجد شيء معقد هنا: نحن نبحث عن فهرس العنصر من خلال القاموس ، وبعد ذلك نصل إليه مباشرة.
نسخة عامة من الكومة:
internal class BinaryHeap<TKey, T> : IBinaryHeap<TKey, T> where TKey : IEquatable<TKey>
{
private readonly IDictionary<TKey, int> map;
private readonly IList<T> collection;
private readonly IComparer<T> comparer;
private readonly Func<T, TKey> lookupFunc;
public BinaryHeap(IComparer<T> comparer, Func<T, TKey> lookupFunc, int capacity)
{
this.comparer = comparer;
this.lookupFunc = lookupFunc;
collection = new List<T>(capacity);
map = new Dictionary<TKey, int>(capacity);
}
public int Count => collection.Count;
public void Enqueue(T item)
{
collection.Add(item);
int i = collection.Count - 1;
map[lookupFunc(item)] = i;
while(i > 0)
{
int j = (i - 1) / 2;
if (comparer.Compare(collection[i], collection[j]) <= 0)
break;
Swap(i, j);
i = j;
}
}
public T Dequeue()
{
if (collection.Count == 0) return default;
T result = collection.First();
RemoveRoot();
map.Remove(lookupFunc(result));
return result;
}
public void Clear()
{
collection.Clear();
map.Clear();
}
public bool TryGet(TKey key, out T value)
{
if (!map.TryGetValue(key, out int index))
{
value = default;
return false;
}
value = collection[index];
return true;
}
public void Modify(T value)
{
if (!map.TryGetValue(lookupFunc(value), out int index))
throw new KeyNotFoundException(nameof(value));
collection[index] = value;
}
private void RemoveRoot()
{
collection[0] = collection.Last();
map[lookupFunc(collection[0])] = 0;
collection.RemoveAt(collection.Count - 1);
var i = 0;
while(true)
{
int largest = LargestIndex(i);
if (largest == i)
return;
Swap(i, largest);
i = largest;
}
}
private void Swap(int i, int j)
{
T temp = collection[i];
collection[i] = collection[j];
collection[j] = temp;
map[lookupFunc(collection[i])] = i;
map[lookupFunc(collection[j])] = j;
}
private int LargestIndex(int i)
{
int leftInd = 2 * i + 1;
int rightInd = 2 * i + 2;
int largest = i;
if (leftInd < collection.Count && comparer.Compare(collection[leftInd], collection[largest]) > 0) largest = leftInd;
if (rightInd < collection.Count && comparer.Compare(collection[rightInd], collection[largest]) > 0) largest = rightInd;
return largest;
}
}الآن لدينا سرعة لائقة ، ولم يتبق أي جيل من القمامة. النهاية قريبة!
5. مجموعات قابلة لإعادة الاستخدام
يتم تطوير الخوارزمية مع مراعاة القدرة على تسميتها عشرات المرات في الثانية. إن إنشاء أي قمامة أمر غير مقبول بشكل قاطع: يمكن لمجمع القمامة المثقل (وسوف!) التسبب في تراجع دوري في الأداء
يتم الإعلان عن جميع المجموعات ، باستثناء المخرجات ، مرة واحدة بالفعل عند إنشاء الفئة ، ويتم إضافة المجموعة الأخيرة أيضًا هناك:
private const int MaxNeighbours = 8;
private readonly PathNode[] neighbours = new PathNode[MaxNeighbours];
private readonly IBinaryHeap<Vector2Int, PathNode> frontier;
private readonly HashSet<Vector2Int> ignoredPositions;
private readonly IList<Vector2Int> output;
private readonly IDictionary<Vector2Int, Vector2Int> links;
public Path()
{
var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost));
frontier = new BinaryHeap(comparer);
ignoredPositions = new HashSet<Vector2Int>();
output = new List<Vector2Int>();
links = new Dictionary<Vector2Int, Vector2Int>();
}تأخذ الطريقة العامة الشكل التالي:
public IReadOnlyCollection<Vector2Int> Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles)
{
if (!GenerateNodes(start, target, obstacles))
return Array.Empty<Vector2Int>();
output.Clear();
output.Add(target);
while (links.TryGetValue(target, out target))
output.Add(target);
return output.AsReadOnly();
}ولا يتعلق الأمر فقط بإنشاء مجموعات! تغير المجموعات سعتها ديناميكيًا عند ملؤها ، إذا كان المسار طويلًا ، فسيحدث تغيير الحجم عشرات المرات. هذا يستهلك الكثير من الذاكرة. عندما نقوم بمسح المجموعات وإعادة استخدامها دون الإعلان عن مجموعات جديدة ، فإنها تحتفظ بقدراتها. سيؤدي إنشاء المسار الأول إلى إنشاء الكثير من القمامة عند تهيئة المجموعات وتغيير قدراتها ، ولكن الاستدعاءات اللاحقة ستعمل بشكل جيد دون أي تخصيصات (بشرط أن يكون طول كل مسار محسوب زائدًا أو ناقصًا نفس الشيء بدون تشوهات حادة). ومن هنا النقطة التالية:
6. (مكافأة) إعلان عن حجم المجموعات
يطرح عدد من الأسئلة على الفور:
- هل من الأفضل تفريغ الحمولة إلى مُنشئ فئة Path ، أم تركها عند الاستدعاء الأول إلى pathfinder؟
- ما القدرة على تغذية المجموعات؟
- هل من الأرخص الإعلان عن سعة أكبر على الفور ، أم ترك المجموعة تتوسع من تلقاء نفسها؟
يمكن الإجابة على السؤال الثالث على الفور: إذا كان لدينا مئات وآلاف من الخلايا لإيجاد مسار ، فسيكون بالتأكيد أرخص تخصيص حجم معين لمجموعاتنا على الفور.
السؤالان الآخران يصعب الإجابة عليهما. يجب تحديد الإجابة على هذه الأسئلة بشكل تجريبي لكل حالة استخدام. إذا قررنا وضع الحمل في المُنشئ ، فقد حان الوقت لإضافة حد لعدد الخطوات إلى الخوارزمية الخاصة بنا:
public Path(int maxSteps)
{
this.maxSteps = maxSteps;
var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost));
frontier = new BinaryHeap(comparer, maxSteps);
ignoredPositions = new HashSet<Vector2Int>(maxSteps);
output = new List<Vector2Int>(maxSteps);
links = new Dictionary<Vector2Int, Vector2Int>(maxSteps);
}داخل GenerateNodes ، قم بتصحيح الحلقة:
var step = 0;
while (frontier.Count > 0 && step++ <= maxSteps)
{
// ...
}وهكذا ، يتم على الفور تخصيص سعة للمجموعات تساوي المسار الأقصى. لا تحتوي بعض المجموعات على العقد التي تم اجتيازها فحسب ، بل تحتوي أيضًا على جيرانها: بالنسبة لمثل هذه المجموعات ، يمكنك استخدام سعة أكبر من 4-5 مرات من المجموعة المحددة.
قد يبدو الأمر أكثر من اللازم ، ولكن بالنسبة للمسارات القريبة من الحد الأقصى المعلن ، فإن تخصيص حجم المجموعات يستهلك نصف إلى ثلاث مرات ذاكرة أقل من التوسع الديناميكي. من ناحية أخرى ، إذا قمت بتعيين قيم كبيرة جدًا لقيمة maxSteps وقمت بإنشاء مسارات قصيرة ، فإن مثل هذا الابتكار سيضر فقط. أوه ، ويجب ألا تحاول استخدام int.MaxValue!
سيكون الحل الأمثل هو إنشاء مُنشئين ، أحدهما يحدد السعة الأولية للمجموعات. ثم يمكن استخدام صفنا في كلتا الحالتين دون تعديله.
ماذا يمكنك أن تفعل أيضا؟
- .
- XML-.
- GetHashCode Vector2Int. , , , .
- , . .
- IComparable PathNode EqualityComparer. .
- : , . , , .
- قم بتغيير توقيع الطريقة في واجهتنا لتعكس جوهرها بشكل أفضل:
bool Calculate(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles, out IReadOnlyCollection<Vector2Int> path);
وهكذا ، تُظهر الطريقة بوضوح منطق عملها ، بينما كان يجب تسمية الطريقة الأصلية على النحو التالي: CalculateOrReturnEmpty .
الإصدار الأخير من فئة المسار:
/// <summary>
/// Reusable A* path finder.
/// </summary>
public class Path : IPath
{
private const int MaxNeighbours = 8;
private readonly PathNode[] neighbours = new PathNode[MaxNeighbours];
private readonly int maxSteps;
private readonly IBinaryHeap<Vector2Int, PathNode> frontier;
private readonly HashSet<Vector2Int> ignoredPositions;
private readonly List<Vector2Int> output;
private readonly IDictionary<Vector2Int, Vector2Int> links;
/// <summary>
/// Creation of new path finder.
/// </summary>
/// <exception cref="ArgumentOutOfRangeException"></exception>
public Path(int maxSteps = int.MaxValue, int initialCapacity = 0)
{
if (maxSteps <= 0)
throw new ArgumentOutOfRangeException(nameof(maxSteps));
if (initialCapacity < 0)
throw new ArgumentOutOfRangeException(nameof(initialCapacity));
this.maxSteps = maxSteps;
var comparer = Comparer<PathNode>.Create((a, b) => b.EstimatedTotalCost.CompareTo(a.EstimatedTotalCost));
frontier = new BinaryHeap<Vector2Int, PathNode>(comparer, a => a.Position, initialCapacity);
ignoredPositions = new HashSet<Vector2Int>(initialCapacity);
output = new List<Vector2Int>(initialCapacity);
links = new Dictionary<Vector2Int, Vector2Int>(initialCapacity);
}
/// <summary>
/// Calculate a new path between two points.
/// </summary>
/// <exception cref="ArgumentNullException"></exception>
public bool Calculate(Vector2Int start, Vector2Int target,
IReadOnlyCollection<Vector2Int> obstacles,
out IReadOnlyCollection<Vector2Int> path)
{
if (obstacles == null)
throw new ArgumentNullException(nameof(obstacles));
if (!GenerateNodes(start, target, obstacles))
{
path = Array.Empty<Vector2Int>();
return false;
}
output.Clear();
output.Add(target);
while (links.TryGetValue(target, out target)) output.Add(target);
path = output;
return true;
}
private bool GenerateNodes(Vector2Int start, Vector2Int target, IReadOnlyCollection<Vector2Int> obstacles)
{
frontier.Clear();
ignoredPositions.Clear();
links.Clear();
frontier.Enqueue(new PathNode(start, target, 0));
ignoredPositions.UnionWith(obstacles);
var step = 0;
while (frontier.Count > 0 && step++ <= maxSteps)
{
PathNode current = frontier.Dequeue();
ignoredPositions.Add(current.Position);
if (current.Position.Equals(target)) return true;
GenerateFrontierNodes(current, target);
}
// All nodes analyzed - no path detected.
return false;
}
private void GenerateFrontierNodes(PathNode parent, Vector2Int target)
{
neighbours.Fill(parent, target);
foreach (PathNode newNode in neighbours)
{
// Position is already checked or occupied by an obstacle.
if (ignoredPositions.Contains(newNode.Position)) continue;
// Node is not present in queue.
if (!frontier.TryGet(newNode.Position, out PathNode existingNode))
{
frontier.Enqueue(newNode);
links[newNode.Position] = parent.Position;
}
// Node is present in queue and new optimal path is detected.
else if (newNode.TraverseDistance < existingNode.TraverseDistance)
{
frontier.Modify(newNode);
links[newNode.Position] = parent.Position;
}
}
}
}رابط لشفرة المصدر