🤱🏽 🎚️ 🧜🏽 حرك كائنًا بالتساوي على طول منحنى 🤟🏿 🗾 🤺

في عملية تطوير لعبة في فئات أنواع مختلفة تمامًا ، قد يكون من الضروري "إطلاق" أي كائن لعبة على طول منحنى سلس بسرعة ثابتة أو مضبوطة ، سواء كانت شاحنة تتحرك من المدينة A إلى المدينة B ، أو صاروخًا يتم إطلاقه على طول مسار ماكر ، أو طائرة معادية القيام بمناورة على الأرض.

من المحتمل أن كل شخص مرتبط بالموضوع يعرف أو على الأقل سمع عن منحنيات بيزيير ، وخطوط B ، وشرائح هيرمايت وغيرها من شرائح الاستيفاء والتنعيم ، ويقترح بشكل صحيح تمامًا استخدام واحد منهم في الحالة الموصوفة ، ولكن ليس كل شيء بهذه البساطة كما نود.

في حالتنا ، الخدد هو وظيفة تعرض مجموعة من معلمات الإدخال (نقاط التحكم) وقيمة الوسيطة

t

$t$ (عادةً ما تأخذ القيم من 0 إلى 1) إلى نقطة على مستوى أو في الفضاء. المنحنى الناتج هو مجموعة قيم وظيفة الشريحة لـ

t \in [0, 1]

$t\in[0,1]$ ...

على سبيل المثال ، ضع في اعتبارك منحنى Bezier المكعب ، والذي يتم تقديمه بالمعادلة التالية:

$صورة$

منحنى بيزير المكعب

يوضح الشكل منحنيين بيزير مكعّبين ، محددين بأربع نقاط (يمر المنحنى من خلال اثنتين منهم ، والاثنان المتبقيان يحددان الانحناء). رسم متحرك

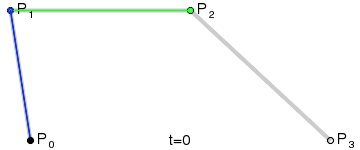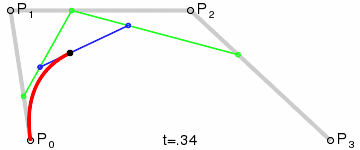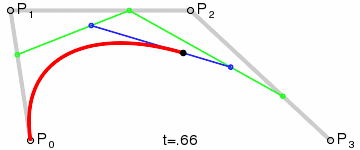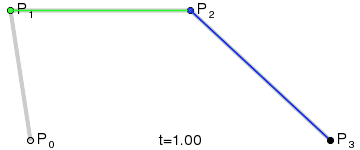
لعرض المعلمة t إلى نقطة منحنى من

أجل بناء مسار أكثر تعقيدًا ومتغيرًا من أقسام المنحنى ، يمكن توصيلها في سلسلة ، تاركًا نقطة ارتباط واحدة مشتركة:

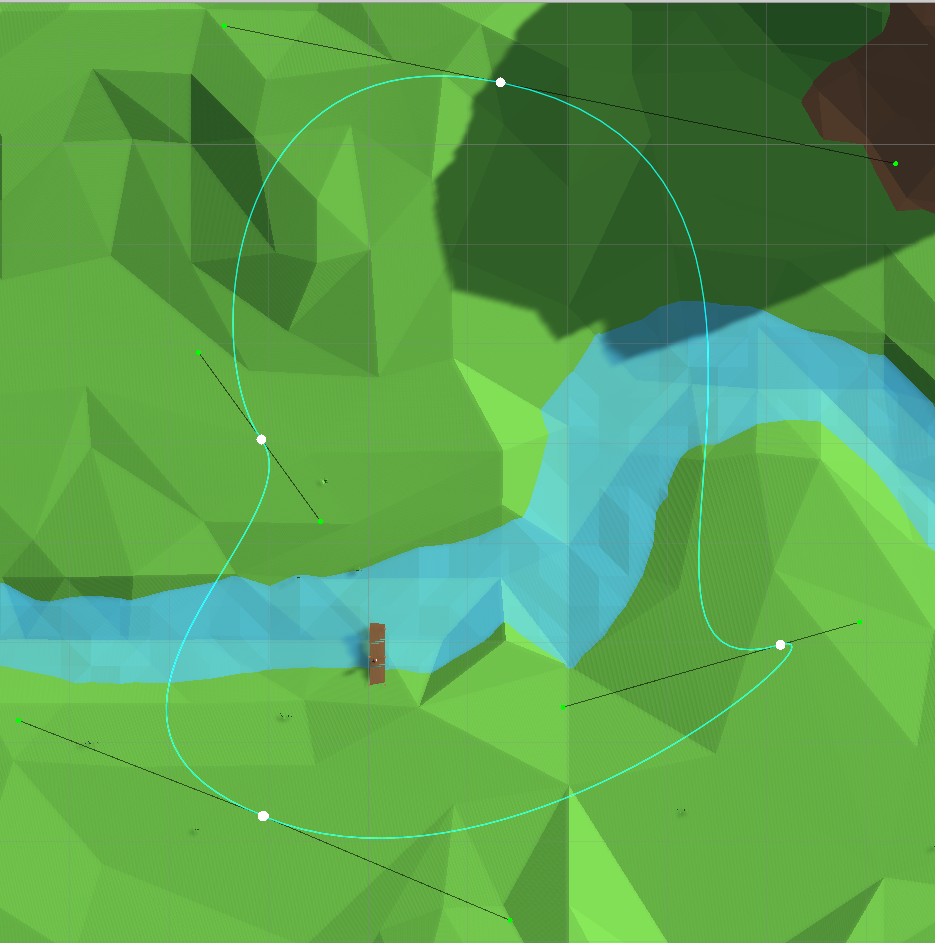
مخطط تفصيلي متقطع لقد اكتشفنا

المهمة وتحديد معايير المسار ، ننتقل الآن إلى السؤال الرئيسي. لكي يتحرك المستوى الشرطي على طول المسار بسرعة ثابتة ، نحتاج في أي وقت إلى أن نكون قادرين على حساب نقطة على المنحنى ، اعتمادًا على المسافة المقطوعة على طول هذا المنحنى.

s (l e n)

$s(len)$ ، مع القدرة فقط على حساب موضع نقطة على المنحنى من قيمة المعلمة

t

$t$ (وظيفة

y (t)

$y(t)$ ). في هذه المرحلة تبدأ الصعوبات.

كانت فكرتي الأولى هي القيام برسم خرائط خطية

l e n \in [0, L e n g t h] \Rightarrow t \in [0, 1]

$len\in[0, Length] \Rightarrow t\in[0,1]$ واحسب

y (t)

$y(t)$ من القيمة الناتجة - ما تحتاجه سهل ، ورخيص حسابيا ، بشكل عام.

مشكلة هذه الطريقة واضحة على الفور - في الواقع ، المسافة المقطوعة

s

$s$ يعتمد على

t

$t$ غير خطي ، ولكي تكون مقتنعًا بذلك ، يكفي الترتيب على طول المسار الموزع بشكل موحد حسب القيمة

t

$t$ النقاط: النقاط

"بالتساوي" موزعة على طول المسار

سوف تتباطأ الطائرة في بعض الأقسام وتتسارع في البعض الآخر ، مما يجعل طريقة تحديد معاملات المنحنى هذه غير قابلة للتطبيق تمامًا لحل المشكلة الموصوفة (تم اختيار الطائرة حصريًا كمثال توضيحي ولم يتم متابعة الهدف من وصف حركتها بطريقة صحيحة ماديًا ):

تصور معلمات غير صحيحة للمنحنى

بعد استشارة محرك البحث ، على stackoverflow و youtube ، وجدت طريقة ثانية لحساب

s (l e n) = g (t)

$s(len) = g(t)$ ، أي تمثيل المنحنى في شكل دالة متعددة الخطوط (حساب مجموعة من النقاط على مسافة متساوية من بعضها البعض على طول المنحنى):

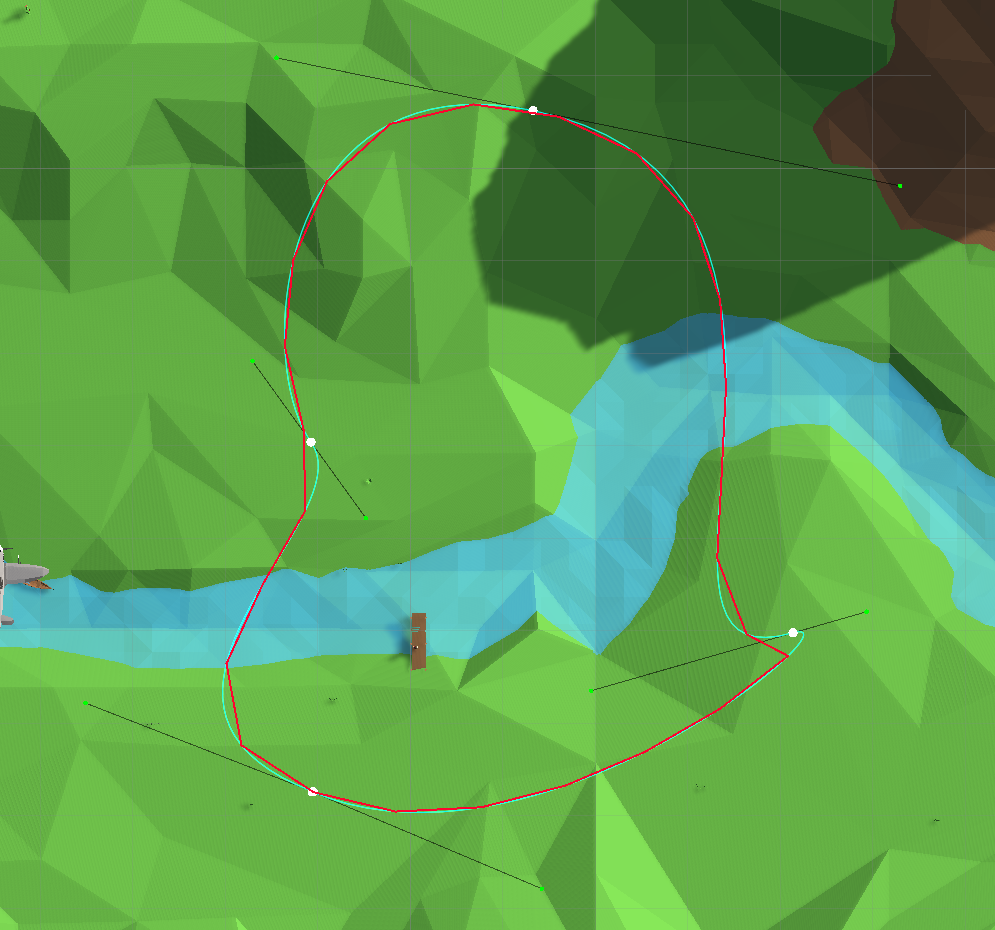
تمثيل المنحنى على شكل شريحة خطية متعددة الأجزاء

هذا الإجراء تكراري: يتم اتخاذ خطوة صغيرة

t

$t$ ، نتحرك على طول منحنى معها ، ونلخص المسافة المقطوعة بطول شريحة خطية متعددة الأجزاء حتى يتم تغطية مسافة معينة ، وبعد ذلك يتم تذكر النقطة ، وتستأنف العملية.

عينة من الرموز

مصدر

public Vector2[] CalculateEvenlySpacedPoints(float spacing, float resolution = 1)
  {
    List<Vector2> evenlySpacedPoints = new List<Vector2>();
    evenlySpacedPoints.Add(points[0]);
    Vector2 previousPoint = points[0];
    float dstSinceLastEvenPoint = 0;

    for (int segmentIndex = 0; segmentIndex < NumSegments; segmentIndex++)
    {
      Vector2[] p = GetPointsInSegment(segmentIndex);
      float controlNetLength = Vector2.Distance(p[0], p[1]) + Vector2.Distance(p[1], p[2]) + Vector2.Distance(p[2], p[3]);
      float estimatedCurveLength = Vector2.Distance(p[0], p[3]) + controlNetLength / 2f;
      int divisions = Mathf.CeilToInt(estimatedCurveLength * resolution * 10);
      float t = 0;
      while (t <= 1)
      {
        t += 1f/divisions;
        Vector2 pointOnCurve = Bezier.EvaluateCubic(p[0], p[1], p[2], p[3], t);
        dstSinceLastEvenPoint += Vector2.Distance(previousPoint, pointOnCurve);

        while (dstSinceLastEvenPoint >= spacing)
        {
          float overshootDst = dstSinceLastEvenPoint - spacing;
          Vector2 newEvenlySpacedPoint = pointOnCurve + (previousPoint - pointOnCurve).normalized * overshootDst;
          evenlySpacedPoints.Add(newEvenlySpacedPoint);
          dstSinceLastEvenPoint = overshootDst;
          previousPoint = newEvenlySpacedPoint;
        }

        previousPoint = pointOnCurve;
      }
    }

    return evenlySpacedPoints.ToArray();
  }

ويبدو أن المشكلة قد تم حلها ، لأنه يمكنك تقسيم المسار إلى العديد من المقاطع والاستمتاع بمدى سلاسة وقياس حركة الجسم ، نظرًا لأن حساب نقطة على دالة خطية متعددة التعابير يعد أمرًا بسيطًا وسريعًا. ولكن هذا النهج له أيضًا عيوب واضحة تزعجني - إجراء مكلف إلى حد ما لتغيير خطوة التقسيم أو هندسة المنحنى والحاجة إلى إيجاد توازن بين الدقة (المزيد من استهلاك الذاكرة) وتوفير الذاكرة (يصبح المسار "المكسور" أكثر وضوحًا).

ونتيجة لذلك ، واصلت البحث ووجدت مقالًا ممتازًا بعنوان "التحرك على طول منحنى بسرعة محددة" ، والذي يقوم على أساسه مزيد من التفكير.

يمكن حساب قيمة السرعة على أنها

σ (t) = | V (t) | = | \frac{d X}{d t} |

$\sigma(t) = |V(t)|=|\frac{dX}{dt}|$ أين

X (t)

$X(t)$ - وظيفة خدد. لحل المشكلة ، تحتاج إلى إيجاد الوظيفة

Y (t) = X (s)

$Y(t)=X(s)$ أين

s

$s$ - طول القوس من نقطة البداية إلى النقطة المرغوبة ، وهذا التعبير يؤسس العلاقة بينهما

t

$t$ و

s

$s$ ...

باستخدام تعويض متغير التفاضل ، يمكننا الكتابة

\frac{d Y}{d t} = \frac{d X}{d s} \frac{d s}{d t} .

$\frac{dY}{dt}=\frac{dX}{ds}\frac{ds}{dt}.$

مع الأخذ في الاعتبار أن السرعة كمية غير سالبة نحصل عليها

| \frac{d Y}{d t} | = | \frac{d X}{d s} | | \frac{d s}{d t} | = \frac{d s}{d t},

$|\frac{dY}{dt}|=|\frac{dX}{ds}||\frac{ds}{dt}|=\frac{ds}{dt},$

لان

| \frac{d X}{d s} | = 1

$|\frac{dX}{ds}| = 1$ بشرط أن يظل معامل متجه السرعة ثابتًا (بشكل عام ،

| \frac{d X}{d s} |

$|\frac{dX}{ds}|$ لا يساوي واحدًا ، بل ثابتًا ، ولكن لتبسيط العمليات الحسابية ، سنأخذ هذا الثابت يساوي واحدًا).

الآن نحصل على النسبة بين

t

$t$ و

s

$s$ صراحة:

s = g (t) = \int_{0}^{t} | \frac{d Y (τ)}{d t} | d τ,

$s=g(t)=\int_{0}^{t}|\frac{dY(\tau)}{dt}|d\tau,$

من أين الطول الكلي للمنحنى

L

$L$ من الواضح أنه محسوب على أنه

g (1)

$g(1)$ ... باستخدام الصيغة الناتجة ، من الممكن أن يكون لها قيمة الوسيطة

t

$t$ ، احسب طول القوس إلى النقطة التي تكون عندها هذه القيمة

t

$t$ معروض.

نحن مهتمون بالعملية العكسية ، أي حساب قيمة الوسيطة

t

$t$ على طول قوس معين

s

$s$ :

t = g^{- 1} (s) .

$t=g^{-1}(s).$

نظرًا لعدم وجود طريقة تحليلية عامة لإيجاد الدالة العكسية ، فسيتعين عليك البحث عن حل رقمي. نشير

F (t) = g (t) - s .

$F(t)=g(t)-s.$ لاجل منحه

s

$s$ ، لا بد من إيجاد مثل هذه القيمة

t

$t$ الذي

F (t) = 0

$F(t)=0$ ... وهكذا ، تحولت المهمة إلى مهمة إيجاد جذر المعادلة ، والتي يمكن لطريقة نيوتن التعامل معها تمامًا.

الطريقة تشكل تسلسل تقريبي للنموذج

t_{i + 1} = t_{i} - \frac{F (t_{i})}{F^{'} (t_{i})},

$t_{i+1}=t_i-\frac{F(t_i)}{F'(t_i)},$

أين

F^{'} (t) = \frac{d F}{d t} = \frac{d g}{d t} = | \frac{d Y}{d t} | .

$F'(t)=\frac{dF}{dt}=\frac{dg}{dt}=|\frac{dY}{dt}|.$

لكي يحسب

F (t)

$F(t)$ بحاجة لحساب

g (t)

$g(t)$ ، يتطلب حسابه بدوره تكاملًا عدديًا.

خيار

t_{0} = \frac{s}{L}

$t_0=\frac{s}{L}$ كتقريب أولي يبدو الآن معقولاً (تذكر الطريقة الأولى لحل المشكلة).

بعد ذلك ، نكرر استخدام طريقة نيوتن حتى يصبح خطأ الحل مقبولًا ، أو أن عدد التكرارات التي تم إجراؤها كبير للغاية.

هناك مشكلة محتملة في استخدام طريقة نيوتن القياسية. وظيفة

F (t)

$F(t)$ - غير متناقص منذ مشتقه

F^{'} (t) = | d Y / d t |

$F'(t)=|dY/dt|$ غير سالب. إذا كان المشتق الثاني

F^{″} (t) > 0

$F''(t)>0$ ، ثم تسمى الوظيفة محدبة وطريقة نيوتن مضمونة لتتقارب مع الجذر. ومع ذلك ، في حالتنا ،

F^{″} (t)

$F''(t)$ قد تكون سلبية ، بسبب طريقة نيوتن التي قد تتقارب خارج نطاق التعريف

t \in [0, 1]

$t\in[0,1]$ ... يقترح مؤلف المقال استخدام تعديل لطريقة نيوتن ، والتي ، إذا كانت نتيجة التكرار التالية بواسطة طريقة نيوتن لا تقع في الفاصل الزمني الحالي الذي يحيط بالجذر ، فإنه يختار بدلاً من ذلك منتصف الفترة ( طريقة الانقسام ). بغض النظر عن نتيجة الحساب عند التكرار الحالي ، يتم تضييق النطاق ، مما يعني أن الطريقة تتقارب مع الجذر.

يبقى اختيار طريقة التكامل العددي - لقد استخدمت تربيعات طريقة غاوس ، لأنها توفر نتيجة دقيقة إلى حد ما بتكلفة منخفضة.

رمز الوظيفة لحساب t (s)

public float ArcLength(float t) => Integrate(x => TangentMagnitude(x), 0, t);

private float Parameter(float length)
{
  float t = 0 + length / ArcLength(1);
  float lowerBound = 0f; 
  float upperBound = 1f;

  for (int i = 0; i < 100; ++i)
  {
    float f = ArcLength(t) - length;

    if (Mathf.Abs(f) < 0.01f)
      break;

    float derivative = TangentMagnitude(t);
    float candidateT = t - f / derivative;

    if (f > 0)
    {
      upperBound = t;
      if (candidateT <= 0)
        t = (upperBound + lowerBound) / 2;
      else
        t = candidateT;
    }
    else
    {
      lowerBound = t;
      if (candidateT >= 1)
        t = (upperBound + lowerBound) / 2;
      else
        t = candidateT;
    }
  }
  return t;
}

كود دالة التكامل العددي

private static readonly (float, float)[] CubicQuadrature =
{(-0.7745966F, 0.5555556F), (0, 0.8888889F), (0.7745966F, 0.5555556F)};

public static float Integrate(Func<float, float> f, in float lowerBound, in float uppedBound)
{
  var sum = 0f;
  foreach (var (arg, weight) in CubicQuadrature)
  {
    var t = Mathf.Lerp(lowerBound, uppedBound, Mathf.InverseLerp(-1, 1, arg));
    sum += weight * f(t);
  }

  return sum * (upperBound - lowerBound) / 2;
}

بعد ذلك ، يمكنك ضبط خطأ طريقة نيوتن ، واختيار طريقة أكثر دقة للتكامل العددي ، ولكن المشكلة ، في الواقع ، قد تم حلها - تم إنشاء خوارزمية لحساب الوسيطة

t

$t$ شريحة لطول قوس معين. لدمج عدة أقسام من المنحنيات في قسم واحد وكتابة إجراء حساب معمم

s (t)

$s(t)$ يمكنك تخزين أطوال جميع المقاطع والحساب المسبق لفهرس المقطع حيث تريد تنفيذ إجراء تكراري باستخدام طريقة نيوتن المعدلة.

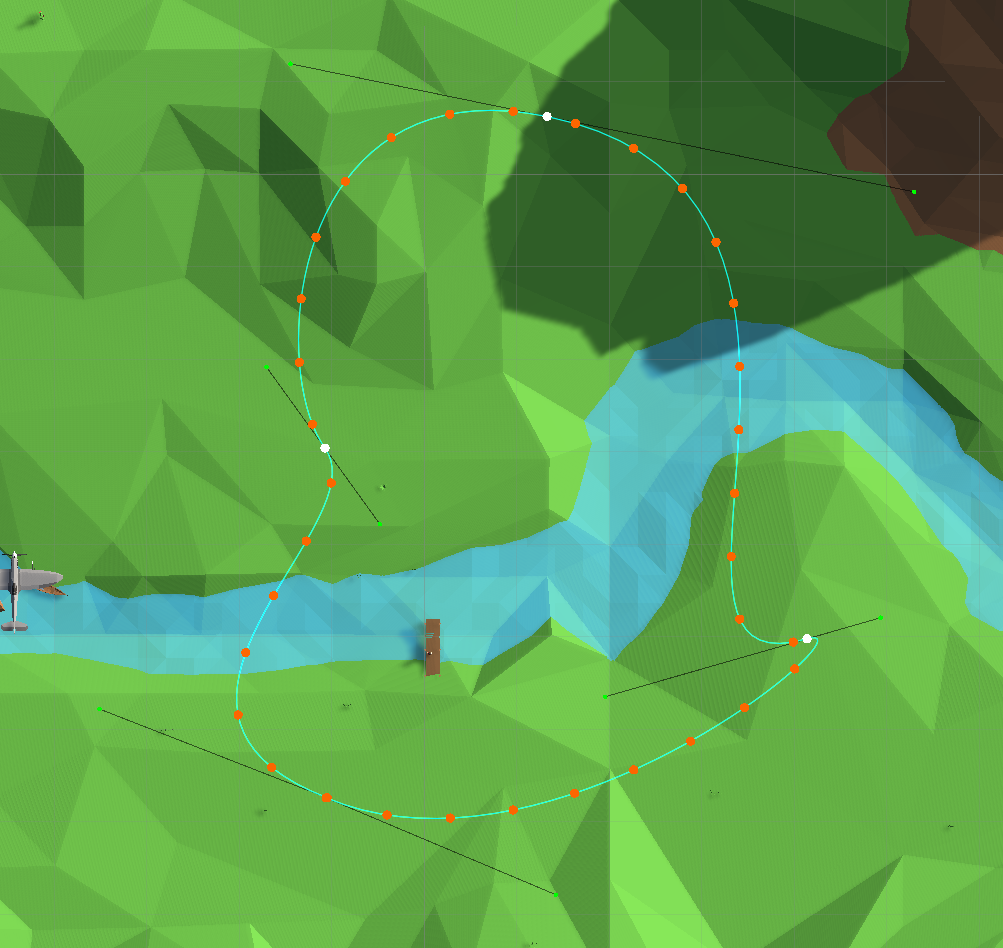
النقاط موزعة بالتساوي على طول المسار

الآن تتحرك الطائرة بشكل موحد

وهكذا ، فقد درسنا عدة طرق لتحديد معلمات الشريحة فيما يتعلق بالمسافة المقطوعة ، في المقالة التي استخدمتها كمصدر ، كخيار ، يقترح المؤلف حل المعادلة التفاضلية عدديًا ، ولكن وفقًا لملاحظته الخاصة ، يفضل الطريقة المعدلة نيوتن:

أنا أفضل طريقة نيوتن لأنه يمكن حساب t بشكل عام أسرع من حل المعادلات التفاضلية.

في الختام ، سأقدم جدولًا زمنيًا لحساب موضع نقطة على المنحنى الموضح في لقطات الشاشة في مؤشر ترابط واحد على معالج i5-9600K:

عدد العمليات الحسابية	متوسط الوقت ، مللي
100	0.62
1000	6.24
10000	69.01
100،000	672.81

أعتقد أن هذه السرعة في العمليات الحسابية تجعل من الممكن استخدامها في ألعاب ومحاكاة مختلفة. سأكون سعيدًا للتوضيح والانتقاد في الجوهر في التعليقات.

حرك كائنًا بالتساوي على طول منحنى

More articles: