المقدمة
تصف هذه المقالة خوارزمية فرز دمج تكيفية مستقرة غير متكررة تسمى quadsort.
التبادل الرباعي
كوادسورت مبني على تبادل رباعي. تقليديا ، تعتمد معظم خوارزميات الفرز على التبادل الثنائي ، حيث يتم فرز متغيرين باستخدام متغير مؤقت ثالث. عادة ما يبدو كالتالي:
if (val[0] > val[1])
{
tmp[0] = val[0];
val[0] = val[1];
val[1] = tmp[0];
}في التبادل الرباعي ، يحدث الفرز باستخدام أربعة متغيرات إحلال (مقايضة). في الخطوة الأولى ، يتم فرز المتغيرات الأربعة جزئيًا إلى أربعة متغيرات مبادلة ، في الخطوة الثانية ، يتم فرزها بالكامل مرة أخرى في المتغيرات الأربعة الأصلية.
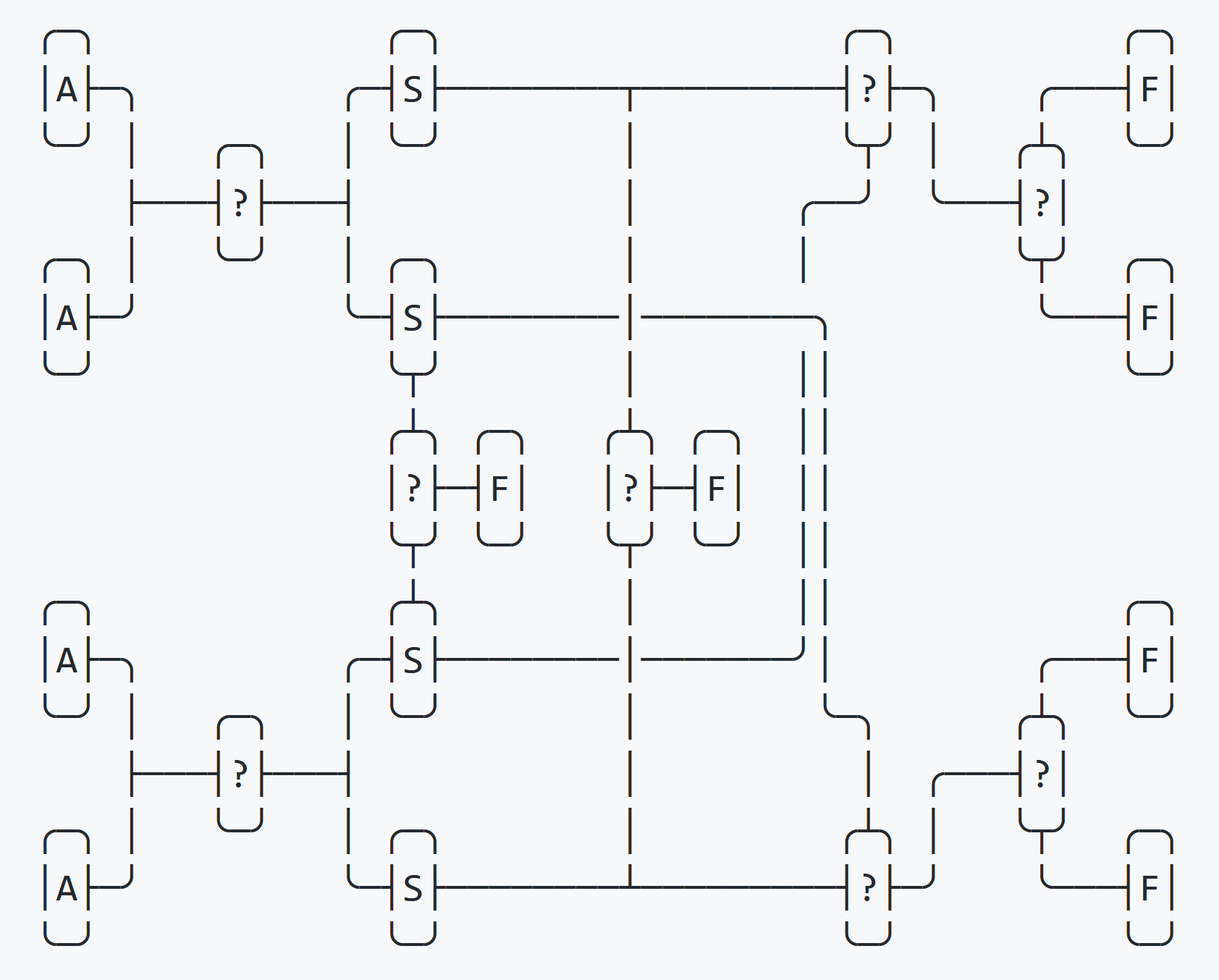
هذه العملية موضحة في الرسم البياني أعلاه.
بعد الجولة الأولى من الفرز ، يحدد واحد إذا كان الاختيار ما إذا كانت متغيرات المبادلة الأربعة مرتبة بالترتيب. إذا كان الأمر كذلك ، ينتهي التبادل على الفور. ثم يتحقق لمعرفة ما إذا كانت متغيرات المبادلة مرتبة بترتيب عكسي. إذا كان الأمر كذلك ، ينتهي الفرز على الفور. إذا فشل كلا الاختبارين ، فعندئذٍ يكون الموقع النهائي معروفًا ويبقى اختباران لتحديد الترتيب النهائي.
هذا يلغي مقارنة واحدة زائدة عن الحاجة للتسلسلات بالترتيب. في الوقت نفسه ، يتم إنشاء مقارنة إضافية واحدة للتسلسلات العشوائية. ومع ذلك ، في العالم الحقيقي ، نادرًا ما نقارن البيانات العشوائية الحقيقية. لذلك عندما يتم ترتيب البيانات بدلاً من الفوضى ، يكون هذا التحول في الاحتمال مفيدًا.
هناك أيضًا تحسن عام في الأداء بسبب التخلص من المبادلة المهدرة. في C ، تبدو المقايضة الرباعية الأساسية كما يلي:
if (val[0] > val[1])
{
tmp[0] = val[1];
tmp[1] = val[0];
}
else
{
tmp[0] = val[0];
tmp[1] = val[1];
}
if (val[2] > val[3])
{
tmp[2] = val[3];
tmp[3] = val[2];
}
else
{
tmp[2] = val[2];
tmp[3] = val[3];
}
if (tmp[1] <= tmp[2])
{
val[0] = tmp[0];
val[1] = tmp[1];
val[2] = tmp[2];
val[3] = tmp[3];
}
else if (tmp[0] > tmp[3])
{
val[0] = tmp[2];
val[1] = tmp[3];
val[2] = tmp[0];
val[3] = tmp[1];
}
else
{
if (tmp[0] <= tmp[2])
{
val[0] = tmp[0];
val[1] = tmp[2];
}
else
{
val[0] = tmp[2];
val[1] = tmp[0];
}
if (tmp[1] <= tmp[3])
{
val[2] = tmp[1];
val[3] = tmp[3];
}
else
{
val[2] = tmp[3];
val[3] = tmp[1];
}
}في حالة تعذر تقسيم المصفوفة بشكل مثالي إلى أربعة أجزاء ، يتم فرز الذيل المكون من 1-3 عناصر باستخدام التبادل الثنائي التقليدي.
يتم تنفيذ التبادل الرباعي الموصوف أعلاه في quadsort.
دمج رباعي
في المرحلة الأولى ، يقوم التبادل الرباعي بفرز المصفوفة مسبقًا إلى كتل من أربعة عناصر ، كما هو موضح أعلاه.
تستخدم المرحلة الثانية نهجًا مشابهًا لاكتشاف الأوامر المرتبة والمنعكسة ، ولكن في الكتل المكونة من 4 أو 16 أو 64 أو أكثر من العناصر ، يتم التعامل مع هذه المرحلة كفرز دمج تقليدي.
يمكن تمثيل ذلك على النحو التالي:
main memory: AAAA BBBB CCCC DDDD
swap memory: ABABABAB CDCDCDCD
main memory: ABCDABCDABCDABCDيستخدم السطر الأول مقايضة رباعية لإنشاء أربع كتل من أربعة عناصر مرتبة لكل منها. يستخدم السطر الثاني دمج رباعي للدمج في كتلتين من ثمانية عناصر مرتبة في ذاكرة المبادلة. في السطر الأخير ، يتم دمج الكتل مرة أخرى في الذاكرة الرئيسية ، ويتبقى لدينا كتلة واحدة من 16 عنصرًا مرتبة. أدناه هو التصور.

تتطلب هذه العمليات في الواقع مضاعفة ذاكرة المبادلة. المزيد عن هذا لاحقًا.
تخطى
يتمثل الاختلاف الآخر في أنه نظرًا لزيادة تكلفة عمليات الدمج ، من المفيد التحقق مما إذا كانت أربع كتل بترتيب أمامي أو عكسي.
في حالة ترتيب الكتل الأربعة ، يتم تخطي عملية الدمج ، لأنها لا معنى لها. ومع ذلك ، يتطلب هذا فحصًا إضافيًا ، وبالنسبة للبيانات المصنفة عشوائيًا ، هذا إذا أصبح الاختيار غير مرجح بشكل متزايد مع زيادة حجم الكتلة. لحسن الحظ ، فإن تكرار هذا الفحص يتضاعف أربع مرات في كل دورة ، بينما تتضاعف الفائدة المحتملة أربع مرات في كل دورة.
في حالة وجود الكتل الأربع بترتيب عكسي ، يتم إجراء مقايضة ثابتة في المكان.
في حالة أن اثنين فقط من الكتل الأربعة مرتبة أو بترتيب عكسي ، فإن المقارنات في الدمج نفسه غير ضرورية ويتم حذفها لاحقًا. لا تزال البيانات بحاجة إلى النسخ في ذاكرة المبادلة ، لكن هذا إجراء أقل حسابية.
يسمح هذا لخوارزمية الترتيب الرباعي بفرز التسلسلات بالترتيب الأمامي والخلفي باستخدام
nالمقارنات بدلاً من n * log nالمقارنات.
الشيكات الحدودية
هناك مشكلة أخرى تتعلق بفرز الدمج التقليدي وهي أنها تهدر الموارد على عمليات فحص الحدود غير الضرورية. تبدو هكذا:
while (a <= a_max && b <= b_max)
if (a <= b)
[insert a++]
else
[insert b++]من أجل التحسين ، تقارن الخوارزمية الخاصة بنا العنصر الأخير في التسلسل A مع العنصر الأخير في التسلسل B. إذا كان العنصر الأخير في التسلسل A أقل من العنصر الأخير في التسلسل B ، فإننا نعلم أن الاختبار
b < b_maxسيكون دائمًا خاطئًا ، لأن التسلسل A هو أول عنصر يتم دمجه تمامًا.
وبالمثل ، إذا كان العنصر الأخير في التسلسل A أكبر من العنصر الأخير في التسلسل B ، فإننا نعلم أن الاختبار
a < a_maxسيكون دائمًا خاطئًا. تبدو هكذا:
if (val[a_max] <= val[b_max])
while (a <= a_max)
{
while (a > b)
[insert b++]
[insert a++]
}
else
while (b <= b_max)
{
while (a <= b)
[insert a++]
[insert b++]
}ذيل الانصهار
عندما تقوم بفرز مصفوفة مكونة من 65 عنصرًا ، ينتهي بك الأمر بمصفوفة مرتبة مكونة من 64 عنصرًا ومصفوفة مرتبة عنصرًا واحدًا في النهاية. لن يؤدي هذا إلى عملية مبادلة (تبادل) إضافية إذا كان التسلسل بأكمله في الترتيب. في أي حال ، لهذا ، يجب أن يختار البرنامج حجم الصفيف الأمثل (64 أو 256 أو 1024).
مشكلة أخرى هي أن حجم المصفوفة دون المستوى الأمثل يؤدي إلى عمليات تبادل غير ضرورية. للتغلب على هاتين المشكلتين ، يتم إحباط إجراء الدمج الرباعي عندما يصل حجم الكتلة إلى 1/8 من حجم الصفيف ويتم فرز باقي الصفيف باستخدام دمج الذيل. الميزة الرئيسية لدمج الذيل هي أنه يمكن أن يقلل من حجم المبادلة الرباعية إلى n / 2 دون التأثير بشكل كبير على الأداء.
O كبير
| اسم | الأفضل | الأوسط | أسوأ | مستقر | ذاكرة |
|---|---|---|---|---|---|
| كوادسورت | ن | ن سجل | ن سجل | نعم | ن |
عندما يتم فرز البيانات بالفعل أو فرزها بترتيب عكسي ، يقوم quadsort بإجراء مقارنات n.
مخبأ
نظرًا لأن quadsort يستخدم مقايضات n / 2 ، فإن استخدام ذاكرة التخزين المؤقت ليس مثاليًا مثل الفرز الموضعي. ومع ذلك ، يؤدي فرز البيانات العشوائية في مكانها إلى تبادلات دون المستوى الأمثل. استنادًا إلى معاييري ، يكون quadsort دائمًا أسرع من التصنيف الموضعي ، طالما أن المصفوفة لا تتجاوز ذاكرة التخزين المؤقت L1 ، والتي يمكن أن تصل إلى 64 كيلوبايت في المعالجات الحديثة.
ولفسورت
Wolfsort هي خوارزمية فرز جذري / رباعية مختلطة تعمل على تحسين الأداء عند العمل مع البيانات العشوائية. هذا في الأساس دليل على المفهوم الذي يعمل فقط مع الأعداد الصحيحة بدون إشارة 32 و 64 بت.
التصور
التصور أدناه يدير أربعة اختبارات. يعتمد الاختبار الأول على التوزيع العشوائي ، والثاني على التوزيع التصاعدي ، والثالث على التوزيع التنازلي ، والرابع على التوزيع التصاعدي ذي الذيل العشوائي.
يظهر النصف العلوي المبادلة ويظهر النصف السفلي الذاكرة الرئيسية. تختلف الألوان لعمليات التخطي والتبديل والدمج والنسخ.
المعيار المرجعي: quadsort و std :: stabil_sort و timsort و pdqsort و wolfsort
تم تشغيل المعيار التالي على إصدار تكوين WSL gcc 7.4.0 (Ubuntu 7.4.0-1ubuntu1 ~ 18.04.1). يتم تجميع شفرة المصدر بواسطة الفريق
g++ -O3 quadsort.cpp. يتم تشغيل كل اختبار مائة مرة ويتم الإبلاغ عن أفضل تشغيل فقط.
الحد الأقصى هو وقت التنفيذ.
ورقة بيانات Quadsort ، الأمراض المنقولة جنسياً :: Stead_sort ، timsort ، pdqsort و wolfsort
| quadsort | 1000000 | i32 | 0.070469 | 0.070635 | ||
| stablesort | 1000000 | i32 | 0.073865 | 0.074078 | ||
| timsort | 1000000 | i32 | 0.089192 | 0.089301 | ||
| pdqsort | 1000000 | i32 | 0.029911 | 0.029948 | ||
| wolfsort | 1000000 | i32 | 0.017359 | 0.017744 | ||
| quadsort | 1000000 | i32 | 0.000485 | 0.000511 | ||
| stablesort | 1000000 | i32 | 0.010188 | 0.010261 | ||
| timsort | 1000000 | i32 | 0.000331 | 0.000342 | ||
| pdqsort | 1000000 | i32 | 0.000863 | 0.000875 | ||
| wolfsort | 1000000 | i32 | 0.000539 | 0.000579 | ||
| quadsort | 1000000 | i32 | 0.008901 | 0.008934 | () | |
| stablesort | 1000000 | i32 | 0.017093 | 0.017275 | () | |
| timsort | 1000000 | i32 | 0.008615 | 0.008674 | () | |
| pdqsort | 1000000 | i32 | 0.047785 | 0.047921 | () | |
| wolfsort | 1000000 | i32 | 0.012490 | 0.012554 | () | |
| quadsort | 1000000 | i32 | 0.038260 | 0.038343 | ||
| stablesort | 1000000 | i32 | 0.042292 | 0.042388 | ||
| timsort | 1000000 | i32 | 0.055855 | 0.055967 | ||
| pdqsort | 1000000 | i32 | 0.008093 | 0.008168 | ||
| wolfsort | 1000000 | i32 | 0.038320 | 0.038417 | ||
| quadsort | 1000000 | i32 | 0.000559 | 0.000576 | ||
| stablesort | 1000000 | i32 | 0.010343 | 0.010438 | ||
| timsort | 1000000 | i32 | 0.000891 | 0.000900 | ||
| pdqsort | 1000000 | i32 | 0.001882 | 0.001897 | ||
| wolfsort | 1000000 | i32 | 0.000604 | 0.000625 | ||
| quadsort | 1000000 | i32 | 0.006174 | 0.006245 | ||
| stablesort | 1000000 | i32 | 0.014679 | 0.014767 | ||
| timsort | 1000000 | i32 | 0.006419 | 0.006468 | ||
| pdqsort | 1000000 | i32 | 0.016603 | 0.016629 | ||
| wolfsort | 1000000 | i32 | 0.006264 | 0.006329 | ||
| quadsort | 1000000 | i32 | 0.018675 | 0.018729 | ||
| stablesort | 1000000 | i32 | 0.026384 | 0.026508 | ||
| timsort | 1000000 | i32 | 0.023226 | 0.023395 | ||
| pdqsort | 1000000 | i32 | 0.028599 | 0.028674 | ||
| wolfsort | 1000000 | i32 | 0.009517 | 0.009631 | ||
| quadsort | 1000000 | i32 | 0.037593 | 0.037679 | ||
| stablesort | 1000000 | i32 | 0.043755 | 0.043899 | ||
| timsort | 1000000 | i32 | 0.047008 | 0.047112 | ||
| pdqsort | 1000000 | i32 | 0.029800 | 0.029847 | ||
| wolfsort | 1000000 | i32 | 0.013238 | 0.013355 | ||
| quadsort | 1000000 | i32 | 0.009605 | 0.009673 | ||
| stablesort | 1000000 | i32 | 0.013667 | 0.013785 | ||
| timsort | 1000000 | i32 | 0.007994 | 0.008138 | ||
| pdqsort | 1000000 | i32 | 0.024683 | 0.024727 | ||
| wolfsort | 1000000 | i32 | 0.009642 | 0.009709 |
وتجدر الإشارة إلى أن pdqsort ليس نوعًا مستقرًا ، لذا فهو يعمل بشكل أسرع مع البيانات بالترتيب الطبيعي (ترتيب عام).
تم تشغيل المعيار التالي على WSL gcc الإصدار 7.4.0 (Ubuntu 7.4.0-1ubuntu1 ~ 18.04.1). يتم تجميع شفرة المصدر بواسطة الفريق
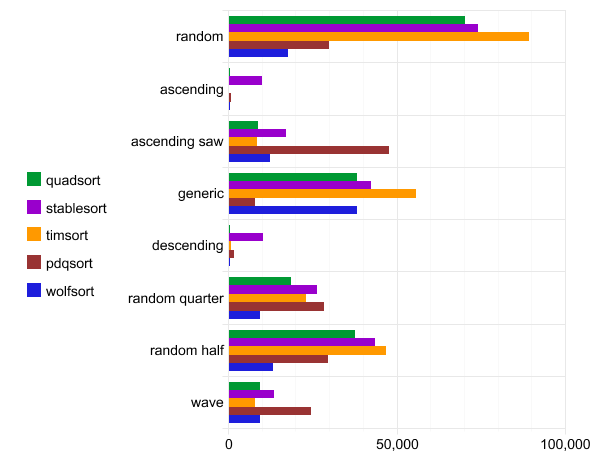
g++ -O3 quadsort.cpp. يتم تشغيل كل اختبار مائة مرة ويتم الإبلاغ عن أفضل تشغيل فقط. يقيس الأداء على المصفوفات التي تتراوح من 675 إلى 100000 عنصر.
المحور X في الرسم البياني أدناه هو العلاقة الأساسية ، والمحور Y هو وقت التنفيذ.

ورقة بيانات Quadsort ، الأمراض المنقولة جنسياً :: Stead_sort ، timsort ، pdqsort و wolfsort
| quadsort | 100000 | i32 | 0.005800 | 0.005835 | ||
| stablesort | 100000 | i32 | 0.006092 | 0.006122 | ||
| timsort | 100000 | i32 | 0.007605 | 0.007656 | ||
| pdqsort | 100000 | i32 | 0.002648 | 0.002670 | ||
| wolfsort | 100000 | i32 | 0.001148 | 0.001168 | ||
| quadsort | 10000 | i32 | 0.004568 | 0.004593 | ||
| stablesort | 10000 | i32 | 0.004813 | 0.004923 | ||
| timsort | 10000 | i32 | 0.006326 | 0.006376 | ||
| pdqsort | 10000 | i32 | 0.002345 | 0.002373 | ||
| wolfsort | 10000 | i32 | 0.001256 | 0.001274 | ||
| quadsort | 5000 | i32 | 0.004076 | 0.004086 | ||
| stablesort | 5000 | i32 | 0.004394 | 0.004420 | ||
| timsort | 5000 | i32 | 0.005901 | 0.005938 | ||
| pdqsort | 5000 | i32 | 0.002093 | 0.002107 | ||
| wolfsort | 5000 | i32 | 0.000968 | 0.001086 | ||
| quadsort | 2500 | i32 | 0.003196 | 0.003303 | ||
| stablesort | 2500 | i32 | 0.003801 | 0.003942 | ||
| timsort | 2500 | i32 | 0.005296 | 0.005322 | ||
| pdqsort | 2500 | i32 | 0.001606 | 0.001661 | ||
| wolfsort | 2500 | i32 | 0.000509 | 0.000520 | ||
| quadsort | 1250 | i32 | 0.001767 | 0.001823 | ||
| stablesort | 1250 | i32 | 0.002812 | 0.002887 | ||
| timsort | 1250 | i32 | 0.003789 | 0.003865 | ||
| pdqsort | 1250 | i32 | 0.001036 | 0.001325 | ||
| wolfsort | 1250 | i32 | 0.000534 | 0.000655 | ||
| quadsort | 675 | i32 | 0.000368 | 0.000592 | ||
| stablesort | 675 | i32 | 0.000974 | 0.001160 | ||
| timsort | 675 | i32 | 0.000896 | 0.000948 | ||
| pdqsort | 675 | i32 | 0.000489 | 0.000531 | ||
| wolfsort | 675 | i32 | 0.000283 | 0.000308 |
المعيار: quadsort و qsort (mergesort)
تم تشغيل المعيار التالي على WSL gcc الإصدار 7.4.0 (Ubuntu 7.4.0-1ubuntu1 ~ 18.04.1). يتم تجميع شفرة المصدر بواسطة الفريق
g++ -O3 quadsort.cpp. يتم تشغيل كل اختبار مائة مرة ويتم الإبلاغ عن أفضل تشغيل فقط.
quadsort: sorted 1000000 i32s in 0.119437 seconds. MO: 19308657 ( )
qsort: sorted 1000000 i32s in 0.133077 seconds. MO: 21083741 ( )
quadsort: sorted 1000000 i32s in 0.002071 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.007265 seconds. MO: 3000004 ()
quadsort: sorted 1000000 i32s in 0.019239 seconds. MO: 4007580 ( )
qsort: sorted 1000000 i32s in 0.071322 seconds. MO: 20665677 ( )
quadsort: sorted 1000000 i32s in 0.076605 seconds. MO: 19242642 ( )
qsort: sorted 1000000 i32s in 0.038389 seconds. MO: 6221917 ( )
quadsort: sorted 1000000 i32s in 0.002305 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.009659 seconds. MO: 4000015 ()
quadsort: sorted 1000000 i32s in 0.022940 seconds. MO: 9519209 ( )
qsort: sorted 1000000 i32s in 0.042135 seconds. MO: 13152042 ( )
quadsort: sorted 1000000 i32s in 0.034456 seconds. MO: 6787656 ( )
qsort: sorted 1000000 i32s in 0.098691 seconds. MO: 20584424 ( )
quadsort: sorted 1000000 i32s in 0.066240 seconds. MO: 11383441 ( )
qsort: sorted 1000000 i32s in 0.118086 seconds. MO: 20572142 ( )
quadsort: sorted 1000000 i32s in 0.038116 seconds. MO: 15328606 ( )
qsort: sorted 1000000 i32s in 4.471858 seconds. MO: 1974047339 ( )
quadsort: sorted 1000000 i32s in 0.060989 seconds. MO: 15328606 ()
qsort: sorted 1000000 i32s in 0.043175 seconds. MO: 10333679 ()
quadsort: sorted 1023 i32s in 0.016126 seconds. (random 1-1023)
qsort: sorted 1023 i32s in 0.033132 seconds. (random 1-1023)يشير MO إلى عدد المقارنات التي تم إجراؤها على مليون عنصر.
يقارن المعيار أعلاه quadsort إلى glibc qsort () عبر نفس واجهة الغرض العام وبدون أي مزايا غير عادلة معروفة مثل التضمين.
random order: 635, 202, 47, 229, etc
ascending order: 1, 2, 3, 4, etc
uniform order: 1, 1, 1, 1, etc
descending order: 999, 998, 997, 996, etc
wave order: 100, 1, 102, 2, 103, 3, etc
stable/unstable: 100, 1, 102, 1, 103, 1, etc
random range: time to sort 1000 arrays ranging from size 0 to 999 containing random dataالمعيار: quadsort و qsort (الترتيب السريع)
يتم إجراء هذا الاختبار الخاص باستخدام تنفيذ () Cygwin's qsort ، والذي يستخدم الفرز السريع تحت الغطاء. يتم تجميع شفرة المصدر بواسطة الفريق
gcc -O3 quadsort.c. يتم تنفيذ كل اختبار مائة مرة ، ويتم الإبلاغ عن أفضل تشغيل فقط.
quadsort: sorted 1000000 i32s in 0.119437 seconds. MO: 19308657 ( )
qsort: sorted 1000000 i32s in 0.133077 seconds. MO: 21083741 ( )
quadsort: sorted 1000000 i32s in 0.002071 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.007265 seconds. MO: 3000004 ()
quadsort: sorted 1000000 i32s in 0.019239 seconds. MO: 4007580 ( )
qsort: sorted 1000000 i32s in 0.071322 seconds. MO: 20665677 ( )
quadsort: sorted 1000000 i32s in 0.076605 seconds. MO: 19242642 ( )
qsort: sorted 1000000 i32s in 0.038389 seconds. MO: 6221917 ( )
quadsort: sorted 1000000 i32s in 0.002305 seconds. MO: 999999 ()
qsort: sorted 1000000 i32s in 0.009659 seconds. MO: 4000015 ()
quadsort: sorted 1000000 i32s in 0.022940 seconds. MO: 9519209 ( )
qsort: sorted 1000000 i32s in 0.042135 seconds. MO: 13152042 ( )
quadsort: sorted 1000000 i32s in 0.034456 seconds. MO: 6787656 ( )
qsort: sorted 1000000 i32s in 0.098691 seconds. MO: 20584424 ( )
quadsort: sorted 1000000 i32s in 0.066240 seconds. MO: 11383441 ( )
qsort: sorted 1000000 i32s in 0.118086 seconds. MO: 20572142 ( )
quadsort: sorted 1000000 i32s in 0.038116 seconds. MO: 15328606 ( )
qsort: sorted 1000000 i32s in 4.471858 seconds. MO: 1974047339 ( )
quadsort: sorted 1000000 i32s in 0.060989 seconds. MO: 15328606 ()
qsort: sorted 1000000 i32s in 0.043175 seconds. MO: 10333679 ()
quadsort: sorted 1023 i32s in 0.016126 seconds. (random 1-1023)
qsort: sorted 1023 i32s in 0.033132 seconds. (random 1-1023)في هذا المعيار ، يتضح سبب تفضيل التصنيف السريع على الدمج التقليدي ، حيث يقوم بإجراء مقارنات أقل للبيانات بترتيب تصاعدي ، وموزعة بشكل موحد ، وللبيانات بترتيب تنازلي. ومع ذلك ، في معظم الاختبارات كان أداؤها أسوأ من كوادسورت. يُظهر Quicksort أيضًا سرعة فرز بطيئة للغاية للبيانات ذات الترتيب الموجي. يُظهر اختبار البيانات العشوائية أن quadsort أسرع بمرتين عند فرز المصفوفات الصغيرة.
Quicksort أسرع في اختبارات الأغراض العامة والمستقرة ، ولكن فقط لأنها خوارزمية غير مستقرة.
أنظر أيضا:
- " عودة لوموتو المظفرة "
- " ارتفاع فرز حفنة من "
- " الفرز بالشجرة الديكارتية "