مرحبا سكان! العملاق بأقدام من الطين هو ما يمكنك تسميته بالمبرمج دون تدريب في علوم الكمبيوتر. يتيح لك إتقان الأساسيات الواثق عدم "إعادة اختراع العجلة" وبناء حلول فعالة في بنية البرنامج. كل هذا يزيل الأخطاء والتكاليف الباهظة للاختبار وإعادة البناء.
لا يهم إذا كنت تشعر بأنك في غير محله عندما يناقش المبرمجون الآخرون الحد التقريبي. حتى الخبراء المتمرسون يرتكبون أخطاء لأنهم نسوا علوم الكمبيوتر.
لماذا هذا الكتاب مطلوب
دخل العديد من زملائي المطورين (المؤلفين) في المهنة من مجموعة متنوعة من المجالات. البعض حاصل على تعليم عالي في علوم الكمبيوتر ؛ درس آخرون التصوير الفوتوغرافي والرياضيات أو حتى تخرجوا من الجامعة.
لاحظت في السنوات الأخيرة أن المبرمجين يتوقون بشكل متزايد إلى تعلم علوم الكمبيوتر لعدد من الأسباب:
- ليصبحوا مبرمجين جيدين ؛
- للإجابة على أسئلة حول الخوارزميات أثناء المقابلات ؛
- لإرضاء فضولهم حول علوم الكمبيوتر ، أو للتوقف أخيرًا عن الأسف لأنه في وقت من الأوقات لم تتح لهم الفرصة لإتقان هذا الموضوع.
هذا الكتاب لكم جميعا.
سيجد الكثير هنا موضوعات مثيرة للاهتمام في حد ذاتها. حاولت أن أظهر في المواقف الحقيقية (غير الأكاديمية) هذه المعرفة ستكون مفيدة. بعد قراءة هذا الكتاب ، أريدك أن تكتسب نفس المعرفة التي اكتسبتها بعد دراسة الدورة الأساسية في علوم الكمبيوتر ، وكذلك تعلم كيفية تطبيقها.
ببساطة ، الغرض من هذا الكتاب هو مساعدتك في أن تصبح مبرمجًا أكثر مهارة وخبرة من خلال فهم أفضل لعلوم الكمبيوتر. لا يمكنني حصر 20 عامًا من التدريس الجامعي والخبرة المهنية في كتاب واحد ... لكنني سأحاول بذل قصارى جهدي. آمل أن تجد هنا موضوعًا واحدًا على الأقل ، يمكنك أن تقول عنه: "نعم ، الآن أفهمه" ، وتطبيق المعرفة في عملك.
ما لن تجده في الإصدار
معنى الكتاب هو مساعدة القارئ على فهم علوم الكمبيوتر بشكل أفضل وتطبيق المعرفة في الممارسة العملية ، وليس على الإطلاق استبدال أربع سنوات من الدراسة تمامًا.
على وجه الخصوص ، هذا ليس كتاب إثبات. في الواقع ، في المجلد الثاني من الكتاب ، يتم النظر في طرق الإثبات ، ولكن عادةً ما يتم تقديم الخوارزميات القياسية هنا بدون أدلة. الفكرة هي أن يعرف القارئ عن وجود هذه الخوارزميات وأن يتعلم كيفية استخدامها دون الخوض في التفاصيل. ككتاب إثبات مكتوب للطلاب الجامعيين والخريجين ، أوصي بشدة بمقدمة إلى الخوارزميات بواسطة Cormen و Leiserson و Rivest و Stein (عادةً ما يتم تجميع المؤلفين تحت اختصار CLRS).
هذا ليس كتاب برمجة أيضًا: لن تجد إرشادات حول وقت استخدام أرقام من النوع int ومتى تستخدم double ، أو شرحًا لماهية الحلقة. من المفترض أن القارئ يمكنه فهم قوائم الأكواد الكاذبة المستخدمة لوصف الخوارزميات (جميع البرامج في هذا الكتاب مكتوبة بالرمز الزائف بناءً على لغة سي). الغرض من الكتاب هو ربط مفاهيم علوم الكمبيوتر بتقنيات البرمجة المألوفة بالفعل للقارئ.
10. البرمجة الديناميكية
10.1. مشكلة الحقول المفقودة
افترض أن لدينا رقعة شطرنج n × n مفقودة عدة مربعات. كيف تجد أكبر قطعة من لوح ك × ك بدون الحقول المفقودة؟
إذا لم تكن قد واجهت مثل هذه المشكلة من قبل ، فاخذ بضع دقائق لكتابة حل وتحديد وقت تنفيذ الخوارزمية.
في مواجهة هذه المشكلة ، فكرت على النحو التالي. يمكن أن ينتمي كل حقل رقعة شطرنج إلى العديد من أكبر المناطق ، ولكن يمكن أن يكون في الزاوية اليسرى العليا في واحدة منها فقط. إذا قمت بتمييز كل مربع بحجم أكبر منطقة سليمة تكون فيها الزاوية اليسرى العليا ، فإن المربع الذي يحتوي على أكبر علامة من هذا القبيل سيتوافق مع المنطقة المطلوبة.
افترض أن اللوحة ممثلة كمصفوفة n × n حيث تحتوي كل خلية على 1 إذا كان الحقل المقابل موجودًا و 0 إذا كان مفقودًا. إذا كانت قيمة الخلية الحالية تساوي 0 ، فحينئذٍ يكون الحقل المقابل غائبًا ولا يمكن أن يكون جزءًا من مقطع مجاور ، لذلك لا يلزم تغييره. إذا كانت القيمة 1 ، فيمكننا استبدالها برقم يزيد بمقدار واحد عن الحد الأدنى لقيمة الخلايا الثلاث الموجودة أدناه وإلى اليمين.
نقوم بتغيير كل خلية في المصفوفة مرة واحدة ، بما في ذلك التحقق مما إذا كانت قيمة الخلية صفر ، والتحقق من قيم ما يصل إلى ثلاث خلايا أخرى ، وكتابة قيمة الخلية الجديدة. تستغرق كل عملية من هذه العمليات وقت O (1) ، وبالتالي فإن الوقت الذي تستغرقه معالجة لوحة الداما بالكامل هو
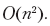
لاحظ أن هذا هو وقت تنفيذ الخوارزمية الخطي ، وليس التربيعي - على رقعة الشطرنج n (نفترض أن n هو العدد الإجمالي للحقول ، ونحن نلتزم بالاتفاقية المعتادة بأن n هي كمية بيانات الإدخال) الحقول (بعضها عبارة عن غائب) ، وبالتالي فإن إجمالي الوقت الذي تقضيه الخوارزمية يتناسب مع عدد الحقول. إذا أشرنا بدقة أكبر إلى حجم رقعة الشطرنج كـ √ n × √ n ، فسنحصل على n من الحقول ووقت التنفيذ الإجمالي هو O (n).
10.2. العمل مع المهام الفرعية المتداخلة
الطريقة المستخدمة في هذا القسم تسمى البرمجة الديناميكية. يتم استخدامه عندما يمكن تقسيم المشكلة إلى عدة مهام فرعية ، سيتم استخدام حل كل منها عدة مرات. يختلف هذا النهج عن مبدأ "فرق تسد" ، عندما تنقسم المشكلة إلى مهام فرعية ، يتم حلها بشكل مستقل عن بعضها البعض. في مشكلة رقعة الشطرنج ، اعتمدت كل مشكلة فرعية على حلول لثلاث مشاكل أخرى ، وتم حفظ الحلول لجميع المشكلات الفرعية لاستخدامها مرة أخرى.
عادة ما تتم البرمجة الديناميكية عن طريق بناء الجداول كما هو موضح أعلاه. هذا يعني حل مشكلة باستخدام نهج من أسفل إلى أعلى ، حيث نبدأ بحل أصغر المشكلات الفرعية ونعمل في طريقنا حتى نتوصل إلى إجابة. طريقة أخرى هي الحفظ ، حيث ننتقل من أعلى إلى أسفل ، وحل المشكلات الفرعية حسب الحاجة وتخزين النتائج مؤقتًا لإعادة استخدامها. تعد طاولات البناء هي الخيار المفضل عندما تحتاج إلى حل كل مشكلة فرعية (في المثال الخاص بي باستخدام رقعة الشطرنج ، كان من الضروري العثور على أكبر مساحة سليمة لكل مجال من مجالات اللوحة) ، نظرًا لأن تكاليف هذه الطريقة أقل من تكلفة الذاكرة. إذا لم يكن من الضروري حل بعض المهام الفرعية من منطقة الحل ، فإن الحفظ يسمح لك فقط بحل تلك المهام الفرعية الضرورية حقًا.
تتضمن النقطة الأساسية
حيث تقسم تسد تقسيم مهمة إلى عدة مهام فرعية مستقلة ، وتعني البرمجة الديناميكية تقسيم المهمة إلى عدة مهام فرعية متداخلة. يتم تخزين حل كل مشكلة فرعية مؤقتًا لإعادة استخدامه لاحقًا.
10.3. البرمجة الديناميكية وأقصر المسارات
ضع في اعتبارك مشكلة العثور على أقصر مسار: بالنسبة إلى رسم بياني محدد ذي حواف مرجحة ، تحتاج إلى العثور على مسار من عقدة إلى أخرى بأقل تكلفة.
التعريف
الرسم البياني المرجح بالحافة هو رسم بياني يكون لكل حافة وزنه الخاص (التكلفة). يتم تحديد تكلفة المسار من عقدة إلى أخرى من خلال مجموع تكلفة جميع الحواف المقطوعة.
لنفترض أننا وجدنا مسارًا بين العقدتين s و t يحتوي على العقدة الثالثة v. ثم يجب أن يحتوي المسار من s إلى t على أقصر مسار من s إلى v ، لأنه بخلاف ذلك يمكننا استبدال هذا المقطع بمسار أقصر وتقليل طول أقصر مسار من s إلى t ، وهو ما يتعارض مع الشرط الأولي (هذا هو مبدأ Bellman الأمثل).
( ) , . , . , .
, , .
تعتبر مشكلات العثور على أقصر مسار أمثلة مذهلة على البرمجة الديناميكية ، نظرًا لأن الخاصية المثلى للبنية التحتية واضحة بشكل بديهي - فمن الواضح أن أسرع طريقة للانتقال من النقطة A إلى النقطة C عبر النقطة B هي أيضًا أسرع طريقة للانتقال من النقطة A إلى النقطة B ومن النقطة B إلى النقطة C. يشتمل عدد الخوارزميات القائمة على هذا المبدأ على طريقة Bellman - Ford ، التي تعثر على أقصر مسار من نقطة البداية إلى أي قمة للرسم البياني (أو من أي قمة للرسم البياني إلى نقطة النهاية) وطريقة Floyd - Warshall - بمساعدتها يتم حساب أقصر مسار بين كل زوج من رؤوس الرسم البياني. في كلتا الحالتين ، تكمن الفكرة في البدء بمجموعة فرعية صغيرة من العقد القريبة من العقد ذات الأهمية ، ثم توسيع هذه المجموعة تدريجيًا باستخدام العقد الموجودة بالفعل لحساب مسافات جديدة.
10.4.
10.4.1. Git merge
هناك مهمة أخرى تُستخدم بشكل شائع لإثبات البرمجة الديناميكية وهي إيجاد أطول تتابع مشترك. تتمثل المهمة في العثور على أطول سلسلة تحدث في كلتا السلسلتين مع الحفاظ على تسلسل الأحرف. لا يجب أن تكون الأوتار متتالية ؛ على سبيل المثال ، إذا كان A = {acdbef} و B = {babdef} ، فإن {adef} سيكون نتيجة لاحقة شائعة.
عند دمج التغييرات في Git (الدمج) ، فإنه يبحث عن أكبر نتيجة مشتركة للفروع الرئيسية والفروع العاملة. تتم إزالة الأحرف الموجودة في اللغة الرئيسية ولكنها غير موجودة في أكبر تتابعات مشتركة ؛ تتم إضافة الأحرف الموجودة في فرع العمل ولكنها ليست في هذه اللاحقة إلى الماجستير.
10.4.2. LATEX
غالبًا ما يستخدم نظام إعداد المستندات LATEX لإنشاء المستندات الفنية. تتمثل إحدى مهام نظام الكتابة في محاذاة النص إلى اليمين واليسار في نفس الوقت ؛ للقيام بذلك ، يتم تمديد أو تقليص التباعد بين الكلمات والحروف بحيث يكون لكل الأسطر نفس الطول. هناك طريقة أخرى لمحاذاة النص وهي التفاف الكلمة الأخيرة بحيث يظهر هذا الجزء من الكلمة في السطر التالي. LATEX (من وجهة نظر فنية ، يقوم نظام إدخال نص TEX بكل العمل تقريبًا ؛ LATEX مبني على قمة TEX. هنا أستخدم LATEX لأسباب تتعلق بالبساطة) يحاول العثور على أفضل نقاط فواصل الأسطر لجعل النص يبدو جميلًا. إذا فشل ذلك ، فستنتهي عدة أسطر متتالية بواصلة كلمة ، أو ستختلف المسافة بين الكلمات في سطور مختلفة.لدى لاتكس مجموعة من القواعد لتقييم "فشل" المحاذاة. يسعى البرنامج إلى إيجاد الخيار "الأقل سوءًا".
إذا كان هناك عدد من نقاط فواصل الأسطر في فقرة ، فهناك
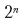خيارات محتملة لكسر النص. يعتمد "فشل" التحديد لكل نقطة فاصل على نقاط الفاصل التي تم تحديدها قبلها. وبالتالي ، لدينا مهام فرعية متداخلة مرة أخرى. يقلل استخدام تقنيات البرمجة الديناميكية من وقت التنفيذ 
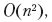الذي يمكن تحسينه بطرق إضافية.
»يمكن العثور على مزيد من التفاصيل حول الكتاب على الموقع الإلكتروني لدار النشر
» جدول المحتويات
» مقتطفات
للساكنين خصم 25٪ على القسيمة - علوم الكمبيوتر
عند الدفع مقابل النسخة الورقية من الكتاب ، يتم إرسال كتاب إلكتروني إلى البريد الإلكتروني.