النموذج الرياضي للظاهرة أن جميع العمليات تتم في الزمكان 4-الأبعاد ، حيث تتبع ظواهر SRT من الحفاظ على الفاصل الزمني للأحداث أثناء تحويل دوران نظام الإحداثيات. لا يمكن إنكار أن الواقع ، كما هو ، ممتد على الإنشاءات الرياضية. علاوة على ذلك ، فإن حقيقة أن الأرقام الخيالية ، في الواقع التي لا يمكن تصورها ، تلعب دورًا مهمًا تقريبًا فيها ، لا تقلل من نجاح العلم. حتى إي.ماك قال إن التفسيرات غير ضرورية إذا تم وصف الظواهر المرصودة جيدًا بالصيغ. ودعونا لا نتجادل مع هذا النقد التجريبي.
يخترع علماء الرياضيات التجريد ويجربوها على أرض الواقع. ومن ثم التفرد والثقب وغيرها من الأشياء الغريبة. أو ربما يستحق التخيل ، على سبيل المثال ، حول ما يمكن أن يتغير في أفكارنا حول العالم إذا كان سبب تقلص لورنتز هو بعض الآليات الفيزيائية المفترضة. لما لا؟
1 السبب الجسدي لانقباض لورنتز
أولاً ، سأعبر عن المبدأ الواضح الذي يبدو أن الجسيمات والذرات والجزيئات تتفاعل مع بعضها البعض من خلال المجالات الفيزيائية . يمكننا بالطبع أن نقول أنهم يتبادلون جسيمات الكم ، لكننا نلعب الآن في مجال النظرية النسبية ، لذلك سننسى الآن الكمي. لذا ، فإن الافتراض الأول الرائع هو أنه على وجه التحديد بسبب التوازن المتبادل للتأثيرات الميدانية التي تتم إضافة الجسيمات إلى تكوين وشكل معين . إذا انحرف أي جسيم عن وضع التوازن ، فسوف ينطلق اضطراب المجال منه ، مما سيؤدي إلى تحريك بقية الجسيمات ، مما سيؤدي بدوره إلى تأثير مجال عكسي منها على هذا الجسيم.
و الثاني الافتراض هو أنينتشر اضطراب المجال في مساحة مشتركة معينة بسرعة معينة . والطبيعة الرائعة لهذا الافتراض هي أنه وفقًا للعلم ، فإن المجال موجود بمفرده في الزمكان رباعي الأبعاد (P-W) ولا ينتشر فوق أي شيء. بشكل عام ، إنه أمر صعب في العلوم ... سنفترض أن الحقول تنتشر وتوجد في مساحة واحدة ثلاثية الأبعاد - حيث نحن والأرض والنجوم. يبدو أن هذا غني عن القول ومن لا يعرف ، ولكن دعونا نرى ما سيحدث. أولئك الذين لا يرغبون في الإزعاج بالصيغ يمكن أن يقتصروا على قراءة النص المحدد فقط.
لذا ، نتفق على أن هناك وقت تفاعل بين الجسيماتوالتي تتكون من وقت وصول السخط عليهم ووقت عودة الجواب منهم. ونتيجة لذلك ، سيتم إنشاء التكوين السابق للجسم تدريجيًا مرة أخرى. الشكل 1 التأثيرات الميدانية التي تحدد موضع الجسيم
لأي نقطة من الجسم ، من الممكن التمييز بين مجموعات النقاط التي سيكون لها فيها أوقات تفاعل متساوية والتي سوف نسميها متساوية مع هذه النقطة. ينعكس الوضع في الشكل 1. بطبيعة الحال ، في حالة الراحة ، فإن مجال أي نصف قطر راحة R حول نقطة ما هو موضع النقاط (GMT) متزامن معها.
لاحظ أن حركة الجسيم في كل لحظة يتم تحديدها من خلال مجموع القوى الناتجة التي يتم تطبيقها في وقت واحد من مجمل جميع مجموعات الجسيمات المتزامنة معها... دعنا نحاول معرفة كيف سيتغير سطح GMT ، المكون من مجموعة من النقاط 2 ، 3 ، وما إلى ذلك ، عندما يتحرك الجسم. مع نفس أوقات التفاعل مع النقطة 1 ، والتي قد لا تكون مجالًا بعد الآن.
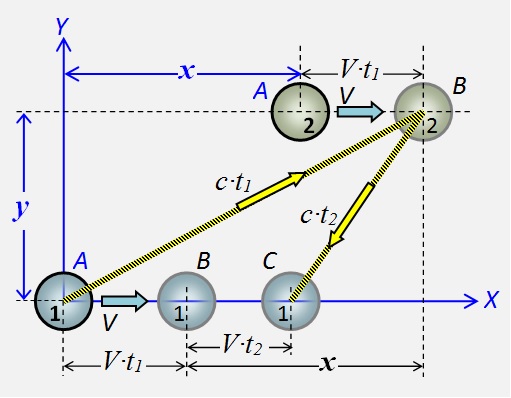دعونا نقاط الجسم 1 و 2 يتم إصلاحها بشكل متبادل ومتزامن تحريك الحق مع سرعة V . عندما تكون نقطة واحدة في الأصل ، يتم إرسال حقل الاضطراب إلى النقطة 2. الترتيب المتبادل للنقاط المميزة بالحرف أ . الشكل 2 مخطط التفاعلات الميدانية لنقاط الجسم - ذهابًا وإيابًا
عندما يصل الاضطراب إلى النقطة 2 ، سيقطع المسافة V ∙ t 1 . تميزت مواقف نقاط بحرف B . خلال الوقت الذي يعود فيه الاضطراب من النقطة 2 إلى النقطة 1 ، ستغطي النقطة 2 المسافةV ∙ t 2 . ويتميز المركز الجديد مع وC .
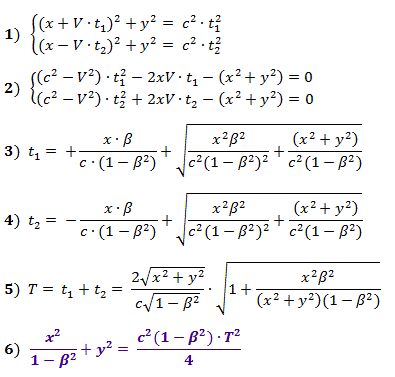الصيغ (1) ، وفقًا لنظرية فيثاغورس ، تصف المسافات في الشكل 2 ، والتي تم الحصول عليها منها (2) هي معادلات لحساب الأوقات t 1 و t 2 ، يتم إعطاء قيمها بالصيغ (3) و (4) للقيم الإيجابية للجذور ، حيث β = V / ج .
تعطي الصيغة (5) قيمة وقت التفاعل من إرسال اضطراب إلى تلقي استجابة.
من (5) نحصل على المعادلة (6) للإحداثيات x و y للمكان الهندسي للنقاط المتزامنة التي يكون فيها وقت التفاعل للنقطة 1 هو نفسه.
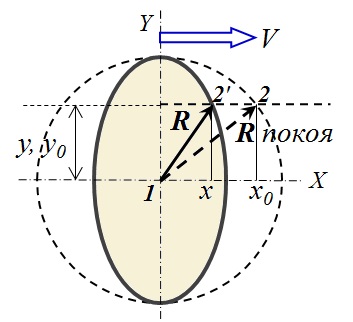تصف الصيغة (6) الجزء البيضوي الموضح في الشكل 3 ، والمضغوط على طول اتجاه الحركة (على طول المحور X) بمقدار √ (1 - β 2 ) مرات ، أي ، وفقًا لصيغة Lorentz. النقطة 2 على سطح الكرة عند الراحة ، أثناء الحركة ، ستنتقل إلى الموضع 2 ' . في هذه الحالة ، ستظل النقاط المادية التي كانت متزامنة مع النقطة 1 عند الراحة متساوية معها أثناء الحركة . الشكل 3
لذلك ، عند التحرك ، يتم ضغط جسم مادي وفقًا لـ Lorentz على وجه التحديد لأنه يتم ضغط "صورة" الحقول المادية تمامًا ، مما يضمن سلامتها في الفضاء .
بما أن تقلص لورنتز هو نفسه بالنسبة لجميع النقاط المتساوية المحيطة بكل نقطة من الجسم ، فإن الجسم المتحرك بالكامل سينكمش بشكل متساوٍ على طول محور الحركة.
2. اشتقاق صيغة تمدد الوقت
دعونا نحدد وقت التفاعل عندما يتحرك الكائن مقارنة بوقت التفاعل في حالة الراحة.
تربط الصيغ (7) إحداثيات النقاط أثناء الحركة بإحداثياتها في حالة الراحة وفقًا
للمعادلة (6). تحسب الصيغة (8) وقت التفاعل أثناء الراحة. وقد تم الحصول على الصيغ (9) و (10) من صيغة (6) عن طريق استبدال فيه قيم إحداثيات س و ص و R من بقية من الصيغ (7). تعادل الصيغة (11) (10). الصيغة (12) ، التي تم الحصول عليها من (11) عن طريق استبدال الجانب الأيسر من الصيغة (8) بها ، تربط أوقات التفاعل في الراحة وأثناء الحركة. في الشكل التقليدي ، ينعكس هذا في الصيغة (13) ، حيث T 0 هي الفاصل الزمني بين الأحداث في كائن يستريح ، وT هو الفاصل الزمني بين الأحداث نفسها في الجسم المتحرك.
لذا ، فإن أوقات التفاعل لجميع النقاط في جسم متحرك تزداد بنفس النسبة وفقًا لـ Lorentz مقارنة بوقت التفاعل في الراحة. وفقًا لذلك ، بشكل عام ، فإن جميع العمليات في جسم متحرك تتباطأ في الواقع في نفس المجال .
من السهل فهم سبب تباطؤ الوقت إذا أخذنا في الاعتبار أن اضطراب المجال من الجزء الخلفي من الجسيمات المتفاعلة سيتعين عليه اللحاق بالجزء الأمامي في اتجاه الحركة . عندما تكون سرعة الجسم مساوية تقريبًا لسرعة الضوء ، سيستغرق الأمر وقتًا طويلاً للحاق ، وإذا كانت سرعة الجسم تساوي سرعة الضوء ، فلن تلحق أبدًا. ستتوقف جميع التغييرات في الجسم ويبدو أن الوقت سيتوقف.
3. شرح ظاهرة ثبات سرعة الضوء ، الخ.
لنقم بتجربة فكرية. دع نبض الضوء ينبعث من آخر سيارة في القطار ، والتي يتم استقبالها في سيارته الرئيسية. علينا قياس الوقت T 0 الذي سيستغرقه الضوء لتمرير قطار بطول معروف L 0 في نظامه الخاص. في الدليل ، سنستخدم الافتراضات حول تجانس الفضاء وتماثله ، على وجه الخصوص ، سنفترض نفس نتائج القياس للنصف الأول والثاني من القطار ، وكذلك للاتجاهين الأمامي والخلفي. ولكن ، بشكل دقيق ، هذه الافتراضات صالحة فقط في مكان وزمان التجربة.
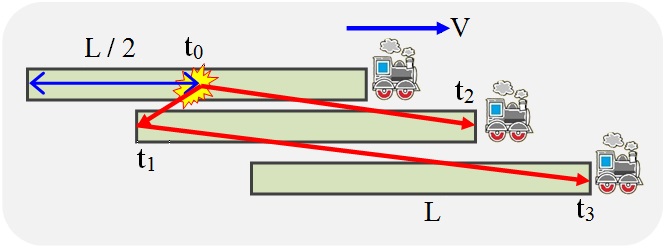
الشكل 4. تجربة فكرية لتحديد سرعة الضوء في قطار متحرك
لمزامنة لحظة إرسال إشارة من السيارة الأخيرة في القطار وبداية عداد الوقت في سيارته الأمامية ، نستخدم نبض ضوئي من منتصف القطار إلى كلا الطرفين.
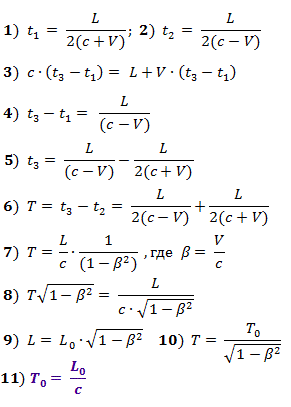
عندما تصل إشارة الانطلاق من منتصف القطار إلى ذيله (الوقت t 1 ) ، سيتم إرسال نبضة ضوئية. عندما تصل إشارة البدء إلى رأس القطار (الوقت t 2 ) ، سيبدأ العد التنازلي حتى وصول النبضة المرسلة.
عندما ينتقل الضوء إلى الذيل ، تضاف سرعته إلى سرعة القطار ، وعندما إلى الرأس ، يتم طرح سرعة القطار. نحصل على العلاقات الواردة أدناه في الصيغ (1) - (6).
الوقت T = t 3 - t 2 هو الفاصل الزمني ،وبحسب المراقب على القطار ، فإنه يفصل أحداث لحظة إرسال الإشارة من نهاية القطار (من لحظة استقبال إشارة الانطلاق هناك) ولحظة استلامه في رأس القطار.
من (6) نحصل على الصيغة (7) ، التي نحولها إلى الشكل (8). علاوة على ذلك ، سنأخذ في الاعتبار أن جميع الكميات L و T و t هنا تقاس في الإطار المرجعي لمراقب خارجي في المكان الذي تجري فيه تجربة التفكير. ولكن عندما يتحرك جسم في الفضاء ، فإن طوله ، كما هو موضح في الفصل 1 ، يخضع في الواقع لانكماش لورنتز ، وأوقات الأحداث ، كما ثبت في الفصل 2، يتباطأ في الواقع بنفس العدد من المرات ، أي استمر لفترة أطول من الراحة ، والتي تنعكس في الصيغ (9) و (10). باستبدال هذه النسب في الصيغة (8) للفاصل T - وقت انتقال الضوء من الذيل إلى رأس القطار ، نحصل على العلاقة (11).
ولكن ما العلاقة التي تربط هذين T 0 و L 0 بالوقت والطول الخاصين بهما للأحداث نفسها ، والتي يتم قياسها في الإطار المرجعي بالقصور الذاتي (IFR) المرتبط بقطار متحرك؟ من الواضح أنهم متساوون . والحقيقة هي أنه يتم التعبير عن الوقت والطول رقميًا من خلال علاقتهما بالمعايير. وفقا لذلك، والقياسات من الزمانية و المكانية وإحداثيات شيء مصنوع في بقية يكون عددياتتساوى مع القياسات نفسها ، والتي تتم في ISO متحرك ، لأنه عند نقل قيم كل من القياسات والمعايير سوف يتغير بشكل متناسب.
السؤال هو كيف تتغير بالضبط عندما تتحرك في الفضاء. تثبت تجربة فكرية مع قطار أنها تتغير بطريقة تجعل القيمة العددية لسرعة الضوء المقاسة في IFR مساوية لقيمة سرعتها في الفضاء . وهذا بالتحديد ما لم يكن دليلاً بديهيًا ومطلوبًا.
نرى أن "افتراض ثبات سرعة الضوء" مشتق من حقيقة انكماش لورنتز وحده ، والذي يُستمد رياضياً من اعتماد موقع المادة المادية على سرعة الانتشار وتكوين المجالات المادية في الفضاء .
من أجل الاكتمال ، دعونا أيضًا نحدد سرعة الضوء عبر حركة القطار ، على سبيل المثال ، بين جدران السيارة على مسافة S 0 عن بعضها البعض. للقيام بذلك ، نقيس وقت حركة نبض الضوء ( 2 · t 0 ) ذهابًا وإيابًا. بالنظر إلى التناظر الواضح بين "هناك" و "رجوع" ، سننظر فقط في "هناك". في نظام المراقب الخارجي ، تحدث الحركة في الفضاء كما هو موضح في الشكل 5.
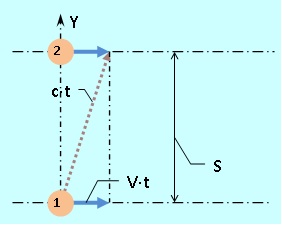ومن ثم لدينا (c · t) 2 = S 2 + (V · t) 2 ، حيث نحصل على t = S / (c · √ (1 - ²²)) ، حيث β = V / c .
في نظام القطار ، انقضى الوقت المناسب t 0متصل بالزمن الذي يمر في الفضاء بالعلاقة t = t 0 / (√ (1 - ²²)) . باستبدال هذا التعبير في صيغة t في الفضاء ، نحصل على t 0 = S / c .
الشكل 5. تجربة فكرية لتحديد سرعة الضوء في قطار متحرك /
في نظام القطار نفسه لنفس t 0 ، لدينا العلاقة t 0 = S 0 / c 0 . ولكن نظرًا لأن الأبعاد المستعرضة لا تتغير أثناء الحركة ، أي S = S 0 ، نحصل على c 0 = c .
أفترض أنه ليست هناك حاجة لإثبات ثبات سرعة الضوء المقاسة للتوجيه التعسفي للحزمة ، مما سيضيف فقط تعقيدًا غير ضروري. بالنظر إلى الثبات الثابت لسرعة الضوء ، من السهل اشتقاق تحويلات لورنتز (L) ، وبدون أي جاذبية لمعادلات ماكسويل أو إلى مساحة مينكوفسكي المجردة رياضياً.
4. اشتقاق تحولات لورنتز
يتكون الحدث من وصول نبضة ضوئية عند النقطة " E " ،
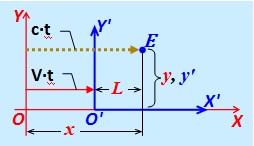تقع في إحداثيات غير متغيرة x ' و y' في النظام المرجعي {X '، Y'} ، تتحرك بسرعة V بالنسبة إلى IFR الثابت {X، Y} ، المرسلة في اللحظة التي تزامنت النقاط O و O 'لكلا المكاتب القطرية. الشكل 6.
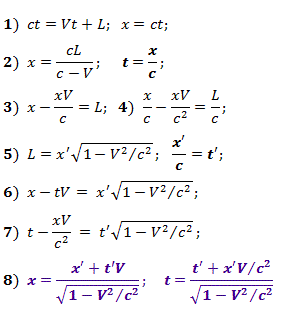في طول CO {X '، Y'} L الخاص به ، مقاسا بـ CO {X، Y} ، ستتم مطابقة إحداثيات x . بالنسبة للحدث ، نظام المعادلات (1) صالح ، والحل الذي نحصل عليه (2) ، ثم (3) و (4).
نظرًا لأن أطوال الأجسام المتحركة يتم ضغطها وفقًا لـ Lorentz ، وأن سرعة الضوء ، كما هو موضح في الفصل 3 ، هي نفسها في أي FR ، ثم بالنسبة إلى x الصحيحوالعلاقات t ' في {X'، Y '} (5) صالحة. استبدال العلاقات من (5) إلى (3) نحصل على (6) ، واستبدالها في (4) ، نحصل على (7). بحكم النسبية للحركة ، يمكننا التفكير في النظام المتحرك {X، Y} ، ولكن بعد ذلك في (6) و (7) من الضروري استبدال المتغيرات غير المظللة بالمتغيرات المظللة ، ويجب أخذ السرعة V بالعلامة المعاكسة ، أو ببساطة حل النظام فيما يتعلق بـ x و t .
نتيجة لذلك ، نحصل على تعبيرات (8) للشكل الأساسي لتحولات لورنتز للإحداثيات ووقت الأحداث في IFRs مختلفة.
عند استخدام PL كطريقة رياضية رسمية بحتة ، تظل الآلية الفيزيائية لظواهر SRT غير واضحة. لذلك ، في مقالاتي السابقة حول تأثير دوبلر النسبيةوالانحرافات الخفيفة ، وكذلك قوانين الانعكاس من مرآة مائلة متحركة ، لم يتم استخدام SLs من حيث المبدأ لتوضيح الأسباب المادية لهذه الظواهر.
5. تبرير مبدأ النسبية وحدود تطبيقه
لاحظ أنه في حالة الراحة في الرسم البياني في الشكل 1 ، فإن الاضطراب من النقطة 1 إلى توقيت غرينتش من النقاط يأتي متزامنًا في وقت واحد ، ثم أثناء الحركة ، في الرسم التخطيطي في الشكل 2 ، لم يعد يتم تحقيق ذلك. في كل نقطة من توقيت جرينتش هذا ، سيتم إنشاء الاستجابة للاضطراب في أوقات مختلفة ، لكنها ستلتقي عند النقطة 1 في وقت واحد . السؤال هو ، هل ستكون النتيجة هي نفسها عند الراحة؟ ثبت
أعلاه أنه في أي IFR فإن الأوقات والمسافات المناسبة المقاسة بين جميع النقاط ستكون هي نفسها كما هي في حالة الراحة . وبالتالي، فإن عدد الفترات، على سبيل المثال، بدأتالموجة الكهرومغناطيسية بين أي نقطة ستكون كما هي في حالة الراحة. نظرًا لأنه يمكن تمثيل اضطراب مجال التكوين التعسفي من خلال التوسع في سلسلة من التوافقيات أحادية اللون ، فإن تكوينات وكثافة جميع المجالات في النظام الجوهري ستكون هي نفسها في حالة الراحة ، على التوالي. ونتيجة لذلك ، لا تنتهك علاقات المرحلة ومزامنة الحقول التي تشكل الجسم ، وستستمر جميع العمليات فيه كما هو الحال أثناء الراحة.
هذا هو بالضبط ما يعلنه "مبدأ النسبية" لأينشتاين ، وكما نرى ، لا بد من استنتاجه رياضيا من افتراضين (انظر الفصل 1) ، اسمحوا لي أن أذكركم: أولا : أن موضع الجسيمات الحقيقية يتم تحديده من خلال بنية الحقول ، وثانيًا ،يحدث انتشار المجال بسرعة محدودة .
أي أن مبدأ النسبية هو بالفعل ، كما كان ، لم يكن بداهة مبدأ عالميًا ، بل نتيجة ، ولديه حدود واضحة للتطبيق . على وجه الخصوص ، سرعة الضوء ليس لها معنى ثابت العالم ، ولكنها سرعة محددة للضوء في منطقة معينة من الفضاء . وقد تختلف في بعض الأماكن بسبب التفاعل مع المجالات الفيزيائية المحلية ، مثل الجاذبية. لذا ، لدينا بديلان ينتجان نفس الصيغ النسبية تمامًا:
- الأول ، الأرثوذكسي والعلمي: يتطلب افتراض مبدأ النسبية المسبق الحقيقي ؛
- : ,
في الحالة الأولى ، لا تتطلب ظواهر SRT شرحًا ، ولا تزال أسبابها وآلياتها غير معروفة. السؤال "لماذا؟" اتضح أنه خارج العلم.
في الحالة الثانية ، تكون الافتراضات منطقية تمامًا ولا شيء مطلوبًا لافتراضها ، وهي "رائعة" فقط بقدر قبول الأسباب الأخرى للنسبية في العلوم. على السؤال "لماذا هي ظاهرة SRT مثل هذا؟" هنا يتم تقديم تفسير واضح وحتى تافه تقريبًا. ولكن هناك حاجة ملحة لمعرفة طبيعة المادة وعلاقتها بالمجالات المادية.
لذلك ، سنستمر في التخيل أكثر.
6. اشتقاق الصيغة E = Mc² ومعادلات الديناميكيات
أولاً ، دعونا نكتشف كيف تتحول القوى بسرعات نسبية. لنحدد عنصر الحجم في الجسم الذي تعمل فيه اللحظات المتوازنة للقوى. عندما يتحرك الجسم ،
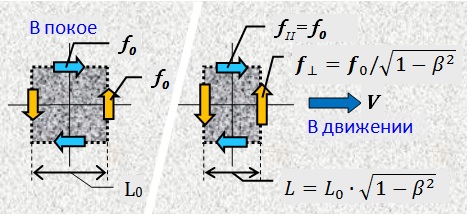سينخفض الحجم الطولي للعنصر المحدد (على طول مسار الحركة) وفقًا لمعامل لورنتز. لكي يظل العنصر متوازنًا ، يجب أن تزيد القوى المتعامدة مع الحركة بنفس النسبة بالضبط. الشكل 7.
إن حجم القوى الموازية للحركة لن يتغير. يجب أن يؤخذ عامل اعتماد القوى على التوجه نسبة إلى اتجاه الحركة في الاعتبار في توسع ناقلات القوى في الصيغ التالية.
لاحظ أن تسريع الجسم إلى سرعة معينة يتم من خلال القوة المطبقة ، والتي ، وفقًا لذلك ، تقوم ببعض الأعمال ، وبالتالي زيادة طاقة الجسم. وما الفرق بين الجسم المتناثر في الفضاء والجسد في حالة الراحة؟ حقيقة أن زيادة سرعة التشغيل يتم ضغطها وفقًا لـ Lorentz . في الفصل الأول ، يتم اشتقاق صيغة لموضع النقاط (GMT) المحيطة بنقطة معينة ، والتي لها نفس وقت التفاعل للحقول المادية. يتبين أن توقيت غرينتش هذا عبارة عن بيضاوي مضغوط وفقًا لـ Lorentz في اتجاه الحركة. دعونا الآن ننتبه إلى حقيقة أن حجم W لهذا البيضوي ينخفض بما يتناسب مع تقلص لورنتز. وينعكس هذا في الصيغة (1) أدناه. لنفترض الآن حقيقة رائعة أنه عندما يتم تسريع الجسم ، يتم إنفاق عمل القوة على ضغط حجم المساحة التي يشغلها، والتي بقيت بعد ذلك دون تغيير في حرية الحركة. على الأقل ، هذا الافتراض ليس أسوأ من المبدأ العلمي القائل بأن الفضاء يمكن أن ينحني أو يتضخم.
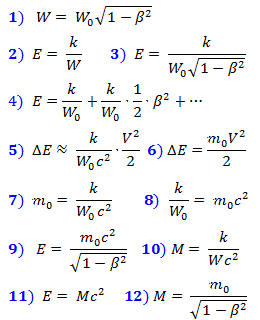افترض أن هذه الطاقة E تتناسب عكسيًا مع الحجم الذي كان من الممكن ضغطه وفقًا للصيغة (2) ، أو (3) بعد استبدال (1) فيه.
نقوم بتوسيع E من (3) إلى سلسلة Taylor (4) ، حيث (5) هي زيادة الطاقة من السرعة في التقريب الأول بسرعات منخفضة. ولكن بسرعات منخفضة يساوي أيضًا (6). بمقارنة (5) و (6) نحصل على (7) و (8). باستبدال (8) في (3) نحصل على (9) ، والتي تربط طاقة الجسم في الفضاء المضغوط بكتلة الراحة.
دعونا نعبر عن الكتلة النسبية بالصيغة (10) ، من حيث الاستبدال (2) ، نحصل على التعبير المعروف (11) ، الذي يربط الكتلة والطاقة. بمقارنة (9) و (11) نحصل على (12).
الكتلة هي مجرد صيغة أخرى للطاقة المستهلكة في ضغط الفضاء. وبهذا المعنى فهي متكافئة. والمادة فقط "تشير" إلى المساحة التي يشغلها الجسم.
التغير في الطاقة الإجمالية E للنظام ، أي طاقة الضغط للفضاء ، بما يتفق تمامًا مع الميكانيكا الكلاسيكية النيوتونية ، تساوي عمل القوة المطبقة كمنتج للقوة لكل مسار ، والتغيير في الزخم P للنظام يساوي منتج القوة نفسها ووقت عملها. تنعكس هذه التبعيات في الصيغ (13). بعد استبدالهم بعبارات الطاقة من (11) والزخم Pمن الصيغة (14)
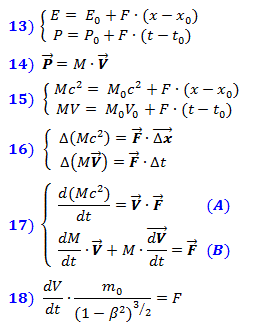نحصل على نظام المعادلات (15) ، المكتوب على شكل زيادات صغيرة في (16) في شكل متجه. ثم ، بالتمييز فيما يتعلق بالوقت ، نكتب نظام المعادلات التفاضلية (17) واصفا الديناميكيات النسبية. لا تحتاج القوة F إلى التمييز ، لأنها خارجية ولا تعتمد على اختلافات متغيرات النظام. باستبدال تعبير الكتلة من (12) في الصيغة ( أ ) ، نحصل على الصيغة النسبية المعروفة للحركة المستقيمة (18). 
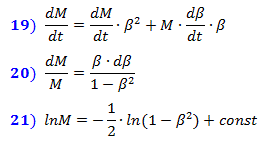من نظام المعادلات (17) من الممكن معرفة اعتماد الكتلة على السرعة. استبدال F من الصيغة ( B ) إلى الصيغة ( A ) وقسمة جانبي المساواة على c²، عند التسارع على طول مسار الحركة ، نحصل على التعبيرات (19) و (20). من حيث التكامل ، نحصل على تعبير (21). فمن السهل أن نرى أن ذلك يعادل التعبير لوغاريتمي (12) لكتلة النسبية، حيث CONST تساوي لوغاريتم بقية كتلة م 0 . هذا يعني أن مثل هذا الاعتماد للكتلة على السرعة يضمن توافق الطاقة Mc² والزخم M الخامس في الصيغ (16 ، 17). ومن هنا يتبع أيضًا أن القيمة التي افترضناها سابقًا ككتلة الباقية هي قيمة ثابتة مستقلة عن السرعة ، كما هو مكتوب في الصيغ الأصلية (9). وهذا يعني أن افتراضنا حول اعتماد الطاقة على درجة ضغط الفضاء صحيح.
بالطبع ، ادعاء ضغط الفضاء غير مقنع للغاية. إذا كان من المفترض أن يكون الفضاء عبارة عن حاوية فارغة من الجسيمات والأجسام ، فكيف يمكنك ضغط الفراغ؟ سيبقى الفراغ الفراغ. ومع ذلك ، يسمح العلم لنفسه بالحديث عن انحناء الفضاء الفارغ - تتطلب الصيغ ذلك. ومع ذلك ، بشكل دقيق ، فضاءه هو تجريد رياضي.
لكن يمكننا أن نفترض بشكل معقول إلى حد ما أن الفضاء ليس فارغًا ، ولكنه مليء بنوع من المادة ، التي نفترضها ، وليس في حالة مضغوطة ، على أنها فراغ.... عندما يكون ، على سبيل المثال ، تحت ضغط الضغط ، لدينا جسيمات وأجسام مادية. عندما تكون في حالة استراحة فيها ، فإن درجة الضغط (الطاقة) لقسم من هذه المادة تتوافق مع الكتلة المتبقية من الجسم ، ومع تسارعها ، تزداد درجة ضغط (الطاقة) للجسم والكتلة المقابلة.
وفي هذه البيئة المادية ، قد تتواجد الحقول المادية التي تحدد موقع الجسيمات وتفاعلها (حتى الجسيمات الأولية "جدًا" - التي نستمر في تخيلها ، وهي ظاهرة تركيز المجالات من بيئتها والتي بدونها لا وجود لها) ، وقد تنتشر بسرعة محددة ) ، يتم تحديد الباقي وطاقة الحركة من خلال درجة ضغط منطقة المادة الأولية التي يشغلونها . فعلا،تصف معادلات الديناميكيات النسبية فقط حركة عدم التجانس (الأجسام المادية) في المادة الأولية . كما نرى ، لا توجد تناقضات مع تجربة ميشيلسون وتحولات لورنتز.