فرز أسفل كومة الذاكرة المؤقتة

هذه هي المقالة الأخيرة في سلسلة فرز كومة الذاكرة المؤقتة. في المحاضرات السابقة ، نظرنا في مجموعة متنوعة من هياكل الكومة التي تظهر نتائج ممتازة من حيث السرعة. يطرح السؤال: ما هو نوع الكومة الأكثر فاعلية عندما يتعلق الأمر بالفرز؟ الجواب: هو الذي سننظر إليه اليوم.

EDISON .




— « » — -, CRM-, , iOS Android.



;-)

الأكوام الفاخرة التي نظرنا إليها سابقًا جيدة ، ولكن أكفأ كومة هي كومة الذاكرة المؤقتة القياسية مع تحسين التطهير.



ما هو المقاصة ، لماذا هو مطلوب في كومة وكيف يتم وصفه في الجزء الأول من سلسلة من المقالات.



تعمل عملية الغربلة القياسية في الفرز الكلاسيكي بواسطة مجموعة تقريبًا "الجبين" - يتم إرسال عنصر من جذر الشجرة الفرعية إلى الحافظة ، وترتفع عناصر الفرع ، وفقًا لنتائج المقارنة. كل شيء بسيط للغاية ، ولكن تبين الكثير من المقارنات.







في الممر التصاعدي ، يتم حفظ المقارنات نظرًا لحقيقة أنه لا يمكن مقارنة الآباء مع أحفادهم ، في الأساس ، يتم مقارنة المتحدرين فقط مع بعضهم البعض. في الكومة العادية ، تتم مقارنة الأصل مع المتحدرين ويتم مقارنة المتحدرين مع بعضهم البعض - وبالتالي ، فإن المقارنات تزيد تقريبًا مرة ونصف مع نفس عدد التبادلات.



لذا كيف يعمل ، دعنا نلقي نظرة على مثال محدد. لنفترض أن لدينا مصفوفة تكونت فيها كومة الذاكرة المؤقتة بالفعل - كل ما تبقى هو غربلة الجذر. بالنسبة لجميع العقد الأخرى ، يتم استيفاء الشرط - أي طفل ليس أكبر من والديه.



بادئ ذي بدء ، من العقدة التي يتم إجراء المقاصة لها ، تحتاج إلى النزول على طول الأحفاد الكبيرة. حفنة من ثنائي - أي لدينا سليل يسار وسليل يمين. ننزل إلى الفرع حيث يكون السليل أكبر. في هذه المرحلة ، يحدث العدد الرئيسي من المقارنات - تتم مقارنة الأطفال الأيسر / الأيمن مع بعضهم البعض.







بعد أن وصلنا إلى الورقة في المستوى الأخير ، قررنا بالتالي الفرع الذي تحتاج إلى تحويل القيم لأعلى. لكنك لست بحاجة إلى نقل الفرع بأكمله ، ولكن فقط الجزء الأكبر من الجذر الذي بدأت منه.



لذلك ، نذهب إلى الفرع لأعلى عقدة ، وهي أكبر من الجذر.







الخطوة الأخيرة هي استخدام متغير المخزن المؤقت لتحريك قيم العقدة إلى أعلى الفرع.







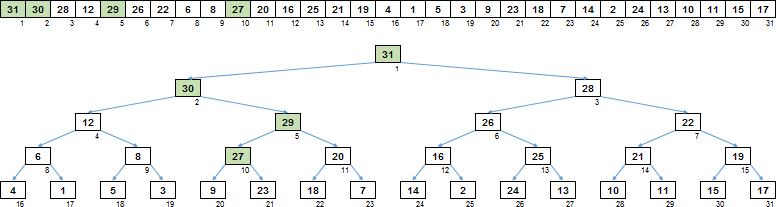
هذا هو. شكلت المقاصة الصاعدة شجرة فرز من مصفوفة ، حيث يكون أي والد أكبر من نسله.



الرسوم المتحركة النهائية:

بايثون 3.7 التنفيذ

لا تختلف خوارزمية الفرز الأساسية عن heapsort المعتاد:

#    
def HeapSortBottomUp(data):

    #    
    #   -   
    # (   )       
    for start in range((len(data) - 2) // 2, -1, -1):
        HeapSortBottomUp_Sift(data, start, len(data) - 1) 

    #        
    #        .
    for end in range(len(data) - 1, 0, -1): 
        #       
        #    
        data[end], data[0] = data[0], data[end]
        #        
        #   
        #     
        HeapSortBottomUp_Sift(data, 0, end - 1)
    return data

يتم النزول إلى الورقة السفلية بشكل ملائم / بصري في وظيفة منفصلة:

#      
#   
def HeapSortBottomUp_LeafSearch(data, start, end):
    
    current = start
    
    #  ,  
    #  (  ) 
    while True:
        child = current * 2 + 1 #  
        #  ,    
        if child + 1 > end: 
            break 
        #  ,   
        if data[child + 1] > data[child]:
            current = child + 1
        else:
            current = child
    
    #  ,    
    child = current * 2 + 1 #  
    if child <= end:
        current = child
        
    return current

والأهم من ذلك - الفسحة ، النزول أولاً ، ثم الظهور:

#  
def HeapSortBottomUp_Sift(data, start, end):
    
    #        
    current = HeapSortBottomUp_LeafSearch(data, start, end)
    
    #  ,    
    #     
    while data[start] > data[current]:
        current = (current - 1) // 2
    
    #   ,
    #      
    temp = data[current]
    data[current] = data[start]
    
    #        
    # -     
    while current > start:
        current = (current - 1) // 2
        temp, data[current] = data[current], temp  

تجريبيًا بحتًا - وفقًا للقياسات الخاصة بي ، يعمل التصنيف التصاعدي بواسطة كومة الذاكرة المؤقتة 1.5 مرة أسرع من الفرز العادي بواسطة كومة الذاكرة المؤقتة.



وفقًا لبعض المعلومات (على صفحة الخوارزمية في ويكيبيديا ، في ملف PDF الذي تم الاستشهاد به في قسم "الروابط") ، فإن BottomUp HeapSort في المتوسط ​​قبل الفرز السريع - للمصفوفات الكبيرة إلى حد ما من 16 ألف عنصر أو أكثر.

الروابط

heapsort من أسفل إلى أعلى



A متغير من Heapsort مع العدد الأمثل تقريبًا من المقارنات



بناء كومة



الذاكرة المؤقتة نوع جديد من ضربات heapsort ، في المتوسط ​​، فرز سريع (إذا لم يكن n صغيرًا جدًا)

مقالات سلسلة:

• تطبيق Excel AlgoLab.xlsm
• أنواع التبادل
• أنواع الإدراج
• فرز التحديد
  • أنواع الكومة: N-Pyramids
  • أنواع الكومة: أرقام ليوناردو
  • أنواع الكومة: كومة ضعيفة
  • أنواع الكومة: شجرة ديكارتية
  • أنواع الكومة: شجرة البطولة
  • فرز كومة الذاكرة المؤقتة: تصاعدي تصاعدي
• دمج الأنواع
• فرز التوزيع
• الفرز الهجين

تمت إضافة تصنيف اليوم إلى تطبيق AlgoLab الذي يستخدمه - قم بتحديث ملف excel باستخدام وحدات الماكرو.